RESS论文 | 用于轴承剩余使用寿命预测的双通道动态样条图卷积网络
本期给大家推荐一篇发表于高分期刊RESS的剩余寿命预测领域相关文章:用于轴承剩余使用寿命预测的双通道动态样条图卷积网络。针对传统方法难以捕捉振动数据中的动态拓扑变化和非线性退化规律的问题,文章提出双通道动态样条图卷积网络剩余寿命预测模型。该模型通过整合全局拓扑建模的GCN、连续局部特征演化的SplineCNN以及时序依赖分析的GRU,有效捕捉轴承振动信号中的时空退化特征,为轴承剩余使用寿命预测提供了可靠解决方案。
论文链接:通过点击本文左下角的阅读原文进行在线阅读及下载。
论文基本信息
论文题目:
Dual-channel dynamic spline graph convolutional network for bearing remaining useful life prediction
论文期刊:Reliability Engineering and System Safety
论文日期:2025
论文链接:
https://doi.org/10.1016/j.ress.2025.111731
作者:Yubei Jin (a), Dongdong Liu (a), Yongchang Xiao (a), Lingli Cui (b)
机构:
a: Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100124, China;
b: Beijing Engineering Research Center of Precision Measurement Technology and Instruments, Beijing University of Technology, Beijing 100124, China.
通讯作者邮箱:
cuilingli@bjut.edu.cn
作者简介:
崔玲丽,教授,博士生导师。2008年入选“北京市科技新星计划”,2008年获冶金部科技进步二等奖,2009年入选国家留学基金委的访问学者全额资助计划,2010年入选“北京市中青年骨干教师计划”,2011年9月至2013年4月于美国密歇根大学访学,2013年入选北京工业大学“国际化导师能力发展计划”,2015年入选北京工业大学“首批青百人才计划”,2016年入选国家人社部及北京市人社部“留学人员科技活动项目择优资助计划”,2017年入选“北京市长城学者”计划,2018年入选“北京市百千万人才”计划。2018年获“中国振动工程学会青年科技奖”及第二十一届“茅以升北京青年科技奖”。作为项目负责人主持国家自然科学基金项目3项,获ICFDM2016十佳优秀结题项目,作为骨干成员参加了国家863科技计划项目以及企业横向项目等多项课题。至今发表SCI及EI检索学术论文40余篇,获批国家发明专利16余项。(来自学校官网)
目录
摘要
1.引言
2.基础理论
2.1.图卷积网络
2.2.基于样条的卷积神经网络
3.提出的方法
3.1.双通道图卷积网络
3.2.DSAF
3.2.1.动态激活函数
3.2.2.DSAF:注意力累积分割
3.2.3.梯度导数
3.3.损失函数设计
4.实验验证与分析
4.1.数据预处理
4.1.1.数据标准化
4.1.2.图形结构构建和标签设置
4.2.评估与讨论
4.2.1.实验数据集说明
4.2.2.案例研究一:PHM 2012挑战数据集
4.2.3.案例研究二:XJTU-SY轴承数据集
4.2.4.复杂性与性能权衡分析
4.2.5.消融实验分析
4.2.6.超参数敏感性分析
4.2.7.模型方差分析
4.2.8.收敛性分析
4.2.9.样条核参数与边缘属性的灵敏度分析
5.结论
摘要
在工业系统预测性维护中,准确预测轴承剩余使用寿命(Remaining Useful Life, RUL)至关重要。然而传统方法往往难以捕捉振动数据中的动态拓扑变化和非线性退化规律。为解决这一难题,我们提出双通道动态样条图卷积网络(Dual-Channel Dynamic Spline Graph Convolutional Network, DDSGNet)。与依赖离散特征聚合的传统方法不同,本文通过全局拓扑聚合模块建模振动特征的空间相关性。连续局部演化算子捕捉静态退化的动态特征,而时间依赖学习器则保留长距离序列信息。该方法有效解决了连续局部特征变化建模的难题。创新性地提出DSAF激活函数,通过平滑梯度动态适应非线性信号变化,有效解决了梯度粗糙和梯度消失问题。同时引入基于物理约束的PhyMAE损失函数,精准匹配轴承退化特性,确保预测结果既准确又符合物理规律。实验表明,DDSGNet在两个公开数据集上的表现优于现有最优方法,为轴承剩余使用寿命预测提供了可靠解决方案。
关键词:剩余使用寿命,全局拓扑聚合,局部演化算子,物理引导的损失函数
1 引言
在预测性健康管理(Predictive Health Management, PHM)[1]领域,剩余使用寿命(Remaining Useful Life, RUL)预测是一项关键且具有挑战性的任务,因其直接影响机械系统的可靠性和维护。轴承作为旋转机械[2]的核心部件,广泛应用于电机及航空航天设备中,其核心作用在于支撑旋转轴并降低摩擦损耗。然而,长时间运行会使轴承承受机械应力、热应力、润滑条件变化及环境影响等多重考验,这些因素共同导致性能下降,最终引发故障。研究表明,轴承故障在旋转机械故障中占比显著[3,4],不仅会降低运行效率,还可能带来严重安全隐患。因此,精准的轴承寿命预测技术不仅能保障设备稳定运行,还能持续提升效率并增强安全性[5-7]。
工业自动化技术的进步推动了对轴承(RUL)精准预测的需求,以确保设备稳定可靠运行。传统RUL预测方法包含模型驱动和数据驱动两大类[8]。然而,依赖预设公式和经验的模型驱动方法,由于适应性有限,在复杂工况下难以准确捕捉设备退化过程。随着现代机械设备振动数据的大量涌现,数据驱动方法特别是深度学习(Deep Learning, DL)应运而生——这种技术在信号处理和模式识别领域展现出卓越优势[9-12]。通过直接从振动数据中建模退化模式,这些方法具备强大的适应性和泛化能力,使得数据驱动的剩余使用寿命预测成为当前研究的热点领域。
基于数据的轴承剩余使用寿命预测方法可分为传统机器学习技术和深度学习方法两大类。传统机器学习方法如支持向量机[13]和隐马尔可夫模型[14]虽能处理复杂数据集,但需要人工特征工程依赖领域专业知识,导致其难以自动适应并从复杂振动信号中提取特征。相比之下,深度学习模型凭借强大的特征提取与拟合能力备受关注。近年来,深度学习方法已成为预测与分类领域的研究热点[15,16]。例如,Jonug等人[17]采用了一种深度学习模型,该模型整合了LSTM和RNN技术用于检测轴承中的异常。该模型既能保持长期依赖关系,又能识别局部依赖关系。Wu等人[18]将希尔伯特变换与自动编码器相结合,有效提升了RUL预测的准确性。此外,这种方法在利用希尔伯特变换评估劣化阶段和识别劣化因素时,为提升可解释性提供了新的可能。Li等人[19]采用GRU网络结合趋势记忆注意力机制,成功预测了轴承的剩余使用寿命。曹等人[20]创新性地将并行GRU与双层注意力框架相结合,实现了轴承剩余寿命的精准预测。Huang等人[21]则开发了双向长短期记忆(Bidirectional Long Short-Term Memory, BiLSTM)模型,通过整合传感器数据与运行状态信号,显著提升了剩余寿命预测的准确性。尽管这些方法在时间序列建模和捕捉长期依赖关系方面表现优异,但在处理空间相关性时仍存在局限,这直接影响了其对空间关系的表征能力。
为有效利用轴承振动信号中的空间特征与局部关联性,研究者尝试将卷积神经网络(Convolutional Neural NetworkCNN)与RNN相结合,用于预测轴承RUL。Dao等人[22]通过结合CNN和LSTM对机械设备进行故障诊断。Al Dulaimi等人[23]采用双路径预测RUL:LSTM路径提取时间特征,CNN路径提取空间特征。Wang等人[24]提出循环卷积神经网络(Recurrent Convolutional Neural Network, RCNN)架构,有效捕捉CNN的时间依赖特性。Gao等人[25]同时运用一维卷积神经网络(One-Dimensional Convolutional Neural Network1D CNN)和BiLSTM,在卷积层中引入ELU激活函数,构建混合神经网络模型以提升预测精度和稳定性。Liu等人[26]分别通过BiLSTM和CNN从序列数据中提取长期时间依赖特征和关键局部特征。然而这些方法忽视了退化数据中固有的拓扑关系,未能充分挖掘其结构信息。
作为新型深度学习架构,图神经网络(Graph Neural Networks GNNs)为解决上述问题提供了新思路。图数据通过节点和边缘表征了劣化数据间的拓扑关系,为复杂建模奠定了基础。GNNs能够高效处理图数据并捕捉节点间的复杂关联,这对建模轴承监测数据中的传感器相关性及运行状态变化具有重要意义。在轴承RUL预测中,GNNs可将传感器数据和运行状态视为退化数据图中的节点和边缘,通过学习节点间的动态交互实现更精准的寿命预测。Wei等人[27]将注意力机制与GCN相结合,有效提升了预测性能。Yang等人[28]提出节点层级路径图模型,用于捕捉节点相关性的时间依赖特性,并设计了结合BiLSTM的ChebGCN。Wang等人[29]开发了门控图卷积网络,通过整合门控循环单元(GRU)和图卷积网络(Graph Convolutional Network, GCN),能够同步挖掘传感器数据中的时空信息,实现RUL预测。Wei等人[30]提出自适应图卷积网络,该网络能动态选择合适图结构并集成自适应调节机制,有效揭示不同节点特征间的复杂关联,从而精准预测轴承的剩余使用寿命。Jiang等人[31]整合多层级加权混合邻域信息,通过构建多层次图表示模块分析传感器空间关系,并结合BiLSTM模拟传感器数据中的时序动态特征。Li等人[32]提出分层注意力图卷积网络(Hierarchical Attention Graph Convolution Network, HAGCN),采用分层图表示模块分析传感器空间关系,并通过BiLSTM模拟传感器数据的时序动态特征。He等人[33]将自回归移动平均滤波器(Autoregressive Moving Average filter, ARMA)引入GCN,有效解决了传统GCN在动态拓扑数据中出现的过度平滑问题。Cui等人[34]提出了一种结合稀疏图结构整合的卷积网络,通过端到端方法显著提升了机器预测轴承RU)的准确性。Xiao等人[35]的研究创新性地构建了图神经网络架构,采用异构图表示技术实现多重数据聚合,专门用于轴承RUL预测。Jiang等人[36]运用图标特征迁移方法,构建了由两个不同拓扑图组成的双图结构。该方法充分挖掘有限标注样本中的信息,有效捕捉节点间更丰富的拓扑结构特征。
尽管上述方法在RUL预测中表现出色,但仍存在明显不足。首先,传统GCN方法依赖拓扑邻接关系进行特征聚合,无法持续捕捉节点局部邻域的特征变化趋势。其次,轴承退化过程受多种因素影响,其特征表达具有高度非线性和动态性,传统激活函数和模型架构难以适应这种复杂变化。
为突破现有局限,我们提出创新框架DDSGNet,通过整合全局拓扑建模、连续局部特征演化与时序依赖分析,从根本上提升轴承RUL预测能力。与难以建模连续局部特征变化的传统GCN模型,以及忽视拓扑关系的CNN-LSTM混合模型不同,DDSGNet采用双通道图学习机制,将全局拓扑聚合与连续局部演化相结合,成功捕捉离散图卷积或传统CNN方法难以建模的多尺度时空退化规律。创新性地引入具有平滑梯度的DSAF激活函数,动态适应非线性信号变化,显著超越ReLU或DReLU等静态激活函数。同时引入PhyMAE物理约束模块,通过单调性和非负性等轴承特性约束,确保预测结果符合退化物理规律,突破传统通用损失函数的局限。这种协同设计使DDSGNet在精度与鲁棒性方面实现质的飞跃。主要贡献包括:
(1) 构建了一个双通道图卷积网络,该网络将全局拓扑建模的GCN优势与连续变化建模的样条CNN能力有机结合。通过充分挖掘图结构数据、时空特征及时间序列信息,实现了轴承振动信号的多模态特征融合。该方法不仅深入揭示了轴承性退化规律,还能为预测RUL提供更详尽的特征集。
(2)提出动态平滑激活函数(Dynamic Smooth Activation Function, DSAF),通过动态调整激活参数来增强传统激活函数在设备退化建模中的适应性,从而更精准捕捉信号的非线性特征。同时,该函数的平滑特性与非单调行为被有效利用,显著提升了模型的训练效率和预测性能。
(3)引入了物理约束损失函数PhyMAE,将轴承退化过程固有的单调性和非负性作为模型训练的先验知识。确保了模型预测结果更符合轴承退化规律。
本文后续章节结构安排如下:第二章阐述本研究的基础理论;第三章详细说明提出的方法;第四章全面介绍实验设置与数据集,并通过结果分析验证方法有效性;第五章总结研究方法与结论。
2 基础理论
2.1 图卷积神经网络
GCN是一种用于建模图数据中拓扑结构和节点关系的先进卷积范式,其信息传播基于图的拓扑结构和节点特征,在节点分类、图学习和表示方面发挥着重要作用,GCN的核心公式如下:
其中 表示第 层的节点特征矩阵。 是添加自环的邻接矩阵,确保每个节点都能保留自身特征。 是 的度矩阵,该矩阵本身是对角矩阵,每个元素代表对应行的度数。 是第 层的可训练参数矩阵。 是激活函数。通过归一化操作 ,确保信息在传递过程中保持一致性,从而避免因节点度数差异导致的梯度消失或爆炸现象。
GCN算法具备强大的全局特征建模能力,通过聚合邻近节点信息来学习全局图拓扑结构。然而,该算法主要依赖图的拓扑连接进行信息传播,缺乏对节点局部邻域特征连续变化趋势的建模能力,难以捕捉节点间细微但关键的局部演化特征。因此,在需要捕捉局部退化模式的任务中(如轴承剩余使用寿命预测),该算法存在局限性。为克服这一缺陷,我们引入了互补的局部演化算子,确保局部退化动态能够得到连续建模。
2.2.基于样条的卷积神经网络
SplineCNN是一种专为图数据设计的卷积神经网络。其核心优势在于采用B样条核函数,在图结构中实现连续可微的局部卷积操作,从而提供更灵活且可学习的特征提取能力。与传统图卷积网络仅基于邻接矩阵聚合离散邻域特征不同,SplineCNN通过结合节点局部邻域信息与边属性,能够模拟节点特征随空间关系变化的连续演变模式。具体而言,该网络利用基于B样条基函数的核函数,对节点间边属性进行连续插值,从而建立节点间的连续特征映射关系。这种连续建模方法不仅克服了传统GCN在特征聚合过程中产生的离散化误差,还能在端到端训练过程中自适应学习局部特征随空间变化的平滑演变趋势,无需显式设计或人工提取几何特征[37],因此具有更强的自动建模能力。SplineCNN的信息传播过程如下:
其中 表示边属性, 是基于B样条的权重矩阵,其计算方式如下:
其中 表示d阶B样条基函数, 是节点向量,用于定义基函数的支持区间。由于B样条核的数学特性,其在SplineCNN中的应用特别适合用于轴承剩余使用寿命预测。通过递归基函数(公式(5))定义的B样条核具有局部支持特性,即仅在有限区间内非零,并且具有连续可微性。这使得节点间边缘属性的平滑插值成为可能。因此,SplineCNN能够模拟振动信号特征在空间关系中的连续演变,捕捉随时间和空间平滑变化的细微劣化趋势。B样条核参数化连续特征过渡的能力确保了对局部邻域动态的精确建模,这对准确预测轴承RUL至关重要。
3 提出的方法
本文针对传统方法在捕捉轴承振动信号中复杂空间拓扑与时间退化模式方面的局限性,提出了一种双通道图卷积网络。所提出的DDSGNet巧妙融合空间拓扑与时间退化建模,有效应对轴承RUL预测的关键挑战。为精准提取振动信号中的拓扑特征与动态特征,创新性地设计了GCN和SplineCNN双通道架构。针对时间依赖性捕捉难题,引入GRU模块对融合特征进行智能处理。为提升非线性退化模式建模精度并确保物理一致性,提出动态平滑激活函数(Dynamic Smooth Activation Function, DSAF)优化模式特征,同时采用物理引导损失函数(Physical-Guided Loss Function, PhyMAE)保持物理一致性,最终实现高精度的剩余使用寿命预测。具体技术细节如下所述。
3.1.双通道图卷积网络
DDSGNet中的双通道图卷积网络通过GCN与SplineCNN的协同组合实现了理论突破。与传统GCN通过邻接矩阵聚合离散邻域特征、难以捕捉特征平滑过渡的局限不同,SplineCNN采用B样条核建模局部邻域内特征的连续演变。这种创新设计有效降低了离散化误差,显著提升了对轴承振动信号中细微劣化模式的识别能力。双通道架构使DDSGNet能够表征多尺度时空劣化模式,这对精准预测RUL至关重要,其性能超越了仅关注全局拓扑或时域动态的传统方法。具体实现流程如下:
输入的特征矩阵和邻接矩阵首先经过图卷积层处理,GCN层通过聚合节点的邻域信息,并利用学习到的权重更新节点特征,从而逐步建模图的结构特征。这一过程能有效捕捉图中的全局关联信息,为后续特征融合奠定基础。
随后,特征矩阵 和边属性 被输入到样条卷积网络层,该层通过B样条基函数建模节点间的空间关系。
其中 表示节点 与节点 之间的边属性,而基于B样条基函数的连续卷积核 用于根据边属性 计算节点 对节点 的贡献权重。其定义如下:
其中 表示B样条基函数的笛卡尔积, 代表可训练控制点的权重, 是B样条基函数的取值。经过样条卷积层处理后,可获得局部连续变化特征 。通过将GCN层提取的全局特征与样条卷积层提取的局部连续变化特征进行融合,充分发挥二者互补优势。具体公式如下:
其中 和 是全连接层的权重矩阵,分别用于处理全局特征和局部特征。融合后的特征 最终通过最后一个全连接层进行处理,生成最终输出。
3.2. DSAF
DSAF在动态ReLU(Dynamic ReLU, DReLU)基础上进行改进,旨在提升轴承RUL预测的非线性特征拟合能力(见图1和图2)。DReLU最初作为动态激活机制被提出,通过分割输入特征来捕捉多样化的退化模式,但存在梯度不平滑的问题。DSAF通过将分段注意力机制与平滑的非单调Swish函数相结合,有效解决了这一问题,不仅提升了训练稳定性,还避免了梯度消失现象。本节首先概述DReLU的工作原理,接着详细阐述DSAF的改进方案,并给出其数学定义及梯度分析。
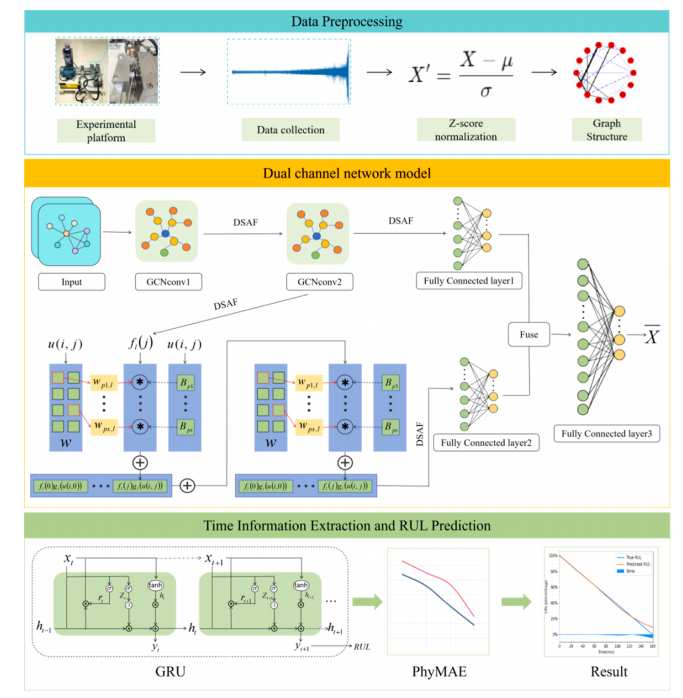
图1 基于所提出的方法进行RUL预测的框架
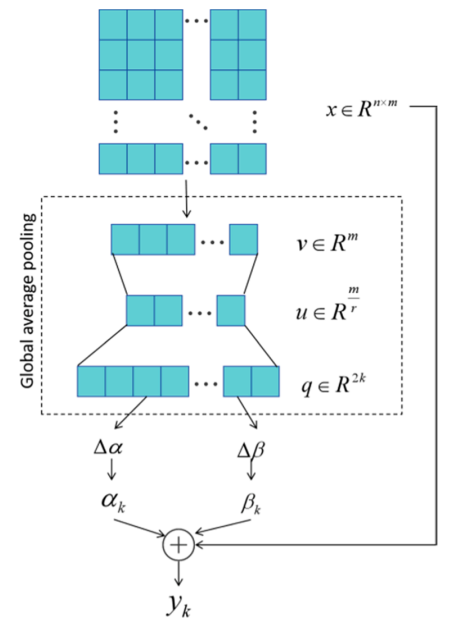
图2 DReLU的结构
3.2.1.动态激活函数
DReLU是一种自适应激活函数,能够根据输入信号动态调整激活参数,从而更精准地捕捉信号中的非线性特征[38]。如图3所示,输入张量 (其中 为样本数量, 为特征数量),通过全局平均和池化处理,最终得到全局信息向量 。
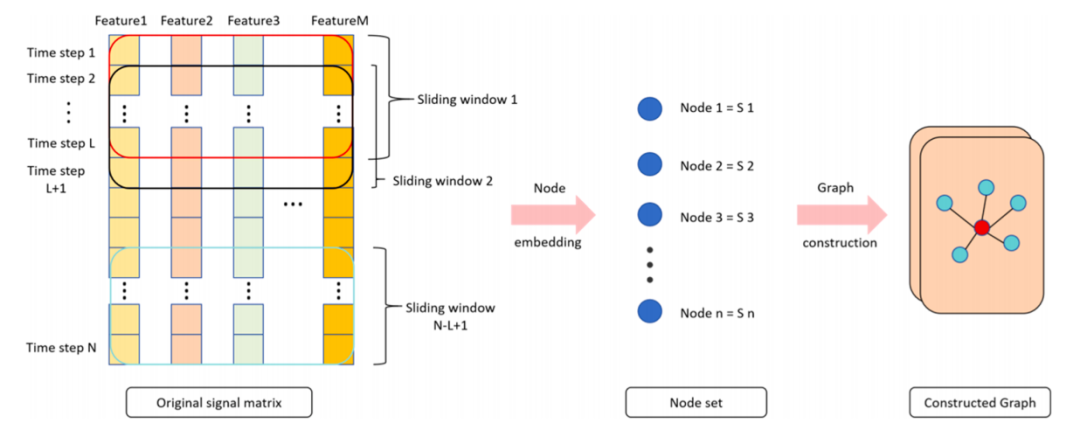
图3 图构建过程
全局信息向量通过全连接层FC1压缩得到 ,其中 为压缩比。再通过全连接层FC2恢复维度,并分割为 个分段参数 ,其中 为分段数量。
被划分为两部分,分别对应 和 。根据超参数 和 以及初始参数 和 ,最终的参数值 和 可计算得出:
为增强响应并捕捉关键特征,需计算每个输入元素的分段线性函数值,并选取最大值:
“动态门控+最大响应”的激活模式不仅能增强对关键特征的响应,还能提升对输入非线性结构变化的适应能力。
3.2.2.DSAF:注意力累积分割
DReLU通过计算所有分段的最大值作为最终输出。这种方法能增强响应效果,在特定场景下捕捉最强特征,但可能忽略其他潜在有用的特征分割信息。此外,DReLU的非平滑特性会导致梯度在不同分段边界处突然变化,从而引发训练不稳定。为解决这些问题,我们通过引入全自注意力机制并搭配Swish激活函数,对DSAF进行了重构。这种改进使模型既能选择性关注退化相关模式,又能保持梯度平滑性。DSAF的数学表达式定义为:
其中, 表示分配给第 个片段的注意力权重,其计算方式为:
其中 和 是可学习的矩阵,而分母 则用于稳定注意力分数。 输出通过Swish激活函数传递:
这种设计引入了平滑且非单调的非线性特性,显著提升了优化过程的稳定性。为确保DSAF模型在分割任务中实现精准特征捕捉,我们将分割数量 设定为4,以此平衡模型复杂度与非线性特征表征的精细度。该参数通过验证集的实证调优确定, 4既能保证最佳预测精度又避免过拟合问题。全连接层FC1的压缩比 设为8,既能有效降低全局信息向量的维度,又能保留关键信号特征。针对Swish函数,其可学习参数 β
3.2.3 梯度导数
为评估优化特性,我们推导DSAF关于 的梯度。设:
然后,第 个输出相对于 的偏导数为:
Swish段梯度:
由于Swish函数具有可微性,该梯度是平滑且有界的。 累积注意力梯度:
复合梯度 具有Lipschitz连续性,因为Swish和softmax函数均可微且导数有界。此外,采用带有注意力加权的累积分割技术,可有效缓解ReLU函数的不平滑特性以及Sigmoid函数的梯度消失问题。
3.3.损失函数设计
损失函数是深度学习模型训练过程的核心要素。它通过量化模型预测值与实际值之间的差异,来引导模型优化路径。平均绝对误差(Mean Absolute Error, MAE)作为基础损失函数:
其中 为真实值, 为预测值, 为样本总数。该损失函数在多数回归任务中表现良好,但在轴承RUL预测中,可能未能充分考虑轴承退化的实际物理规律,导致预测结果不合理。
为使预测结果更准确反映轴承RUL的物理规律,本文在损失函数中引入单调性和非负性约束,构建了物理引导损失函数PhyMAE,从而提升预测结果的准确性和可解释性。具体实现如下:
轴承的RUL应随时间 单调递减: 。因此,我们将单调性约束条件表述为:
该模型能确保最终预测值随时间推移呈单调递减趋势。若不符合此特性,系统将对模型施加惩罚机制,促使模型学习合理的退化轨迹。
轴承的RUL应为非负值: 。我们将非负约束条件表述为:
该模型用于确保最终预测值为非负值,同样地,若未满足该特性,模型将受到惩罚以进一步增强物理一致性。基于上述基本损失函数和物理约束条件,本文最终提出的损失函数可表示为:
其中 代表权重因子,用于平衡各项参数。本文采用ReLoBRaLo方案[39]来调节 的数值。该方案通过动态调整权重因子 ,平衡MAE与PhyMAE损失函数中的物理约束条件(非负性和单调性)。具体而言,ReLoBRaLo在训练过程中实时监测MAE与约束损失项的相对权重,当物理约束违反显著时增加 ,当MAE占主导时降低 。初始 值设定为0.5,取值范围[0.1,1.0],通过在XJTU-SY数据集上的经验调参确定,既保证预测精度又确保物理一致性。这种自适应调节机制稳定了训练过程,同时增强了模型与轴承劣化物理规律的匹配度。通过调整这些超参数的数值,可控制损失函数中各项的贡献比例,从而优化模型性能并提升轴承剩余使用寿命预测的准确性。
PhyMAE的收敛性通过与Adam优化器的集成得以保障,该优化器采用自适应矩估计技术实现稳定的梯度下降。从数学角度而言,由于惩罚项具有分段线性特征,PhyMAE相对于预测值的梯度定义明确,从而确保优化过程的平滑性。损失函数的Lipschitz连续性(由MAE和ReLU惩罚项产生的有界梯度所保证)在权重和学习率有界的标准假设下,确保了算法的收敛性。
4 实验验证与分析
本节对所提出的方案进行评估和讨论,实验采用两个真实故障场景数据集,通过与多种前沿方法的对比验证了该方案的有效性。
4.1.数据预处理
4.1.1.数据标准化
公开轴承数据集中的传感器信号在不同工况和老化阶段存在显著的幅值波动。若直接使用原始数据进行分析,可能导致忽略信号微弱特征,进而影响神经网络的收敛效果。为此,我们采用Z分数标准化方法对数据分布进行缩放,并统一各维度的量纲。 Z分数标准化是数据标准化的常用方法,通过将数据转换为均值为0、标准差为1的分布,消除不同特征间的维度差异和数据偏斜。具体而言,对于每个特征 ,其标准化值 可表示为:
其中 为特征均值, 为特征标准差。通过Z分数标准化,所有特征均被统一到同一尺度,从而提升模型的训练效率和预测性能。
4.1.2.图结构构建与标签设置
图3展示了图结构的构建过程。首先,我们采用滑动窗口技术对时间序列进行分段处理。具体来说,设置长度为10的窗口,并以1为步长在时间序列上滑动。每个窗口捕获的数据段被定义为图中的一个节点。在获得节点集 合后,我们使用KNN方法构建图结构。对于每个数据点 ,计算其与所有其他数据点的欧氏距离。假设数据集包含 个样本,每个数据点 是一个D维向量,欧氏距离可表示为:
根据计算距离,为每个数据点选取最近的K个邻近点,得到集 合
为提高轴承RUL预测精度,采用轴承剩余使用寿命百分比作为标签。信号样本的标签设置如下:
其中
4.2.评估和讨论
4.2.1.实验数据集描述
本研究采用公开的XJTU-SY轴承数据集[40]和PHM2012挑战数据集[41]进行实验验证,这两个数据集均源自加速老化实验,属于真实运行故障数据。
XJTU-SY数据集是由西安交通大学(XJTU)和浙江昌兴益阳科技有限公司(SY)联合发起的项目,为轴承研究提供了全面的资源。如图4所示,实验装置包含交流电机、旋转轴、速度控制单元、液压加载机构、支撑轴承以及测试轴承本身。该平台支持在不同运行场景下对滚动轴承进行加速老化测试,并收集大量生命周期数据。关键可调参数包括由液压系统作用于测试轴承壳体产生的径向载荷,以及通过交流电机控制器调节的转速。

图4 XJTU-SY 实验平台
为完整记录轴承的振动信号全生命周期,我们采用磁性基座将两个PCB352C33单向加速度传感器分别安装在测试轴承的水平轴和垂直轴上。实验中使用DT9837便携式动态信号采集器进行振动信号采集,采样参数设置为:采样频率25.6千赫兹、采样间隔1分钟、每次采样持续1.28秒。当振动信号振幅超过初始值十倍时,表明轴承已完全停止工作,此时终止测试。由于载荷作用方向为水平,该平面的振动信号能更直观地反映劣化过程。本文采用水平振动信号进行分析研究。 该研究包含15组滚动轴承在三种不同工况下的全生命周期退化数据,数据分为训练集和测试集,分别用于模型训练和最终预测的准确性评估。表1展示了XJTU-SY的运行参数。
表1 XJTU-SY 的运行参数

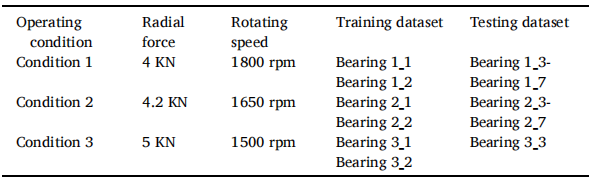
图5展示了预测实验平台,该平台是公共PHM2012数据集的来源。该装置由电机驱动,用于调节测试轴承的转速。编码器提供实时速度测量数据,支持反馈调节。为加速轴承磨损,可通过负载调节系统在测试轴承上施加可定制的径向力。该振动传感器由两个呈90度角排列的微型加速度计组成,分别安装在垂直轴和水平轴上。两个加速度计沿轴承外圈径向分布,以25.6千赫的采样率工作。位于外圈附近孔洞内的电阻温度检测器,以0.1赫兹的频率记录温度数据。当振动幅值超过20g时,实验即告终止,标志着轴承完全失效。该数据集包含17种滚动轴承的生命周期退化曲线,这些数据是在三种不同工况下采集的,具体参数详见表2。
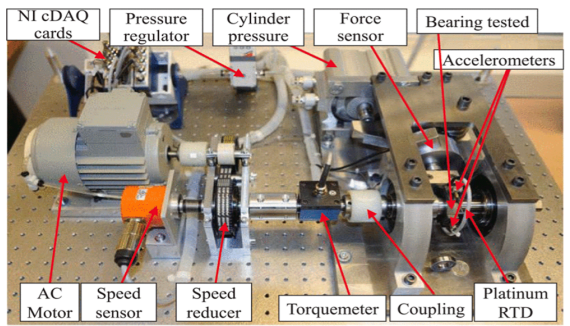
图5 PRONOSTIA实验平台
表2 PHM2012数据集操作条件的详细信息
4.2.2.案例研究一:PHM 2012挑战数据集
本研究采用公开的PHM2012挑战数据集,对所提方法的性能进行评估。具体实验设置详见表3。为验证该方法的有效性,我们进行了五组实验。评估指标包括均方根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)和相关系数(Correlation Coefficient, R²),具体说明如下:
其中
表3 PHM2012数据集的实验设置

为验证所提方法的有效性,我们将其与多项先进预测方法进行对比。TCN-GRU[42]融合了时间卷积网络的并行计算能力与门控循环单元的强大学习能力,并整合了注意力机制。CTLS[43]则通过整合卷积神经网络、Transformer、神经网络架构(LSTM)以及平滑半鞅随机层,显著提升了RUL预测的准确性。
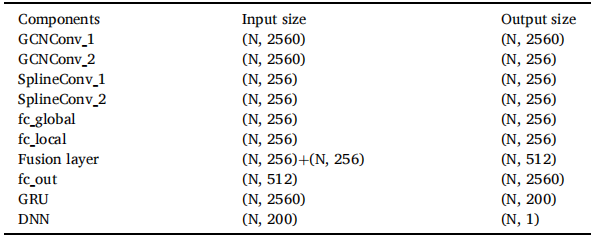
GAE[44]提出了一种基于图的框架,该框架将时间序列数据转换为图结构,并利用图自动编码器(GAE)、图注意力网络(GAT)和Transformer编码器进行处理。本方法采用Adam优化器,学习率设为0.001,训练周期为200个epoch。为确保实验可复现性,所有实验均使用固定随机种子42进行初始化。具体架构与参数设置详见表4,其中
表4 提出模型的结构
通过将MAE、RMSE和R²指标与其他方法进行对比,我们评估了所提方法的有效性,如表5所示。实验结果表明,该方法具有显著的精度优势。以轴承1-3为例,该方法的RMSE值为0.0271,MAE值为0.0195,R²值达到0.9912,相较于TCNGRU和CTLS方法有显著提升,这表明模型在追踪退化模式时展现出更强的适应能力。在轴承2-4的测试中,该方法表现尤为突出,其R²值高达0.9944,RMSE和MAE分别降至0.0216和0.0177,远优于CTLS和GAE方法,充分体现了模型卓越的建模能力。图6展示了轴承1-3、1-4、2-4、2-7和3-3的线性退化指标预测轨迹及误差指标。显然,所提出的方法能有效追踪退化模式。图7和图8对比分析了所提出方法与替代方法的RMSE和MAE指标。数据显示,该方法的预测误差普遍最小,证明了其有效性。
表5 所提出的方法与其他方法的性能比较
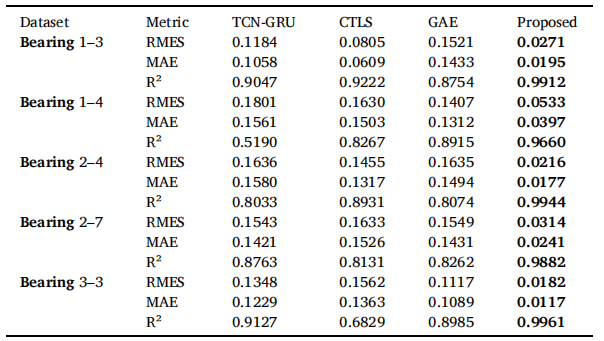
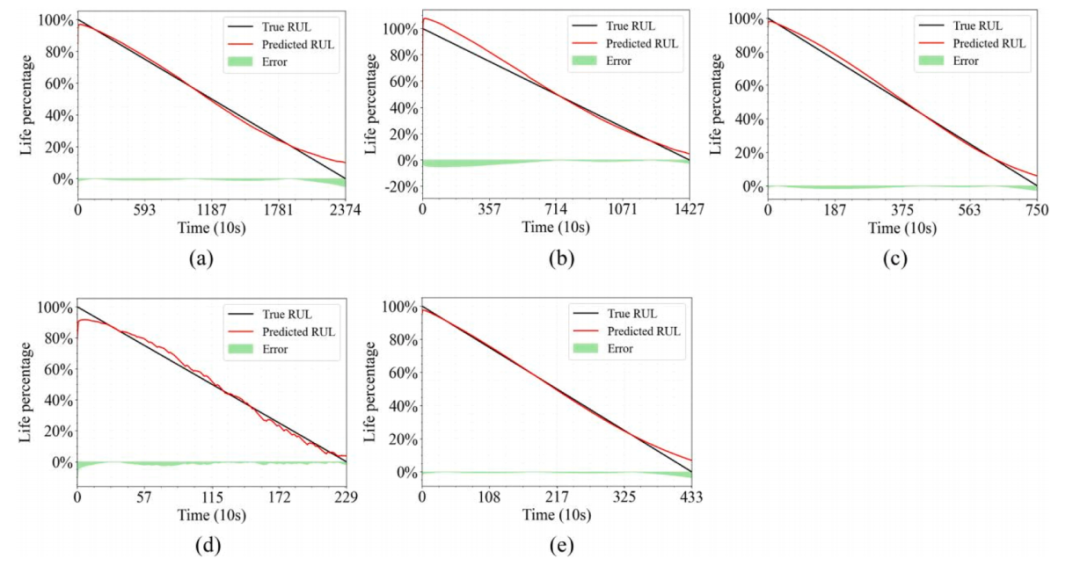
图6 预测结果;(a)数据集1-3,(b)数据集1-4,(c)数据集2-4,(d)数据集2-7,(e)数据集3-3
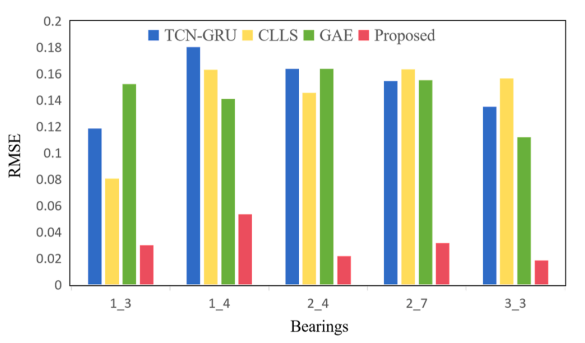
图7 预测误差的RMSE值
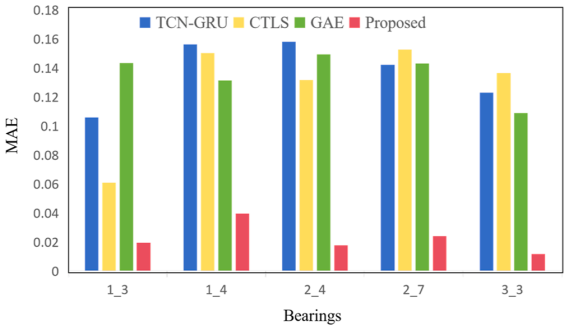
图8 预测误差的MAE值
4.2.3.案例研究二:XJTU-SY轴承数据集
为验证该技术的有效性,我们使用公开的XJTU-SY轴承数据集进行了进一步评估。为确保技术的适用性,我们设计了交叉验证实验,实验中使用的数据集详见表6。在不同运行条件下,每个实验选取一个数据集作为测试集,其余两个数据集作为训练集。具体来说,当使用数据集1-1作为测试集时,训练集采用数据集1-2和1-3;反之,当使用1-2作为测试集时,则采用1-1和1-3作为训练集。
表6 XJTU-SY数据集的实验设置

本研究将所提出方法的性能与TCNGRU、CTLS、GAE进行对比。采用Adam优化器,学习率设为0.001,训练过程持续200个周期。表7展示了该方法与替代方案的对比结果。数据显示,所提方法在保持较低RMSE和MAE的同时,显著提升了R²指标。以轴承1-2和轴承1-3为例,该方法分别实现了0.0452和0.0113的RMSE,以及0.9712和0.9985的R²,明显优于其他方法。这表明该模型在相对稳定的劣化过程中具有强大的拟合能力。在轴承2-1、轴承2-2等相对复杂的子数据集上,虽然整体误差略有上升,但所提出的方法仍以显著优势持续超越基准方法,展现出良好的鲁棒性和泛化能力。图9展示了部分实验组的预测曲线及误差数据。图11和图12分别呈现RMSE和MAE指标,对比了所提方法与其他模型在所有测试集上的表现。这些结果充分证明了该方法在预测能力上的优越性。
表7 提出方法和其他方法之间的性能比较
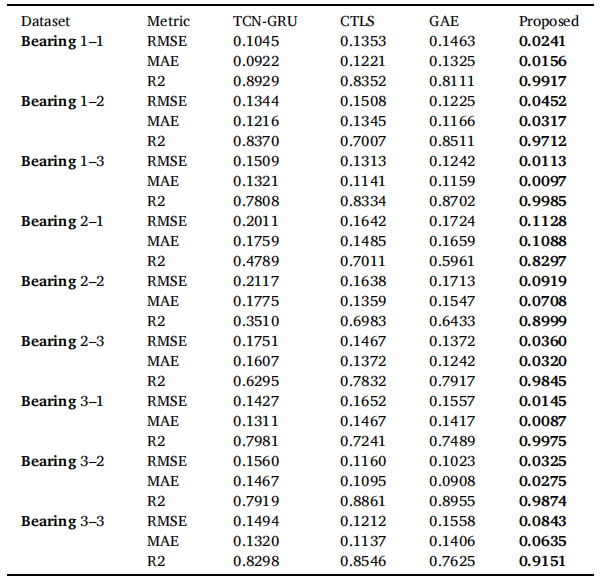
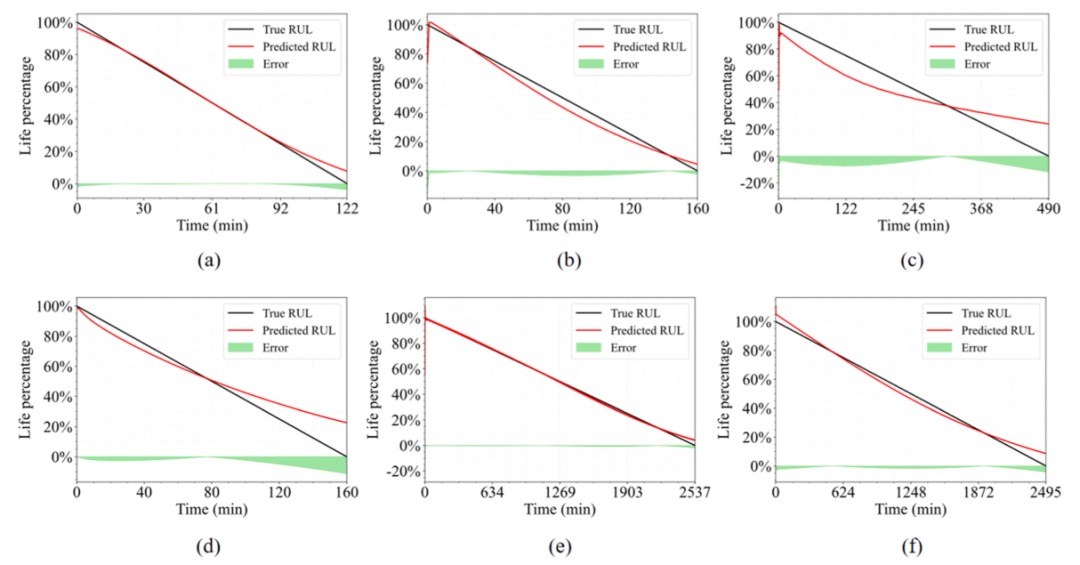
图9 预测结果; (a)数据集1-1、(b)数据集1-2、(c)数据集2-1、(d)数据集2-2、(e)数据集3-1、(f)数据集3-2
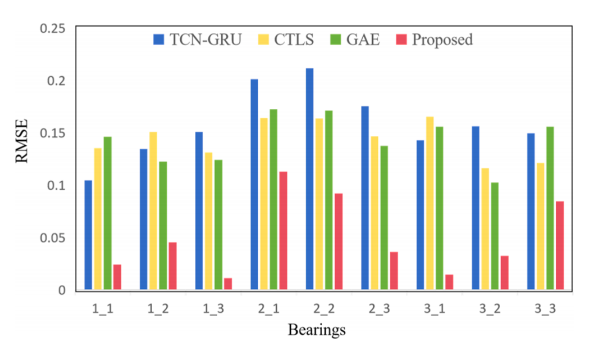
图10 预测误差的RMSE值
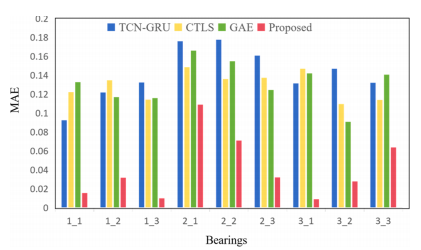
图11 预测误差的MAE值
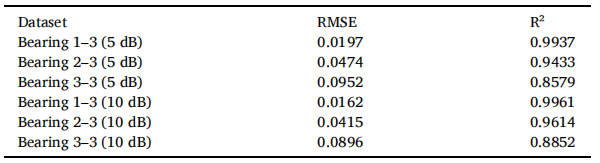
为评估系统在环境干扰下的鲁棒性,我们在XJTU-SY数据集上进行了噪声子集验证。该噪声子集通过在信噪比(SNR)为5 dB和10 dB的条件下添加高斯白噪声生成。表9展示了预测结果,结果显示与原始XJTU-SY相比,噪声子集下的RMSE值有适度提升,表明系统对噪声具有良好的泛化能力。
表9 添加噪声后的预测效果
4.2.4.复杂性与性能的权衡分析
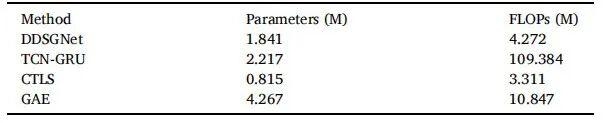
为评估DDSGNet的实际应用价值,我们从参数数量和浮点运算(FLOPs)两方面分析了其计算复杂度,并与基线方法(TCNGRU、CTLS和GAE)进行对比。表10汇总了模型复杂度数据。虽然DDSGNet的参数量略高于CTLS,但其预测准确率显著提升,同时保持更低的计算成本:4.272M FLOPs。与TCN-GRU相比,DDSGNet在计算量和内存占用方面均表现出色:运算量减少25倍以上,参数量缩减约17%,同时保持了更高的准确率。尽管GAE的计算量相当,但其参数数量是DDSGNet的两倍多,预测性能也明显较低。这些结果表明,DDSGNet在准确性和效率之间找到了最佳平衡点,非常适合在计算资源有限的工业环境中进行实时部署。
表10 模型复杂度
4.2.5.消融实验分析
为评估模型各组件对整体性能的贡献,我们开展了消融实验。通过系统性移除关键组件来探究其对模型性能的影响,具体细节见表8。为进一步分析各组件的作用,我们采用t-SNE对不同消融配置学习到的潜在特征嵌入进行可视化展示。如图12所示,完整的DDSGNet在整个退化过程中展现出平滑连续的嵌入轨迹,颜色从健康状态逐渐过渡到故障状态,这与RUL的缩短直接对应。当移除SplineCNN分支后,嵌入空间整体连贯性减弱,局部结构变得模糊不清,这表明其建模空间图拓扑信息的能力有所下降。 当消除DSAF约束时,模型结构变得松散,表明其捕捉复杂模式的能力下降。移除物理约束后,嵌入分布呈现无序状态,颜色分布也出现断裂。这些发现证实,每个组件对于学习稳健且物理一致的表征以预测RUL都至关重要。
表8 消融实验装置

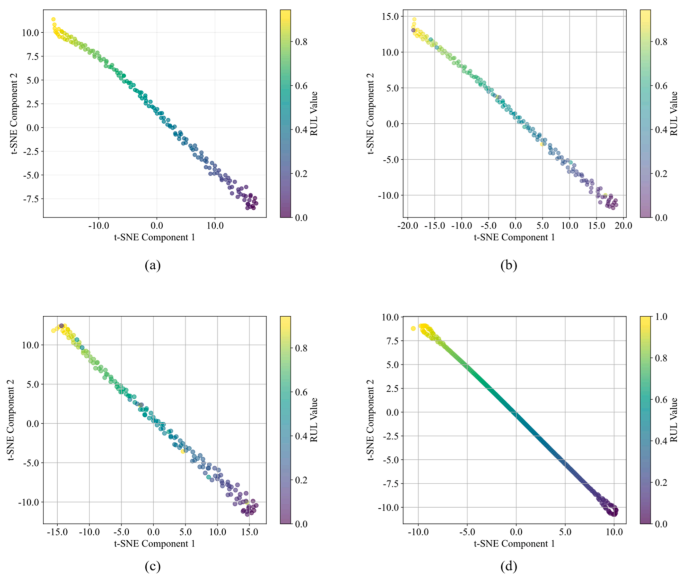
图12 (a)条件A、(b)条件B、(c)条件C和(d)条件D的特征可视化结果
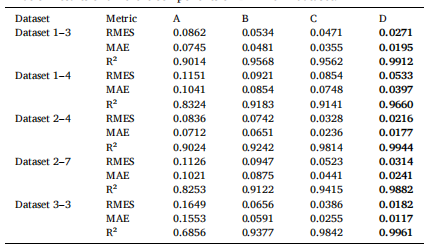
表11展示了PHM2012数据集上的消融实验结果。在条件A(移除SplineCNN)中,由于模型丧失了对连续局部特征演化的建模能力,导致RMSE显著上升(例如数据集1-3的RMSE升至0.0862),而R²则下降(例如降至0.9014),这削弱了其捕捉空间退化模式的能力。在条件B中,当用ReLU替代DSAF时,性能出现下滑,数据集1-3的RMSE值为0.0534。这种下降源于ReLU无法动态调整并提供平滑梯度,从而影响其在非线性特征拟合中的有效性。在条件C(移除物理约束)中,由于缺乏非负性和单调性约束,模型预测结果与轴承退化规律不符,导致物理一致性降低(例如数据集1-3的RMSE为0.0471)。完整模型(D)实现了最低的RMSE值(例如0.0271)和最高的R²值(例如数据集1-3的0.9912),充分展现了其各组件间的协同效应。
表11 PHM2012数据集不同组件的消融实验结果
DDSGNet的协同效应源于对全局、局部和时间特征的协同处理,专门用于轴承RUL预测。GCN(公式(1))通过处理输入振动信号提取全局拓扑特征,捕捉不同时间窗口内的整体劣化模式。SplineCNN(公式(5))通过建模连续的局部特征变化来补充这一过程,这对于检测细微的退化趋势至关重要。随后将这些全局与局部特征进行融合(公式(11)),构建出完整的空间表征。GRU模型通过处理该表征来整合时间动态变化,确保预测结果准确反映降解进程。该集成流程通过优化PhyMAE损失函数(公式(28))——该函数强制要求单调性和非负性——来实现这一目标,具体通过以下方式实现:
GCN技术的全局视角:捕捉不同时间窗口的广泛劣化模式,有效降低复杂工况建模误差。SplineCNN的局部精度:模拟平滑劣化趋势,减少GCN离散聚合固有的离散化误差。GRU的时序一致性:使预测结果与退化过程的时序演变保持一致,提升物理一致性。
这种协同方法确保了DDSGNet能够捕捉多尺度时空模式,这是单一模块或成对模块都无法实现的。SplineCNN中的B样条核因其Lipschitz连续性提供了稳定的梯度流,而GRU的门控机制则缓解了梯度消失问题,从而实现了损失函数的稳健优化。消融实验验证了这种协同效应,表明与部分配置相比,完整模型在RMSE指标上显著降低,同时在R²指标上表现更优。
4.2.6.超参数敏感性分析
为验证图构建过程中超参数的选择,我们对KNN参数、时间窗口大小、学习率和批量大小进行了敏感性分析,评估了这些参数对DDSGNet在XJTU-SY数据集(bearing13)(表12)上的性能影响。
表12 XJTU-SY数据集上不同组件的消融实验结果
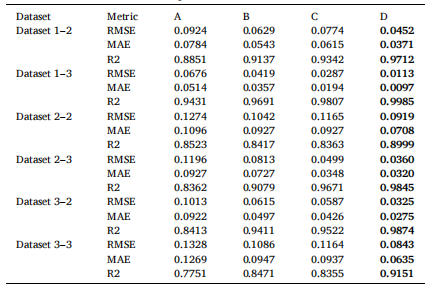
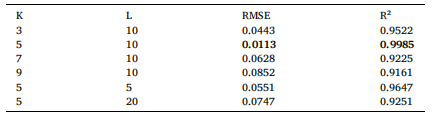
表13展示了K取值为{3,5,7,9}时,滑动窗口长度L分别为5、10和20个时间步长的实验结果。当K=5时,DDSGNet模型取得了RMSE=0.0175和R²=0.9964的优异表现,显著优于K=3(RMSE=0.0443,R²=0.9522)因邻域连接性不足的情况,以及K=9(RMSE=0.0852,R²=0.9161)因引入远邻噪声的影响。采用10个时间步长的时序窗口能实现最佳性能,这种设置在时间分辨率与特征稳定性之间找到了平衡点。相较于仅捕捉信号变化不足的5步长窗口,以及过度平滑关键退化趋势的20步长窗口,该时序窗口方案展现出更优的性能表现。这些结果证实,K=5和L=10是建模轴承退化模式的理想参数。在测试训练相关参数时,我们评估了学习率({0.0005,0.001,0.005})和批量大小({16,32,64})的影响。0.001的学习率找到了最佳平衡点,不仅使RMSE值最低,还实现了最高的R²值;而0.0005会导致收敛速度变慢,0.005则会使训练过程不稳定。32的批量大小被认定为最优选择,相比16的批量大小会引入更多噪声,而64的批量大小则会降低更新频率。最终我们选择了最优配置(K=5,L=10,学习率=0.001,批量大小=32),该配置在验证集上观测到的RMSE值最低。
表13 KNN参数(K)和时间窗口大小对XJTUSY的敏感性分析
4.2.7.模型方差分析
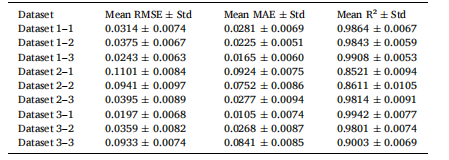
为评估DDSGNet的稳定性,我们在XJTU-SY数据集上使用五个不同随机种子(42、123、456、789、1000)进行了实验。表14展示了各运行中RMSE、MAE和R²的均值与标准差。这些结果表明,DDSGNet在不同初始化条件下对轴承RUL预测的可靠性。
表14 XJTU-SY上多次运行的模型方差
4.2.8.收敛性分析
为评估DSAF的收敛特性,我们在XJTU-SY数据集(数据集1-3)上将其训练性能与ReLU、Swish和Sigmoid进行对比。图13展示了训练损失曲线,结果显示DSAF不仅收敛速度更快,最终损失值也更低。DSAF的优异收敛性主要得益于其注意力机制——该机制能自适应地对退化相关特征进行加权,并通过平滑的Swish驱动梯度实现优化。
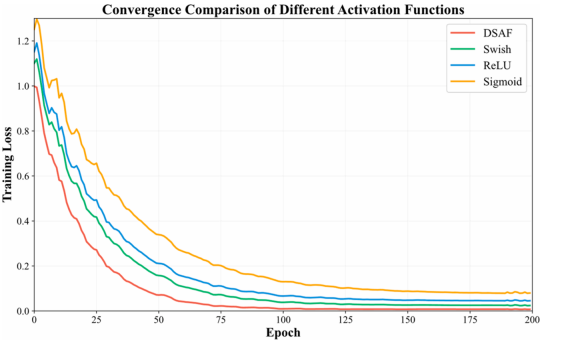
图13 不同激活函数的训练损失曲线
4.2.9.样条核参数与边缘属性的敏感性分析
我们使用XJTU-SY数据集1-3对SplineCNN的核参数和边属性进行了敏感性分析。具体而言,针对核参数,我们考察了核尺寸的影响,将其设置为{3,5,7}三种不同值,同时保持其他参数不变。对于边属性,我们评估了不同距离度量方法的敏感性,比较了欧氏距离和余弦距离。分析结果详见表15,其中包含RMSE值和决定系数R²。
表15 XJTU-SY模型中核尺寸与边缘属性的敏感性分析
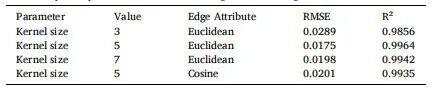
实验数据表明,5的最优卷积核尺寸能同时实现最低RMSE值和最高R²值,这表明其感受野平衡性良好,能有效捕捉局部退化特征。当卷积核尺寸缩小至3时,模型会出现欠拟合现象,RMSE值达到0.0289;而当卷积核尺寸增大至7时,由于过度平滑导致冗余问题,RMSE值会略微上升至0.0198。
采用欧氏距离作为边缘属性时,其性能优于余弦距离。欧氏距离能准确反映振动信号的幅度差异,这与材料劣化程度的强度相对应;而余弦距离侧重于方向性,由于忽略绝对变化,会导致精度略有下降。
5 结论
本文提出了一种双通道框架DDSGNet,用于精准预测轴承剩余使用寿命(RUL)。该模型通过整合全局拓扑建模的GCN、连续局部特征演化的SplineCNN以及时序依赖分析的GRU,有效捕捉轴承振动信号中的时空退化特征。采用基于注意力机制的自适应加权和Swish驱动平滑梯度的DSAF,显著提升了非线性特征拟合精度和训练稳定性。同时,通过PhyMAE约束确保预测结果的非负性和单调性,保证物理一致性。在IEEE PHM和XJTU-SY数据集上的实验表明,DDSGNet模型在准确性和鲁棒性方面均优于现有最优方法。该模型在预测性维护领域展现出巨大应用潜力,未来研究将重点探索跨域适配与实时RUL预测技术,以进一步提升其适用性。





