首页 发现 课程 培训 文章 案例 问答 需求 服务 行家 赛事
消息
首页/文章/ 详情

预处理共轭梯度法（PCG）与三维有限元分析C++编程实现

外太空土豆儿
外太空土豆儿
3小时前浏览7

摘要：

  根据有限元方程和稀疏矩阵的特性，在综合考虑最速下降法（SD）、共轭梯度法（CG）和预处理共轭梯度法（PCG）的优势和局限之后，选择了第三种迭代算法plus——基于PCG的逐个单元法（EBE），对角线预处理（Jacobi）。网格划分和单元刚度的生成，延用直接算法的方案，加载和约束边界条件亦复如是，但是无需组装整体刚度矩阵。
  采用C++语言实现迭代算法设计，并给出完整源码。求解有限元方程，得到各单元节点的位移向量，回代得到各单元积分点的应力。使用该程序分别对弹性立方实体（均布荷载）和悬臂钢梁（集中荷载）进行静力分析，计算结果与直接算法对比，精准度满足要求。还讨论了迭代法的优势与局限性，与直接法做对比。

关键词：

  逐个单元法（EBE），预处理共轭梯度法（PCG），预条件子，对角线预处理（Jacobi），共轭梯度法（CG），最速下降法（SD），迭代法，有限单元法（FEM），C++编程。

1. 引言

  对于线弹性固体力学的静力平衡问题，经典的有限元计算机程序是基于单元组装技术的。所有单元的刚度矩阵km和荷载向量f分别组装成总刚度矩阵K和总荷载列阵F，得到静力平衡问题的基本方程：

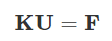
然后通过高斯消元法或各种plus版本，求解线性方程得到总位移向量U，回代得到各单元网格节点的位移和内力等物理量。

  那么问题来了：内存溢出怎么办？ 随着问题规模的扩大，总刚度矩阵K需要相当大的存储空间。既然直接算法求解线性方程组遇到瓶颈，那就用迭代算法，试试就试试。

  本文的网格划分和单元刚度的生成，延用《六面体单元与弹性实体的三维有限元分析C++编程实现》的方案，但是无需组装整体刚度矩阵。对程序算法进行改进，具体做法如下：

  • 新增storkm，以保留各个单元刚度矩阵，无整体刚度组装；
  • 新增迭代相关：计数器cg_iters、次数上限cg_limit、收敛误差cg_tol；
  • 新增PCG相关：对角前置向量diag_precon，参数alpha、beta，向量内积up、kp以及一系列向量；
  • 基于PCG的逐个单元法（EBE）替代原来的直接算法（Cholesky分解）；
  • 可视化处理：将三维有限元方程求解前后的数据文件生成EnSight Gold格式。

2. 预处理共轭梯度法（PCG）

2.1 问题描述与等价性

  静力平衡问题的有限元基本方程KU=F，可以根据最小势能原理推导得到。系统总势能Π可以表示为应变能和外力势能之和，即：

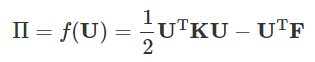
其中系统总刚度矩阵K为实对称正定矩阵，系统总势能Π可以表示为U的函数，静力平衡状态对应着函数f(U)最小值。

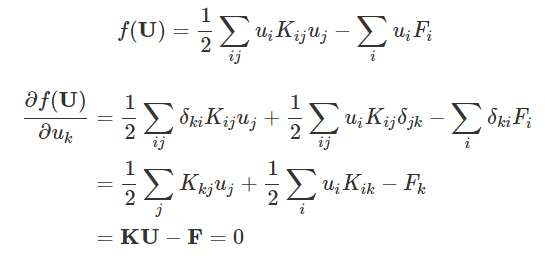
也就是说，求出f值最小的解U*等价于求解线性方程组KU*=F，而函数f(U)梯度表达式：

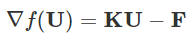
令函数f(U)梯度为零，存在等价线性系统，如下所示：

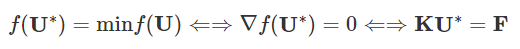
函数f(U)可以看做是一个超级碗（开口朝天），碗底最低点就是硅基生物的寻宝目的地。

2.2 为何不用最速下降法（SD）？

想象自己在群山环绕中，如何到达山底？步骤如下：

  1. 确定初始位置，找到最陡下降方向；
  2. 沿着选定方向一直走到底（不再下降），停下来；
  3. 环视一周，找到新的最陡下降方向（拐弯），一直走到底（不再下降），停下来；
  4. 重复步骤3，直至到达群山之底。

以上就是最速下降法（Steepest Descent Method，SD）的通俗描述。核心思想是：找到函数在当前位置的梯度，并沿着梯度的反方向移动，迭代收敛到终点位置。翻译成数学语言如下：

最速下降法（SD）求解KU=F的标准流程：

  1. 选取初始位置U0，给定终止误差ε＞0，令k:=0；

  2. 计算函数f(U)在当前位置的梯度：

         

如果梯度的范数小于预设的阈值ε，则停止迭代，输出当前位置Uk；

否则进行第3~5步；

  1. 找到梯度的反方向Rk，作为最速下降方向：

         

  2. 选择合适的步长αk，使得函数f(U)在当前方向取得最小值：

         
  1. 更新位置和方向：
         
  1. 重复第2~5步，直到满足终止条件，或者达到最大迭代次数。

看上去似乎很美好：最速下降法（SD）每一步朝当前梯度（最陡的下坡方向）走一小步。
然而，现实很骨感：高维问题中易产生锯齿现象（Zig-zag Path），收敛速度慢，尤其当目标函数的等值线为扁长椭球时。通俗描述为，如果函数的“超级碗”被拉扁了（沿某个方向特别陡，另一个方向特别缓），那么最速下降就会在两条方向之间来回“之”字形游走，不知猴年马月到碗底。

最速下降法（SD）的缺点：当矩阵K的特征值分布跨度很大时，条件数cond(K)增大，最速下降会在各个主轴方向来回“锯齿”逼近，收敛很慢。

  有限元方程中的刚度矩阵K为对称正定稀疏矩阵，零元素较多，但非零元分布（如：对角占优程度）直接影响条件数。稀疏矩阵条件数往往过高，由于其收敛性缺陷、计算效率不足以及对稀疏性利用不充分等问题，稀疏矩阵求解线性方程组时较少采用最速下降法。

2.3 共轭梯度法（CG）

  简言之，共轭梯度法（Conjugate Gradient Method, CG）就是在一个“扁碗”上找最低点的聪明方法：它每一步不仅沿着梯度走，还保证新方向和旧方向互不“打架”，因此不会来回折返，收敛更快，特别适合大规模、稀疏的线性问题。核心思想：每次的下坡方向，既能去掉当前的“高架”，又不会破坏前面已经“清理干净”的方向。

共轭梯度法(CG)求解KU=F的标准流程：

  1. 初始化：选取初始位置U0，给定终止误差ε＞0，令k:=0；
    计算初始残差：       R0 = F - KU0

    设置初始搜索方向：P0 = R0

  2. 计算步长αk ，使得函数f(U)在当前方向Pk取得最小值：

  3. 更新→解向量和残差

  4. 计算共轭方向系数βk：

  1. 生成新的搜索方向Pk+1：

  6. 终止条件：

  当残差范数小于预设阈值ε或达到最大迭代次数时，停止迭代，输出近似解Uk；

  否则重复第2~5步，直到满足终止条件。

可以看出，共轭梯度法（CG）与最速下降法（SD）的不同：CG引入了共轭方向系数βk 在“超级椭圆碗”速降时，每次转弯不是SD直接采用最陡方向，而是瞻前顾后，确保新旧方向不打架，以构造出共轭新方向。

2.4 预处理共轭梯度法（PCG）

  是否可以进一步改善线性方程组的数值特性，从而加速迭代算法的收敛？
预处理共轭梯度法（Preconditioned Conjugate Gradient, PCG）是一种用于高效求解大型稀疏对称正定线性方程组的迭代算法，通过引入预条件子改善系数矩阵的条件数，显著提升收敛速度。其核心机制是降低条件数和集中 特征值分布。用数学语言表述为：

  对于线性方程组KU=F，当原始系数矩阵K的条件数cond(K)过大时，共轭梯度法（CG）收敛缓慢，此时构造预条件子M，将方程组转化为：

新系数矩阵的条件数大幅减小，使得迭代步数大幅减少：

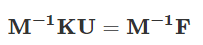
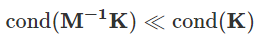
最理想的情况是条件数接近1，收敛速度接近直接解法：

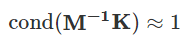
预处理共轭梯度法（PCG）求解KU=F的标准流程：

  1. 初始化：选取初始位置U0，给定终止误差ε＞0，令 k:=0；
    初始残差：      R0 = F - KU0

    预处理残差：   Z0 =M-1R0

    初始搜索方向：P0 = Z0

  2. 计算步长αk，使得函数f(U)在当前方向Pk取得最小值：

  3. 更新→解向量和残差

  4. 计算共轭方向系数βk：

  5. 生成新的搜索方向Pk+1：

  1. 终止条件

    当残差范数小于预设阈值ε或达到最大迭代次数时，停止迭代，输出近似解Uk；
    否则重复第2~5步，直到满足终止条件。      
可以看出，预处理共轭梯度法（PCG）与共轭梯度法（CG）的不同：PCG引入预条件子M对应的预处理残差Zk，于是计算步长αk、共轭方向系数 βk、搜索方向Pk的表达式有所不同。

  预条件子M需满足两大条件：高效可求逆和近似原系数逆阵。
  当线性系统的系数矩阵，满足“对称正定稀疏矩阵、可获得良好预条件”的前提下，预处理共轭梯度法（PCG）往往是首选。

常见的预条件子类型、构造方式及效果如下：

预条件子类型构造方式收敛提升效果
对角线预处理    
（Jacobi）    
M = diag(K)
简单高效，内存占用低，忽略非对角元素    
不完全Cholesky分解    
（IC）    
M = LLT
显著改善条件数，但分解计算成本较高    
对称逐次超松弛    
（SSOR）    
M = (D+ωL)D-1(D+ωL)T
易于并行，依赖参数ω    

  不只是Jacobi、IC、SSOR这些分解式预条件有助于压缩系数矩阵的谱分布，还可以采取更进一步的优化措施：

  • 重启策略：对于长迭代或数值误差积累，可每隔一定步数重新设置残差与搜索方向，以清除漂移。

  • 并行化与稀疏存储：利用SciPy的并行BLAS或GPU加速矩阵-向量乘，提高运算吞吐。

  • 多重网格：将CG嵌入多重网格框架（MGCG），在不同尺度上加速收敛。


3. 逐个单元法（EBE）

从共轭梯度法（CG）的标准流程可以看出：

  CG算法仅涉及到一些简单的向量操作，例如，向量内积、向量加减、向量与标量的乘除；唯一涉及到矩阵的，是刚度矩阵K与搜索方向向量P的点乘。由于P是已知向量，KP可以按单元一个接一个地执行（逐个单元法），根本就不需要组装总刚度矩阵K，完美避开了高斯消元法等直接法的庞大开销。也就是说：

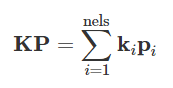
其中，nels是单元数，ki是第i个单元的单元刚度矩阵，pi是P相应于第i个单元的部分。

从预处理共轭梯度法（PCG）的标准流程可以看出:

  PCG算法（相对于CG）采取优化措施以加速收敛，也就是预条件子M改善原有的系数矩阵K，使得新构造出的系数矩阵M-1K的条件数减少，条件数接近1为最佳喔。预条件子M应该是易于求逆的，否则就没什么用；或者是易于求解预处理线性方程组，如下：

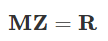
通过求解以上方程组，得到预处理残差Z，由此看出：

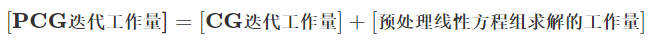
如果能够显著加快收敛的速度，那么额外付出的预处理工作量是值得的。这就看预条件子M的表现。常见的3种预条件子M——对角线预处理（Jacobi）、不完全Cholesky分解（IC）、对称逐次超松弛（SSOR），具体表现如下：

  • Jacobi预处理：内存占用低，并行扩展性强。至于收敛速度，对于系数矩阵对角占优的问题是极好的；但是对于其他实对称正定矩阵，表现得中规中矩，比没有强。
  • IC预处理：内存占用大大降低，并行扩展性还不错，这两点表现不如Jacobi预处理。但是收敛速度大大加快，尤其是系数矩阵为非对角占优的情况，表现极为强势，碾压Jacobi预处理。
  • SSOR预处理：文献[2]将其ω=1的特例，也就是高斯-赛德尔（Gauss-Seidel）预条件子，与雅可比（Jacobi）预条件子做对比，两种方法都能有效加快收敛速度，Gauss-Seidel更胜一筹。实际上SSOR预处理的表现，依赖参数ω。内存占用和并行扩展方面，不如Jacobi预处理。

基于PCG的逐个单元法（EBE）：

  逐个单元法，顾名思义Element-by-Element Method（简称EBE）。
核心思想：避免总刚度矩阵的组装。在迭代过程中直接利用单元刚度矩阵km计算局部贡献，通过向量累加更新全局解，避免存储大型稀疏矩阵。至于预处理的方式：

  • Jacobi预条件子是最简单的；
  • 利用单元矩阵的不完备Cholesky分解，构造总刚度阵的近似，形成预条件矩阵；
  • 文献[2]注意到SSOR预条件子也可以定义为下三角矩阵和上三角矩阵的乘积，通过两次回代可以求解预处理线性方程组，得到预处理残差。这和IC预处理有相似之处。

本文将采取Jacobi预条件子：

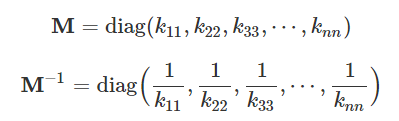
可以看出，M是K的对角线矩阵，M的逆阵是对角线元素的倒数。无需组装总刚度矩阵，就能轻松获取。接下来就是见证奇迹的时刻。


4. 程序设计C++

4.1 网格生成与后处理

对于简单规则的几何体：自定义函数/子程序生成三维网格

  对于复杂的几何体，更普遍的做法：借助前处理软件/工具生成网格，然后直接读入各节点坐标、各单元节点编号、荷载和边界条件等信息。

后处理步骤：自定义函数/子程序生成EnSight Gold文件

  • 通过mesh_ensi()和dis msh_ensi()提取数据，生成一系列EnSight Gold文件；
  • 利用可视化工具ParaView查看EnSight Gold文件，进行FEM后处理。

4.2. 主程序流程图及C++源码

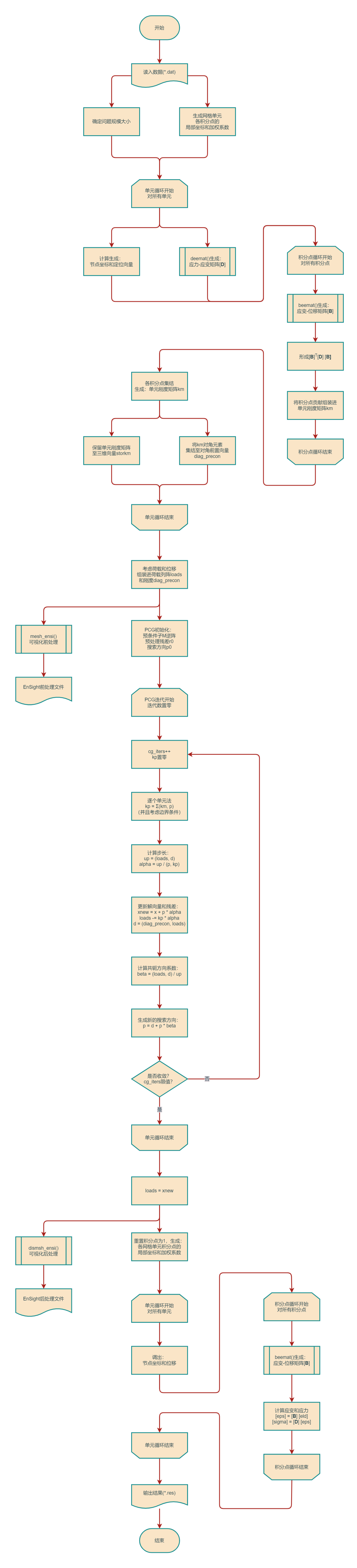
图1：主程序流程图









































































































































































































































































































































































//===================================================================//Program No.13  Diagonally preconditioned conjugate gradient solver.//        3D strain of an elastic solid using brick hexahedra.//              No global stiffness matrix assembly.//===================================================================#include "geom.h"#include "main.h"#include <fstream>#include <iostream>#include <string>#include <utility>#include <vector>#include <iomanip>using namespace std;
int main() {  int cg_iters;//PCG迭代计数器  int cg_limit;//PCG迭代上限  int fixed_freedoms;//固定位移数  int loaded_nodes;//受载节点数  int ndim = 3;//维数  int ndof;//单元自由度  int nels;//单元数  int neq;//网格自由度  int nip;//单元积分节点数  int nn;//节点数  int nod;//单元节点数  int nodof = 3;//节点自由度  int nprops = 2;//材料特性数  int np_types;//材料类型数  int nr;//约束节点数  int nst = 6;//应力（应变）项数目  int nxe, nye, nze;//x、y、z向单元数  double alpha, beta;//PCG参数  double cg_tol;//PCG收敛误差  double det;//雅可比矩阵行列式  double penalty = 1.0e20;           //罚因子     double up;//PCG向量内积  string element = "hexahedron";//单元类型 = 六面体  string fin_name, fout_name;//读入文件名，写出文件名  pair<string, string> argv;//文件名返回值  bool cg_converged = false;//PCG是否收敛
//========================= input and initialisation =========================  argv = getname();  fin_name = argv.first;  ifstream fin(fin_name, ios::in);  fout_name = argv.second;  ofstream fout(fout_name, ios::out);
  fin >> nod >> nxe >> nye >> nze >> nip;//从文件读入：单元节点数，x/y/z向单元数，单元积分节点数  fin >> cg_tol >> cg_limit >> np_types;//从文件读入：PCG收敛误差与迭代上限，材料类型数  auto result0 = mesh_size(element, nod, nxe, nye, nze);//生成：单元数，节点数  nels = result0.first;  nn = result0.second;  ndof = nod * nodof;//单元自由度  vector<double> eld(ndof);//单元节点位移（单元自由度）  vector<double> eps(nst);//应变项（应力/应变项数目）  vector<int> etype(nels, 1);//单元特性类型向量（单元数）  vector<double> fun(nod);//形函数（单元节点数）  vector<int> g(ndof);//单元定位向量（单元自由度）  vector<double> gc(ndim);//积分点坐标（维数）  vector<int> num(nod);//单元节点编号向量（单元节点数）  vector<double> sigma(nst);//应力项（应力/应变项数）  vector<double> weights(nip);//数值积分加权系数（单元积分节点数）  vector<double> x_coords(nxe + 1);//网格排列的x方向坐标（单元行数 + 1）  vector<double> y_coords(nye + 1);//网格排列的y方向坐标（单元行数 + 1）  vector<double> z_coords(nze + 1);//网格排列的z方向坐标（单元行数 + 1）  vector<vector<double> > bee(nst, vector<double>(ndof));//应变-位移矩阵（应力/应变项数, 单元自由度）  vector<vector<double> > coord(nod, vector<double>(ndim));//单元节点坐标（单元节点数, 维数）  vector<vector<double> > dee(nst, vector<double>(nst));//应力-应变矩阵（应力/应变项数, 应力/应变项数）  vector<vector<double> > der(nod, vector<double>(ndim));//局部坐标下形函数的偏导数（单元节点数, 维数）  vector<vector<double> > deriv(nod, vector<double>(ndim));//整体坐标下形函数的偏导数（单元节点数, 维数）  vector<vector<double> > g_coord(nn, vector<double>(ndim));//所有单元的节点坐标（节点数, 维数）  vector<vector<int> > g_g(nels, vector<int>(ndof));//总单元定位矩阵（单元数，单元自由度）  vector<vector<int> > g_num(nels, vector<int>(nod));//总单元节点编号矩阵（单元数, 单元节点数）  vector<vector<double> > jac(ndim, vector<double>(ndim));//雅可比矩阵（维数, 维数）  vector<vector<double> > km(ndof, vector<double>(ndof));//单元刚度矩阵（单元自由度, 单元自由度）  vector<vector<int> > nf(nn, vector<int>(nodof, 1));//节点自由度矩阵（节点数，节点自由度）  vector<vector<double> > points(nip, vector<double>(ndim));//单元积分点坐标（单元的积分点数, 维数）  vector<vector<double> > prop(np_types, vector<double>(nprops));//单元特征矩阵（材料类型数, 材料特性数）  vector<vector<vector<double> > > storkm(nels, vector<vector<double> >(ndof, vector<double>(ndof)));  //保留单元刚度矩阵（单元数, 单元自由度, 单元自由度）
  for (int i = 0; i < np_types; i++) {//从文件中读入:单元特征矩阵    for (int j = 0; j < nprops; j++)      fin >> prop[i][j];  }  if (np_types > 1) {//从文件中读入:单元特性类型向量    for (int i = 0; i < nels; i++)      fin >> etype[i];  }  for (int i = 0; i <= nxe; i++)//从文件中读入:网格排列的x方向坐标    fin >> x_coords[i];  for (int i = 0; i <= nye; i++)        //从文件中读入:网格排列的y方向坐标    fin >> y_coords[i];  for (int i = 0; i <= nze; i++)//从文件中读入:网格排列的z方向坐标    fin >> z_coords[i];  fin >> nr;//从文件中读入:约束节点数  vector<int> k1(nr);//约束节点编号向量（约束节点数）  if (nr > 0) {    for (int i = 0; i < nr; i++) {//从文件中读入:约束节点编号及自由度      fin >> k1[i];      for (int j = 0; j < nodof; j++) {        int m = k1[i] - 1;        fin >> nf[m][j];      }    }  }  auto result1 = formnf(nf);  neq = result1.first;//返回：网格自由度数目  nf = result1.second;//生成：节点自由度矩阵  fout << " There are " << neq << " equations." << endl;  cout << " There are " << neq << " equations." << endl;  vector<double> d(neq);//前置rhs向量（网格自由度）  vector<double> diag_precon(neq, 1.0);//对角前置向量（网格自由度）  vector<double> loads(neq);//总体荷载/位移向量（网格自由度）  vector<double> r(neq);//PCG“残差”向量（网格自由度）  vector<double> p(neq);//PCG“下降”向量（网格自由度）  vector<double> kp(neq);//PCG“迭代值”向量（网格自由度）  vector<double> x(neq), xnew(neq);//PCG“老”和“新”求解向量（网格自由度）  auto result2 = sample(element, nip, ndim);  points = result2.first;        //生成：单元积分点坐标  weights = result2.second;  //生成：加权系数
//======== element stiffness integration, storage and preconditioner =========  for (int i = 0; i < nels; i++) {    int m = etype[i] - 1;    dee = deemat(prop[m][0], prop[m][1], nst);//生成：应力-应变矩阵[D]    auto result3 = hexahedron_xz(i, nod, x_coords, y_coords, z_coords);    coord = result3.first;//生成：单元节点坐标矩阵    num = result3.second;//生成：单元节点编号向量    g = num_to_g(num, nf);//生成：单元定位向量    g_num[i] = num;//第i个单元的节点编号向量    for (int j = 0; j < nod; j++) {      int k = num[j] - 1;      g_coord[k] = coord[j];        //第i个单元的节点坐标矩阵    }    g_g[i] = g;//第i个单元的定位向量
    fill(km.begin(), km.end(), vector<double>(ndof, 0.0));    vector<vector<double> > btdb(ndof, vector<double>(ndof, 0.0));    for (int ii = 0; ii < nip; ii++) {      der = shape_der(ii, nod, points);//生成：局部坐标下形函数的偏导数      jac = matmul(transpose(der), coord);       //生成：雅可比矩阵      det = determinant(jac);//生成：雅可比矩阵行列式      jac = invert(jac);//生成：雅可比矩阵的逆      deriv = matmul(der, jac);//生成：整体坐标下形函数的偏导数      bee = beemat(nst, ndof, deriv);//生成：应变-位移矩阵[B]      btdb = matmul(matmul(transpose(bee), dee), bee);      for (int jj = 0; jj < ndof; jj++) {        for (int kk = 0; kk < ndof; kk++)          btdb[jj][kk] *= det * weights[ii];      }      for (int jj = 0; jj < ndof; jj++) {        for (int kk = 0; kk < ndof; kk++)          km[jj][kk] += btdb[jj][kk];      }//生成：单元刚度矩阵    }    storkm[i] = km;//第i个单元的刚度矩阵    for (int k = 0; k < ndof; k++) {      if (g[k]) {        int m = g[k] - 1;        diag_precon[m] += km[k][k];//生成：对角前置向量      }    }  }
//============= invert the preconditioner and get starting loads =============  fin >> loaded_nodes;//从文件读入：受载节点数  vector<int> k2(loaded_nodes);//初始化：受载节点编号向量  if (loaded_nodes) {//从文件读入：受载节点编号，相应荷载向量    for (int i = 0; i < loaded_nodes; i++) {      fin >> k2[i];      int m1 = k2[i] - 1;      for (int j = 0; j < nodof; j++) {        if (nf[m1][j]) {          int m2 = nf[m1][j] - 1;          fin >> loads[m2];        }        else          fin.ignore(5);      }    }  }  fin >> fixed_freedoms;//从文件读入：固定位移的数量  vector<int> node(fixed_freedoms);//固定节点向量  vector<int> no(fixed_freedoms);//固定自由度编号向量  vector<int> sense(fixed_freedoms);//固定自由度的检测向量  vector<double> value(fixed_freedoms);//固定位移向量  vector<double> store(fixed_freedoms);//储存增广对角项  if (fixed_freedoms) {    for (int i = 0; i < fixed_freedoms; i++) {      fin >> node[i] >> sense[i] >> value[i];      int j = node[i] - 1;      int k = sense[i] - 1;      no[i] = nf[j][k];      int m = no[i] - 1;      diag_precon[m] += penalty;      loads[m] = diag_precon[m] * value[i];      store[i] = diag_precon[m];    }  }
  //生成：前处理Ensight Gold格式文件，该格式文件可以使用ParaView查看  mesh_ensi(fin_name, g_coord, g_num, element, etype, nf, loads, 1, 1, 0.0, true);
  //PCG初始化：预条件子M逆阵, 预处理残差r0, 搜索方向p0  for (int i = 0; i < neq; i++) {    diag_precon[i] = 1.0 / diag_precon[i];    d[i] = diag_precon[i] * loads[i];    p[i] = d[i];  }
//========================== PCG equation solutions ==========================  cg_iters = 0;  fill(x.begin(), x.end(), 0.0);
  while (!cg_converged && cg_iters != cg_limit) {    cg_iters++;    fill(kp.begin(), kp.end(), 0.0);
    //逐个单元法 kp = Σki·pi    for (int i = 0; i < nels; i++) {      g = g_g[i];      km = storkm[i];      for (int j = 0; j < ndof; j++) {        if (g[j]) {          int m1 = g[j] - 1;          for (int k = 0; k < ndof; k++) {            if (g[k]) {              int m2 = g[k] - 1;              kp[m1] += km[j][k] * p[m2];            }          }        }      }    }    if (fixed_freedoms) {      for (int i = 0; i < fixed_freedoms; i++) {        int m = no[i] - 1;        kp[m] = p[m] * store[i];      }    }
    //PCG迭代流程    up = matmul(loads, d);    alpha = up / matmul(p, kp);    for (int i = 0; i < neq; i++) {      xnew[i] = x[i] + p[i] * alpha;      loads[i] -= kp[i] * alpha;      d[i] = diag_precon[i] * loads[i];    }    beta = matmul(loads, d) / up;    for (int i = 0; i < neq; i++) {      p[i] = d[i] + p[i] * beta;    }
    //PCG是否终止？    auto result4 = checon(xnew, x, cg_tol);    cg_converged = result4.first;    x = result4.second;  }  fout << " Number of cg iterations to convergence was " << cg_iters << endl;  cout << " Number of cg iterations to convergence was " << cg_iters << endl;  fout << endl << "  Node   x-disp      y-disp      z-disp" << endl;  cout << endl << "  Node   x-disp      y-disp      z-disp" << endl;
  loads = xnew;  for (int i = 0; i < nn; i++) {  fout << setw(4) << i + 1;  cout << setw(4) << i + 1;    for (int j = 0; j < nodof; j++) {      if (nf[i][j]) {        int k = nf[i][j] - 1;        fout << setw(14) << scientific << setprecision(4) << loads[k];        cout << setw(14) << scientific << setprecision(4) << loads[k];      }      else {        fout << "    0.0000e+00";        cout << "    0.0000e+00";      }    }    fout << endl;    cout << endl;  }
  //生成：后处理Ensight Gold格式文件，该格式文件可以使用ParaView查看  dis msh_ensi(fin_name, 1, nf, xnew);
//================ recover stresses at nip integrating points ================  nip = 1;  points.resize(nip, vector<double>(ndim));  weights.resize(nip);  auto result4 = sample(element, nip, ndim);  points = result4.first;//生成：单元积分点坐标  weights = result4.second;//生成：加权系数
  fout << endl << " The integration point (nip=" << nip << ") stresses are:" << endl;  cout << endl << " The integration point (nip=" << nip << ") stresses are:" << endl;  fout << " Element  x-coord       sig_x         tau_xy" << endl;  cout << " Element  x-coord       sig_x         tau_xy" << endl;  fout << "          y-coord       sig_y         tau_yz" << endl;  cout << "          y-coord       sig_y         tau_yz" << endl;  fout << "          z-coord       sig_z         tau_zx" << endl;  cout << "          z-coord       sig_z         tau_zx" << endl;
  for (int i = 0; i < nels; i++) {    fout << setw(4) << i + 1;    cout << setw(4) << i + 1;    if (np_types > 1) {      int m = etype[i] - 1;      dee = deemat(prop[m][0], prop[m][1], nst);    }//生成：应力-应变矩阵[D]    else      dee = deemat(prop[0][0], prop[0][1], nst);    num = g_num[i];//生成：第i个单元的节点编号向量    for (int j = 0; j < nod; j++) {      int k = num[j] - 1;      coord[j] = g_coord[k];      //生成：第i个单元的节点坐标矩阵    }    g = g_g[i];//生成：第i个单元的定位向量    for (int k = 0; k < ndof; k++) {      if (g[k]) {        int m = g[k] - 1;        eld[k] = loads[m];//生成：第i个单元的位移向量      }      else        eld[k] = 0.0;    }    for (int ii = 0; ii < nip; ii++) {      fun = shape_fun(ii, nod, points);//生成：形函数      der = shape_der(ii, nod, points);//生成：局部坐标下形函数的偏导数      gc = matmul(fun, coord);//生成：积分点坐标      jac = matmul(transpose(der), coord);       //生成：雅可比矩阵      jac = invert(jac);//生成：雅可比矩阵的逆      deriv = matmul(der, jac);//生成：整体坐标下形函数的偏导数      bee = beemat(nst, ndof, deriv);//生成：应变-位移矩阵[B]      eps = matmul(bee, eld);//生成：单元应变向量      sigma = matmul(dee, eps);//生成：单元应力向量      fout << setw(14) << scientific << setprecision(4) << gc[0]           << setw(14) << scientific << setprecision(4) << sigma[0]           << setw(14) << scientific << setprecision(4) << sigma[3] << endl;      cout << setw(14) << scientific << setprecision(4) << gc[0]           << setw(14) << scientific << setprecision(4) << sigma[0]           << setw(14) << scientific << setprecision(4) << sigma[3] << endl;      fout << "    " << setw(14) << scientific << setprecision(4) << gc[1]                     << setw(14) << scientific << setprecision(4) << sigma[1]                     << setw(14) << scientific << setprecision(4) << sigma[4] << endl;      cout << "    " << setw(14) << scientific << setprecision(4) << gc[1]                     << setw(14) << scientific << setprecision(4) << sigma[1]                     << setw(14) << scientific << setprecision(4) << sigma[4] << endl;      fout << "    " << setw(14) << scientific << setprecision(4) << gc[2]                     << setw(14) << scientific << setprecision(4) << sigma[2]                     << setw(14) << scientific << setprecision(4) << sigma[5] << endl;      cout << "    " << setw(14) << scientific << setprecision(4) << gc[2]                     << setw(14) << scientific << setprecision(4) << sigma[2]                     << setw(14) << scientific << setprecision(4) << sigma[5] << endl;    }  }}


  主程序可用于三维有限元静力分析，六面体单元(网格)，考虑外加荷载和边界条件。涉及到的子程序/函数有8类：

  1. 高斯积分法与形函数：sample()，shape_fun()，shape_der()；
  2. 单元刚度矩阵：beemat()，deemat()；
  3. 单元定位：num_to_g()，formnf()；
  4. 网格生成：mesh_size()，hexahedron_xz()；
  5. 文件流与命名：getname();
  6. 矩阵计算：transpose()，matmul()，determinant()，invert()；
  7. 迭代收敛判断：checon();
  8. 前后处理可视化：mesh_ensi()，dis msh_ensi()。

第1~2类子程序/函数源码可参照以下4篇文章：

第3~5类子程序/函数源码可参照以下1篇文章：

第6类子程序/函数源码可参照以下1篇文章：

第7类子程序/函数源码可参照以下1篇文章：

第8类子程序/函数源码可参照以下4篇文章：

特别提示：CG子程序/函数源码可参照以下4篇文章：


5. 数值案例

5.1. 案例一：立方弹性实体


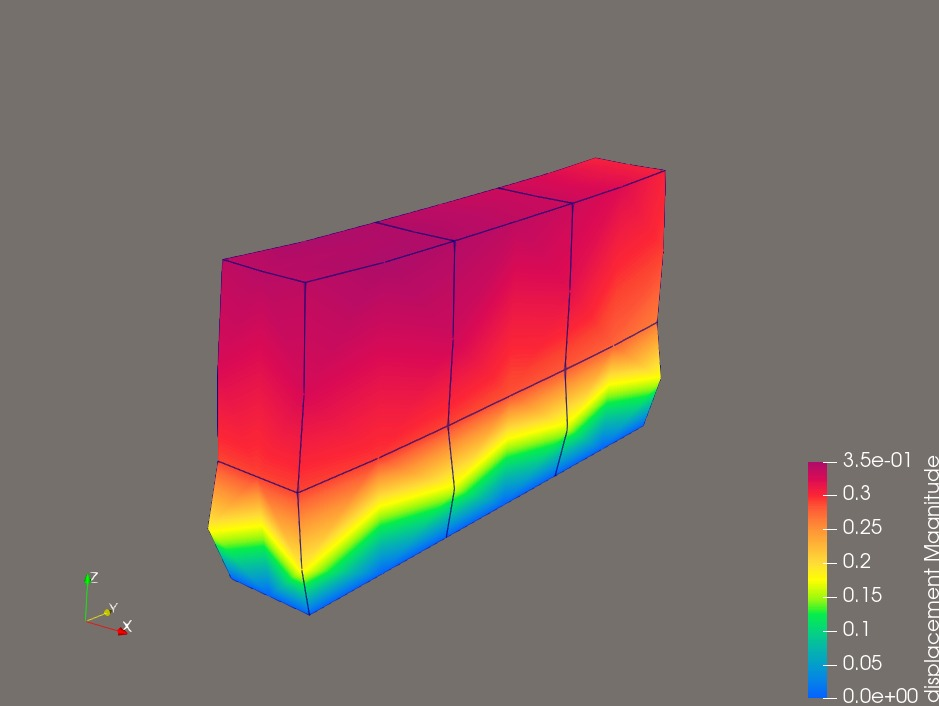
图2：位移云图-立方弹性实体-考虑重力荷载

  上图的“大西瓜”是不是很好吃啊？该案例曾经在《考虑重力荷载的二维/三维有限元分析C++编程实现》详细讨论过，当时采用直接算法（Cholesky分解）求解有限元方程。

  这次改用PCG迭代算法，也就是Jacobi预处理的逐个单元法（EBE）。网格划分和其他数据输入，均沿用上次直接算法的方案和信息。PCG迭代次数上限和收敛容差，分别赋值为200和1.0e-5。

  理论上最多124次迭代即可收敛，实际上61次迭代（无预处理增加至73次），得到较为满意的计算结果，和直接算法几乎是一模一样，精确啊。所以，这里就不再展示结果数据和云图了，反正都一样。

  随着问题规模的扩大，迭代法相对于直接法的优势更显著，但也有其适用条件。请看↓↓下一个案例↓↓

5.2. 案例二：悬臂钢梁

  求出下图所示的悬臂钢梁在角点处的挠度。


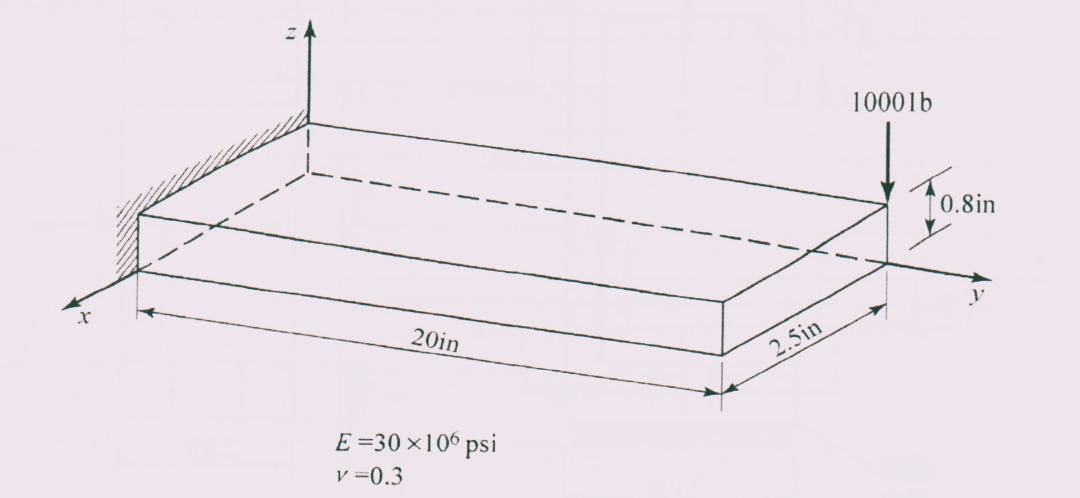
图3：悬臂钢梁

  本案例曾经在《六面体单元与弹性实体的三维有限元分析C++编程实现》闪亮登场。
这次沿用其网格划分方式：采用20节点六面体缩减积分单元来划分网格，各单元/网格尺寸不大于1.0in，x、y、z方向的单元数分别为3、20、1。固定端18个节点3个维度的自由度均为0，自由端角点承受集中荷载1000lb竖直向下。
  将PCG迭代次数上限赋值为2000（本案例理论值是1560）；将PCG收敛容差赋值为1.0e-10，由于直接法求得解向量的数量级从1.0e-2到1.0e-15跨越较大，在计算开销和结果精度之间综合考虑性价比。输入数据*.dat文件的相关内容如下：

==================================
  数值案例：悬臂钢梁结构的数据输入  
==================================    

单元节点数nod
20

各方向单元数nxe/nye/nze
3    20    1

单元积分节点数nip
8

PCG收敛误差/迭代上限
1.0e-10    2000

材料类型数np_types
单元特征值prop(弹性模量e, 泊松比v)
1
3.0e7    0.3

单元特性类型etype(不需要not needed)

网格布置的x向坐标x_coords
 0.0  0.8333  1.6667  2.5

网格布置的y向坐标y_coords 
 0.0  1.0  2.0  3.0  4.0  5.0  6.0
 7.0  8.0  9.0 10.0 11.0 12.0 13.0
14.0 15.0 16.0 17.0 18.0 19.0 20.0

网格布置的z向坐标z_coords
 0.0 -0.8

约束节点数nr
约束节点编号k1与相应的自由度nf
18
521 0 0 0  522 0 0 0  523 0 0 0  524 0 0 0  525 0 0 0  526 0 0 0
527 0 0 0  528 0 0 0  529 0 0 0  530 0 0 0  531 0 0 0  532 0 0 0
533 0 0 0  534 0 0 0  535 0 0 0  536 0 0 0  537 0 0 0  538 0 0 0

受载节点数loaded_nodes
受载节点编号k2与相应的荷载loads
1
7  0.0  0.0 -1000.0

给定位移数fixed_freedoms
0

  采用本文程序读入*.dat文件，得到计算结果*.res如下。

===============================================
    数值案例：悬臂钢梁结构的节点位移和单元应力
===============================================

 There are 1560 equations.
 Number of pcg iterations to convergence was 1117.

 Node     x-disp        y-disp        z-disp
   1    2.3545e-03   -2.4607e-02   -8.1387e-01
   2    2.3695e-03   -2.4628e-02   -8.1634e-01
   3    2.3927e-03   -2.4664e-02   -8.1887e-01
   4    2.3776e-03   -2.4676e-02   -8.2135e-01
   5    2.3719e-03   -2.4702e-02   -8.2391e-01
   6    2.4998e-03   -2.4931e-02   -8.2662e-01
   7    2.6770e-03   -2.5091e-02   -8.2986e-01
   8    6.5918e-06   -1.7195e-06   -8.1387e-01
   9   -6.8897e-06    4.1039e-06   -8.1884e-01
  10    2.6237e-05   -7.3709e-06   -8.2394e-01
  11   -5.2107e-05    4.3864e-05   -8.2931e-01
  12   -2.3790e-03    2.4618e-02   -8.1386e-01
  13   -2.3658e-03    2.4622e-02   -8.1635e-01
  14   -2.3625e-03    2.4641e-02   -8.1882e-01
  15   -2.4004e-03    2.4700e-02   -8.2138e-01
  16   -2.4321e-03    2.4791e-02   -8.2394e-01
  17   -2.4056e-03    2.4816e-02   -8.2657e-01
  18   -2.3319e-03    2.4775e-02   -8.2887e-01
 ...
    <此处省略一万字>
 ...
 520    5.2912e-04    1.0342e-03   -4.1442e-04
 521    0.0000e+00    0.0000e+00    0.0000e+00
 522    0.0000e+00    0.0000e+00    0.0000e+00
 523    0.0000e+00    0.0000e+00    0.0000e+00
 524    0.0000e+00    0.0000e+00    0.0000e+00
 525    0.0000e+00    0.0000e+00    0.0000e+00
 526    0.0000e+00    0.0000e+00    0.0000e+00
 527    0.0000e+00    0.0000e+00    0.0000e+00
 528    0.0000e+00    0.0000e+00    0.0000e+00
 529    0.0000e+00    0.0000e+00    0.0000e+00
 530    0.0000e+00    0.0000e+00    0.0000e+00
 531    0.0000e+00    0.0000e+00    0.0000e+00
 532    0.0000e+00    0.0000e+00    0.0000e+00
 533    0.0000e+00    0.0000e+00    0.0000e+00
 534    0.0000e+00    0.0000e+00    0.0000e+00
 535    0.0000e+00    0.0000e+00    0.0000e+00
 536    0.0000e+00    0.0000e+00    0.0000e+00
 537    0.0000e+00    0.0000e+00    0.0000e+00
 538    0.0000e+00    0.0000e+00    0.0000e+00

 The integration point (nip=1) stresses are:
 Element  x-coord       sig_x         tau_xy
          y-coord       sig_y         tau_yz
          z-coord       sig_z         tau_zx
   1    4.1665e-01   -1.6922e+02    7.4603e+01
        5.0000e-01   -2.1058e+01    1.2518e+02
       -4.0000e-01    2.6853e+02    7.1402e+01
   2    1.2500e+00    4.9339e+02   -2.5319e+02
        5.0000e-01    2.5986e+02    1.6048e+02
       -4.0000e-01   -6.0067e+02   -6.8331e+01
   3    2.0834e+00    2.3960e+02    1.1597e+03
        5.0000e-01    5.3165e+02    1.5338e+02
       -4.0000e-01    4.4750e+03    3.5539e+02
   4    4.1665e-01    3.4916e+01   -1.1448e+01
        1.5000e+00    2.9443e+01    1.6057e+02
       -4.0000e-01    5.2932e+00    2.6655e+01
   5    1.2500e+00   -2.7901e+02    4.8352e+01
        1.5000e+00   -2.4874e+02    2.0400e+02
       -4.0000e-01   -1.7001e+02    3.6931e+01
   6    2.0834e+00    5.2750e+02   -2.2657e+02
        1.5000e+00    5.0020e+02    5.5917e+02
       -4.0000e-01   -2.6498e+02   -3.2220e+01
  ...
    <此处省略一万字>
  ...
  55    4.1665e-01   -1.3728e-04    9.9451e-05
        1.8500e+01    8.5541e-04    1.5749e+02
       -4.0000e-01   -2.7138e-04    2.0642e+02
  56    1.2500e+00   -1.0924e-04    4.8649e-05
        1.8500e+01    6.3818e-04    1.1273e+03
       -4.0000e-01    1.4572e-04    1.0028e+02
  57    2.0834e+00   -7.5297e-04    3.3840e-06
        1.8500e+01    3.2310e-04    6.3619e+02
       -4.0000e-01   -3.5304e-04   -1.1781e+02
  58    4.1665e-01    4.8693e-04   -2.0624e-04
        1.9500e+01    1.0268e-03   -1.3259e+02
       -4.0000e-01    6.3731e-04    2.1773e+03
  59    1.2500e+00    5.2539e-04    5.7990e-05
        1.9500e+01    1.2485e-03    2.5447e+03
       -4.0000e-01    1.5490e-04    3.8806e+02
  60    2.0834e+00   -5.0271e-04    8.1129e-05
        1.9500e+01    9.0502e-04    8.1519e+02
       -4.0000e-01   -1.1469e-03   -1.9705e+03

  经过1117次PCG迭代（无预处理CG迭代增加到1436次），得到该悬臂结构的自由端位移（节点7的z向位移）为-8.2986e-1in，与直接算法的结果一致。从结果数据可以看出，在收敛容差1.0e-10的前提下，精度不超过1.0e-8的位移值，以及精度不超过1.0e-3荷载值，满足预期要求。迭代法的短板啊。但是，多快好省是强项，不容置疑。

  采用本文算法自动生成EnSight Gold后处理文件，通过ParaView查看位移云图如下图所示。图中透明实体为初始（未变形）悬臂钢梁，蓝色向下箭头为自由端集中荷载。迭代算法和直接算法的位移云图几乎是重叠的。


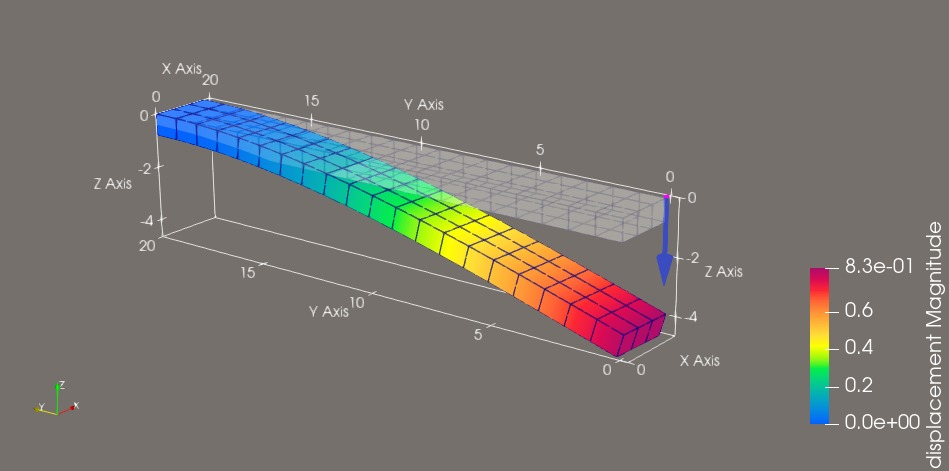
图4：位移云图-迭代算法-悬臂钢梁


6. 讨论

  本文采用迭代法求解有限元方程，优势是计算效率高+内存消耗低；但是精确度不如直接法。基于PCG的逐个单元法（EBE），通过Jacobi预处理技术，改善系数矩阵的条件数，加速收敛速度；至于IC、SSOR等预处理方案，大家可以试试啊。

  下面这个表格对比直接法和迭代法的核心区别。

对比维度    
直接法迭代法
核心原理
通过有限步精确的矩阵运算（如消元、分解）直接得到理论上的精确解。    
从一个初始猜测解出发，通过迭代公式不断逼近真实解，得到的是满足精度要求的近似解。    
收敛性无条件收敛（只要矩阵非奇异），结果具有确定性。收敛性有条件，依赖于系数矩阵的性质（如谱半径＜1），可能发散或收敛慢。
计算效率
时间复杂度通常为O(n³)，适合中小规模问题。对多右端项问题优势明显。    
每步迭代复杂度可低至近O(n)，适合大规模稀疏问题。但收敛速度影响总时间。    
内存消耗
需要存储完整的矩阵及其分解因子，内存开销较大，高达O(n²)。    
仅需存储非零元素和少量中间向量，内存效率高，可低至O(n)，特别适合大型稀疏矩阵。    
数值稳定性
稳定性较高，尤其在使用主元选择技术后。    
对病态矩阵非常敏感，收敛速度会急剧下降，甚至失败。    
主要方法
高斯消去法、LU分解、Cholesky分解（针对对称正定矩阵）。    
Jacobi迭代、Gauss-Seidel迭代、共轭梯度法(CG)、GMRES等。    
典型应用场景
中小规模稠密矩阵问题；多工况分析；对精度要求极高的关键计算。    
大型稀疏系统（如有限元法、计算流体力学）；网格规模极大、内存受限的场景。    

  直接法是确定性高精度解的首选，迭代法是大规模问题的必然选择。在工程实践中，选择的本质是在精度、效率与可靠性之间寻找动态平衡——这恰是数值方法的魅力所在。稀疏矩阵+并行处理，计算效率进一步飞升，敬请期待。

参考文献：

  • [1]: Gene H. Golub, Charles F. Van Loan 著. 程晓亮 译. 矩阵计算(原书第4版)[M]. 北京: 人民邮电出版社, 2020
  • [2]: T. Sauer 著. 裴玉茹, 马赓宇 译. 数值分析(原书第2版)[M]. 北京：机械工业出版社, 2014
  • [3]: I. M. S mith, D. V. Griffiths, L. Margetts 著. 张新春, 慈铁军, 范伟丽 等译. 有限元方法编程(原书第五版)[M]. 北京: 电子工业出版社, 2017
  • [4]: T. R. Chandrupatla, A. D. Belegundu 著. 曾攀, 雷丽萍 译. 工程中的有限元法(原书第四版)[M]. 北京：机械工业出版社, 2021


来源：有限元先生
EnSight非线性电子ADSCONVERGEUGUM理论材料
著作权归作者所有，欢迎分享，未经许可，不得转载
首次发布时间：2025-10-26
最近编辑：3小时前
外太空土豆儿
外太空土豆儿
博士 我们穷极一生，究竟在追寻什么？
获赞 41粉丝 37文章 90课程 0
点赞
收藏
作者推荐

文献分享：基于SBFEM-USM的三维弹塑性分析框架及其在ABAQUS中的实现

摘要  本研究针对三维弹塑性分析，提出了一种基于均匀应变法（Flanagan and Belytschko, 1981）和比例边界有限元法（SBFEM）的改进计算框架。SBFEM作为一种支持任意形状多面体单元的数值方法，新框架通过采用单元平均应变策略，结合八叉树分解算法实现了高分辨率图像与复杂STL格式几何模型的自动网格转化，生成满足共形性与平衡性要求的八叉树网格。该框架创新性地融合了144种独特的八叉树单元模式（Zhang et al., 2021），通过推导单元模式的旋转、镜像与缩放操作流程，显著优化了弹塑性分析的工作流程并提升计算效率。本方法以UELMAT用户单元形式在ABAQUS平台中实现，可直接调用内置材料库。通过涵盖八叉树单元与任意形状比例边界有限元的四个验证算例，系统考察了计算精度、收敛速率与运算效率。结果表明：该框架有效规避了体积闭锁现象，较现有方法实现4倍加速，计算速度与ABAQUS内置单元相当。最后以钢试样图像压缩分析及口腔结构接触分析为例，验证了自动化工作流程的可行性与计算速度的显著提升。研究框架与技术突破1. 核心问题背景传统局限：基于图像的弹塑性分析需将CT/STL数据转换为CAD格式，高分辨率模型处理耗时可达数周（Section 1）SBFEM优势：仅需边界离散，域内解析求解，天然支持多面体单元2. 关键技术创新(1) 均匀应变法融合应变场分解： Δε = Δε̄ + Δε̃ （式35） 其中ε̄为单元平均应变（控制材料响应），ε̃为波动应变（稳定数值解）解决体积闭锁问题：在近不可压缩材料（ν=0.49995）中保持精度（Section 5.4）(2) 八叉树模式库优化预计算144种单元模式的刚度分量矩阵**Hkl**（式65-66）通过旋转/镜像操作复用模式，内存占用降低80%（Section 4）3. ABAQUS集成实现UELMAT用户单元：支持von Mises等6种弹塑性模型流程图：算例验证：精度与效率分析1. 基础验证：单元与基准测试(1) 单单元拉伸模型：17节点八叉树单元受单轴拉伸（图3a）结果：应力误差&lt; 10-12 MPa（表1）(2) 多单元基准测试模型：7单元多面体网格（图5b）结果：节点位移相对误差达机器精度（表2）2. 工业标准模型：Cook板问题模型：悬臂板受剪切载荷（图7）关键结果：单调载荷：von Mises应力分布匹配参考解（图9）循环载荷：位移响应误差&lt;1.5%（图12）3. 近不可压缩材料验证模型：立方体（E=250 GPa, ν=0.49995）受局部压力（图13）定量结果： 收敛性：位移误差随DOF增加指数下降（图16）计算效率：较四面体单元提升70%（图17）加速比：较传统方法[73]提升4.76倍（表4）4. 工程应用验证  牙齿咬合接触，2,330,589自由度，切牙接触区塑性应变，非线性响应吻合工程价值与开源资源1. 方法论意义首创SBFEM-USM在近不可压缩材料中的稳定求解方案八叉树预计算将刚度矩阵复杂度从O(n)降至O(1)2. 工业应用前景材料科学：3D打印件微观结构分析生物力学：种植牙载荷评估工业检测：腐蚀构件剩余寿命预测3. 开源资源代码仓库：https://gitlab.com/seanyc.public/sbfem-uelmat-for-plasticity包含：- ABAQUS UELMAT实现- Cook膜/立方体验证案例- 程序说明 来源：有限元先生

未登录
还没有评论
课程
培训
服务
行家
有问必答第2期-无主题自由问答专场【直播回放】 ALIAS汽车设计职业培训班-汽车A面从入门到精通（提高班-持续加餐更新）国产自主工业软件行业洞察2022第4期：云化架构仿真产品和平台在航空航天领域的应用实践Ansys有限元医学及生物力学仿真综合专题——口腔专业
相关推荐
ABAQUS Python二次开发第三季(超级后处理篇)飞行器结构设计之铆钉有限元计算应用（回放）ABAQUS细观混凝土骨料砂浆ITZ三相建模(Python二次开发)如何成为电声高手-COMSOL声学仿真32讲：助你构建声学产品工程师知识体系
最新文章
Actran 基础案例 | 点声源计算
面向制造和装配的设计？-- 你可能误解了DFMA的真正含义
汽车电子硬件设计时钟信号EMI降低方法
信噪比：通信链路设计的理论基础
赢合科技亮相北美电池展，创新智造深度赋能全球新能源产业！
热门文章
通用/泛亚/蔚来/弗迪/上海电驱动等百位新能源专家确认发言，易贸三电活动6月苏州见
一种降低电池温差的装置
Fluent湍流模型中壁面函数选择建议
湍流与涡流的区别
涡结构提取
其他人都在看
破解供应链困局：达索系统助力包装消费品与零售行业的APS升级
“苏超”超级拉动民间消费！
基于DeepSeek+Python回归分析的SolidWorks仿真变形值预测
动力电池产线大揭秘：一文吃透制造全流程！
全球新能源大变局下，长时储能何以成为决胜关键！
VIP会员 学习计划 福利任务
下载APP
联系我们
帮助与反馈