永磁同步电机PMSM模型预测控制MPC关键技术系列专题—MPTC单、双矢量控制性能对比
导读:本系列主要介绍永磁同步电机模型预测控制,参考张晓光教授编写的参考书《永磁同步电机模型预测控制》。此系列主要介绍模型预测转矩控制MPTC、模型预测电流控制MPCC和模型预测磁链控制MPFC。
研究和复现单矢量和多矢量MPC控制的实现,以及延时补偿等涉及的关键技术。通过MATLAB仿真验证和后续在TI控制实验平台上进行测试。
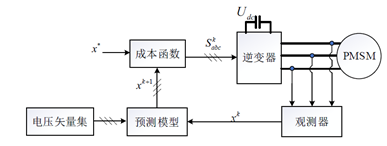
图1 永磁同步电机模型预测控制系统框图
一、模型预测控制发展概述
模型预测控制 (MPC) 又称为滚动时域控制( RHC),是20 世纪 70 年代后期出现于工业工程控制领域的一类计算机控制算法,在化工等过程控制行业得到了广泛应用。由于MPC 的本质是求解一个开环最优控制问题,因此计算量较大,而电力电子与电机控制对控制的实时性要求较高,过去受制于微处理器的计算能力,MPC 在电力电子与电力传动领域鲜有实际应用。1983 年 Holtz J 等人首先提出在电力传动领域中应用模型预测控制的思想,但由于预测控制计算量较大,受制于当时的硬件成本,并未引起广泛关注。直到近年来随着数字信号处理器(DSP)计算性能的大幅提升和价格的不断降低,在低成本硬件处理器上实现各种复杂控制算法成为可能。MPC 以其原理简单、多变量控制和容易处理非线性约束等优点,吸引了众多学者对其在电力传动领域中的应用进行研究。
一般工业过程中存在多变量耦合、非线性以及不确定性等问题,很难建立准确的模型。因此,采用经典PID 控制器或者是一些传统的控制算法所得到的效果并不理想,存在一定的局限性。MPC 最突出的特点是“边走边优化”,且对模型的精确性要求较低,因此能够有效地用于复杂对象的控制。
二、模型预测控制MPC控制原理介绍
模型预测控制应用于电气传动系统中时,可分为连续控制集模型预测控制( CCS-MPC)和有限控制集模型预测控制 ( FCS-MPC) 。两者的主要区别: ( 1) 优化方式不同;CCS-MPC利用数学工具对价值函数求最优解得到最优控制量; 而FCS-MPC 利用变换器的离散性和有限性,遍历电压矢量,价值函数最小的电压矢量即最优控制量。( 2) 作用方式不同;CCS-MPC 中控制量是通过脉冲宽度调制( PWM) 方式作用于系统; 而FCS-MPC中控制量直接作用于系统。与CCS-MPC相比,FCS-MPC 将目标优化和开关状态决策过程优化成一步,且具有概念简单、适用范围广、约束和非线性易纳入价值函数等优点,因此成为了近年来的研究热点之一。
2.1模型预测控制MPC原理
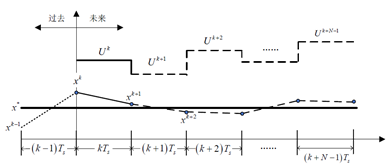
图2 模型预测控制时序图
MPC的具体描述为:在采样信息的基础上,预测得到固定时域长度内的被控对象状态变量和输出变量轨迹,然后构造相应的价值函数,通过滚动优化在线求解价值函数,得到系统最优输入变量序列,实现系统的优化控制。
采样信息指的是定子电压、定子电流,作为磁链观测器的输入,预测得到状态变量(比如采用的是全阶磁链观测器,状态变量为定子电流和定子磁链),然后预测得到转矩,最后构造价值函数,通过滚动优化(有八个电压矢量参与计算)在线求解价值函数,最优解就是价值函数值最小的对应的电压矢量,将最优的电压矢量开关序列给到逆变器完成控制。(选取最优解的目的:使图2中的输出变量最贴近参考值)。
2.2 模型预测
什么叫预测模型?预测模型是使用观测器,利用当前时刻的电压、电流去计算下一时刻的值代入到计算中,所以使用的观测器就叫预测模型。
为了在DSP控制系统中对下一时刻的定子磁链以及转矩进行预测,首先需要对全阶磁链观测器(状态变量是定子电流和定子磁链)进行离散化处理,为了获取较好的预测精度,本文采用梯形积分法,公式如下:
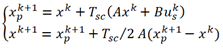
为什么要进行离散化处理?在全数字化驱动系统中,预测模型(磁链观测器)是通过微处理器实现的,连续的预测模型必须经过离散化处理,所以预测模型的离散化技术十分关键,对于实际工程应用非常有意义。离散化技术包括:离散化方法、离散步长的选择和离散预测模型稳定性分析。离散化过程对预测模型的性能影响较大,其不仅影响预测模型的动态性能,还影响稳态精度,甚至在部分区域会导致预测模型发散。
2.3 代价函数的构造
本文希望在保持定子磁链幅值恒定的情况下控制转矩快速跟踪指令值,故构造目标函数图下:
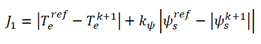
需要说明的是,上式只是权重系数的初始设置值,在实际应用中还需要根据实际实验进行调整。
为了获取高性能的控制效果,需要设计合适的权重系数,但是到目前为止,权重系数的设计都是通过经验与仿真得到的,缺乏必要的理论基础。因此在实际应用中,传统的MPTC具有一定的局限性。
三、模型预测转矩控制单、双矢量控制性能对比
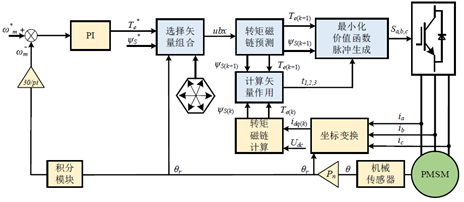
图3 永磁同步电机模型预测转矩控制MPTC框图
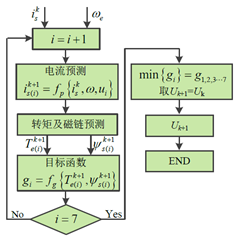
图4 单矢量MPTC控制流程图
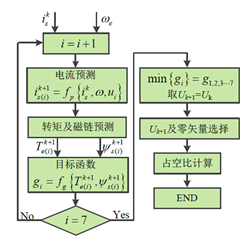
图5 双矢量MPTC控制流程图
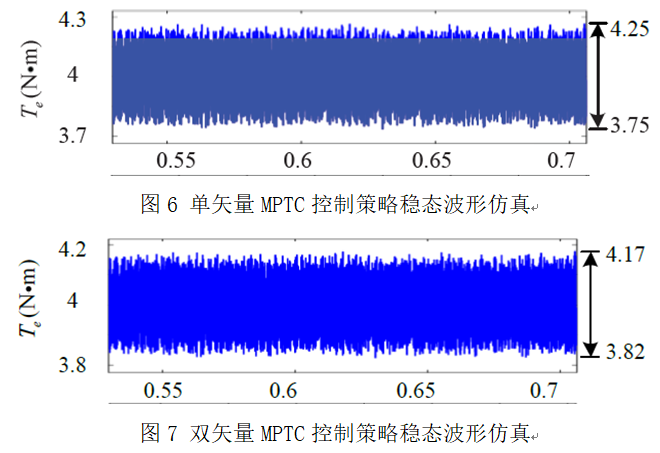
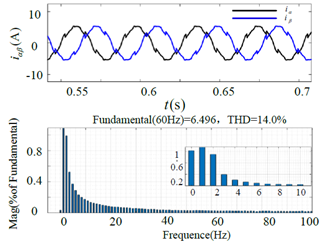
图8 单矢量MPTC控制策略电流FFT分析波形
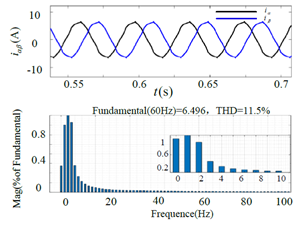
图9双矢量MPTC控制策略电流FFT分析波形
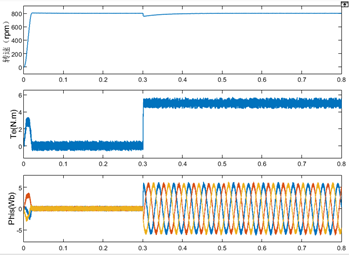
图10 单矢量MPTC控制策略动态仿真波形
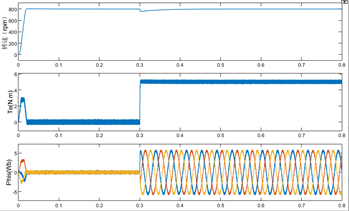
图11双矢量MPTC控制策略动态仿真波形
根据前面对单矢量MPTC的研究可知,单矢量MPTC在整个控制周期内只有一个基本电压矢量作用。因此转矩脉动比较大,系统的稳态性能较差,为了提高系统的稳定性能,可以在一个控制周期内使两个基本电压矢量作用,即双矢量模型预测转矩控制。目前双矢量MPTC主要有两种形式:一种是基于占空比控制的模型预测转矩控制;另一种是任意双矢量模型预测转矩控制。基于占空比控制的模型预测转矩控制在一个控制周期内作用一个有效电压矢量和一个零电压矢量。任意双矢量模型预测转矩控制在一个控制周期内作用任意两个电压矢量。从本质上讲,基于占空比控制的模型预测转矩控制是一种特殊的任意双矢量模型预测转矩控制,只是其双矢量组合的方式受到了限制。这两种策略的控制性能在低速区间是基本一致的,在高速区间任意双矢量模型预测转矩控制具有更加优越的稳态性能。
四、问题总结与讨论
1、占空比的计算,一般采用什么计算方式?
2、双矢量的MPC发波应该如何实现?
3、代价函数中的权重系数该如何确定?
来源:浅谈电机控制





