Monte Carlo 生成特定分布实例演示

1年前浏览1506

过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载，**：927550334

过冷水在往期文章中和大家一起学习Matlab生成任意分布数据实例演示，比较熟悉统计分布的读者可看出用实际工作中是用的Monte Carlo做随机分布的生成，

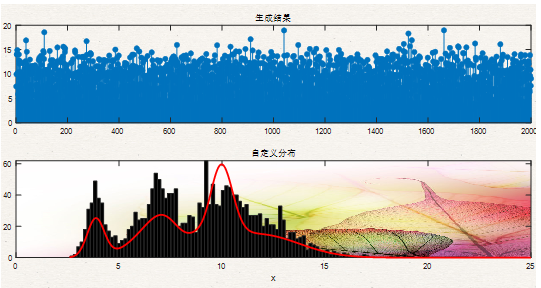
黑色柱状图是目标分布，红线是采用蒙特卡洛生成的分布，Monte Carlo分布和黑色分布只是形式相近，真正和黑色分布的贴合程度有限，一个是条状图，一个是伪概率密度分布函数，还有一个很根本的问题，条状图和概率密度分布图的数据量不一样。本期过冷水就和大家进阶学习一下用Monte Carlo完全复刻柱状分布。

柱状分布是过冷水在做一个小盒中两两小球的相对位置距离分布，首先小盒中有54个原子

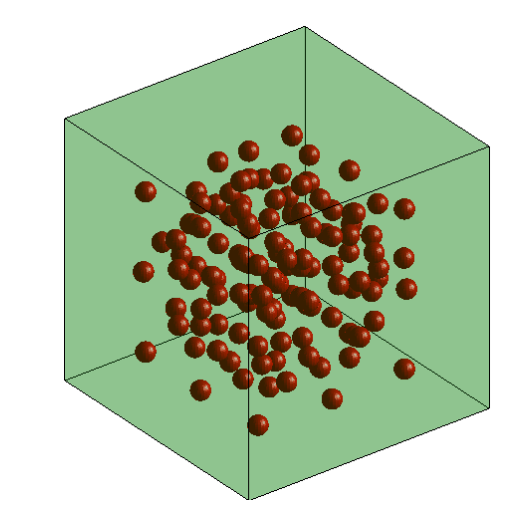
54个原子坐标数据是最初始的数据，我们需要的两两原子之间的坐标距离，共获得54*53个距离数据，因为绘制的是柱状图，同时需要对坐标数据做区间划分，对应处理程序为：

data=[0,0,0;2.17497659055443,2.17497659055443,2.17497659055443;4.34982299830278,0,0;6.52479982375000,2.17497659055443,2.17497659055443;8.69977664919722,0,0;10.8746223392176,2.17497659055443,2.17497659055443;0,4.34982299830278,0;2.17497659055443,6.52479982375000,2.17497659055443;4.34982299830278,4.34982299830278,0;6.52479982375000,6.52479982375000,2.17497659055443;8.69977664919722,4.34982299830278,0;10.8746223392176,6.52479982375000,2.17497659055443;0,8.69977664919722,0;2.17497659055443,10.8746223392176,2.17497659055443;4.34982299830278,8.69977664919722,0;6.52479982375000,10.8746223392176,2.17497659055443;8.69977664919722,8.69977664919722,0;10.8746223392176,10.8746223392176,2.17497659055443;0,0,4.34982299830278;2.17497659055443,2.17497659055443,6.52479982375000;4.34982299830278,0,4.34982299830278;6.52479982375000,2.17497659055443,6.52479982375000;8.69977664919722,0,4.34982299830278;10.8746223392176,2.17497659055443,6.52479982375000;0,4.34982299830278,4.34982299830278;2.17497659055443,6.52479982375000,6.52479982375000;4.34982299830278,4.34982299830278,4.34982299830278;6.52479982375000,6.52479982375000,6.52479982375000;8.69977664919722,4.34982299830278,4.34982299830278;10.8746223392176,6.52479982375000,6.52479982375000;0,8.69977664919722,4.34982299830278;2.17497659055443,10.8746223392176,6.52479982375000;4.34982299830278,8.69977664919722,4.34982299830278;6.52479982375000,10.8746223392176,6.52479982375000;8.69977664919722,8.69977664919722,4.34982299830278;10.8746223392176,10.8746223392176,6.52479982375000;0,0,8.69977664919722;2.17497659055443,2.17497659055443,10.8746223392176;4.34982299830278,0,8.69977664919722;6.52479982375000,2.17497659055443,10.8746223392176;8.69977664919722,0,8.69977664919722;10.8746223392176,2.17497659055443,10.8746223392176;0,4.34982299830278,8.69977664919722;2.17497659055443,6.52479982375000,10.8746223392176;4.34982299830278,4.34982299830278,8.69977664919722;6.52479982375000,6.52479982375000,10.8746223392176;8.69977664919722,4.34982299830278,8.69977664919722;10.8746223392176,6.52479982375000,10.8746223392176;0,8.69977664919722,8.69977664919722;2.17497659055443,10.8746223392176,10.8746223392176;4.34982299830278,8.69977664919722,8.69977664919722;6.52479982375000,10.8746223392176,10.8746223392176;8.69977664919722,8.69977664919722,8.69977664919722;10.8746223392176,10.8746223392176,10.8746223392176]./13.0495996474999991
dr=0.002;Distance1=[];
for i=1:54
        dataj=data;
        dataj(i,:)=[];
distance=sqrt((data(i,1)-dataj(:,1)).^2 (data(i,2)-dataj(:,2)).^2 (da
ta(i,3)-dataj(:,3)).^2);
        Distance1=[Distance1;round(distance/dr)];
end

得到 Distance1就是用于绘制分布的数据，其不是直接的坐标数据，因为坐标数据离散度太大，不太容易绘制条形图，需要对其做化区间处理，所以Distance1是一个间隔为dr的区间统计表，得到的 Distance1用histogram函数绘图。

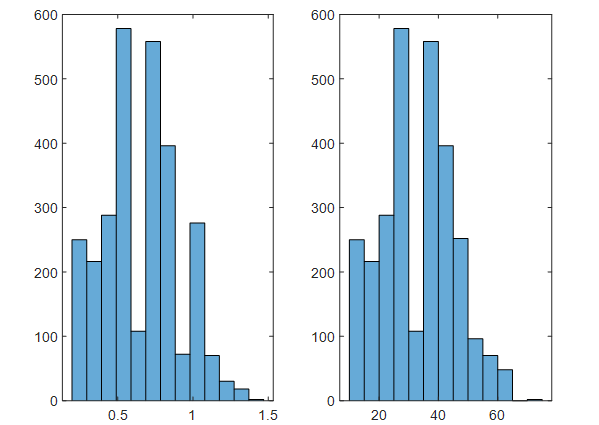
figure
subplot(1,2,1)
A=histogram(Distance,'BinWidth',0.098)
subplot(1,2,2)
b=histogram(Distance1,'BinWidth',5)

我们要做点就是用Monte Carlo方法生成一组data_monte-Carlo数据使之分布和data分布一致,在这个过程中过冷水想了很多种办法生成data_monte-Carlo坐标集。

（1）随机生成54个三维坐标数据，用这些坐标算出Distance1_Monte-Carlo，将Distance1作为目标函数判断，仿照生成概率密度分布函数的方法来做，

Distance11=[];
while ~isequal(Distance11,Distance1)
    data=rand(54,3);
    for i=1:54
        dataj=data;
        dataj(i,:)=[];
        distance =sqrt((data(i,1)-dataj(:,1)).^2 (data(i,2)-dataj(:,2)).^2 (data(i,3)-dataj(:,3)).^2);
        Distance11=[Distance11;round(distance/dr)];
    end
end

当过冷水将相应程序写出来运行后发现程序运行一直无法跳出循环，随即发现这竟然是一个3^54维判断问题，使用随机命令自然很难找到满足目标分布的坐标。

（2）方案一失败原因是因维度过高，自然就想到要降低问题维度,不能一次性生成54个坐标数据，那么就一个坐标一个坐标数据生成，这样思路就相当于每次都是解一个三维问题，自然会轻松很多，那么问题如何判断每次生成的坐标都是符号要去的呢？还是需要目标函数做判断，而且不同原子数的分布不同，目标函数应该不同。既然有2862个坐标数据，自然想到用其作为目标判断函数，于是过冷水就做了这么一个判断：要想54个原子满足特定分布,则2个原子情况下的满足A1分布，在两个原子满足A1分布条件下，3个原子需要满足A2分布，同理可得A3,...A54分布，A54分布就是我们的目标分布，反向推导分布简直完美。

F=sort(Distance1);
B=rand(1,3)
dataA=rand(1,3);
data1=[dataA;B];
[m,n]=size(data1)
Distance11=rand(m*(m-1),1);
for k=1:53
    B=rand(1,3);
    dataA=data1;
    data1=[dataA;B];
    [m,n]=size(data1);
    Distance11=rand(m*(m-1),1);
while ~isequal(Distance11,F(1:m*(m-1)));
    B=rand(1,3); % B=13.0495996474999991*rand(1,3)
    data1=[dataA;B];
    Distance11=[];
    for i=1:m
         dataj=data1;
         dataj(i,:)=[];
         distance =sqrt((data1(i,1)-dataj(:,1)).^2 (data1(i,2)-dataj(:,2)).^2 (data1(i,3)-dataj(:,3)).^2);
         Distance11=[Distance11;round(distance/dr)];
    end  
end
end

每次都只有求一个坐标的分布，利用Matlab的随机命令非常简单，问题在于A1,...A54目标分布该如何建立？过冷水将2862个坐标数据按照，2*3,3*4,4*5生成目标分布，然后写出相应程序，在实践中发现满足当程序运行到一定程度后在满足A40坐标情况下很难在生成满足A41的分布，过冷水当时可难受了，思路明明是正确的为什么无法生成目标满足目标的目标函数，经反复思索,从A54,反推A1这个过程出了问题，在生成随机分布过程中满足A4(四原子)的分布的情况可能有五种，其中有三种可能会导致其不满足A54,分布，可是在生成A4,A5的分布又不会报错，当发现在Ai基础上不能再生成Ai 1情况下，是没有办法核验分布的，该想法的思路有问题的地方是在于过冷水认为一个原子一个个，没有原子都给其一个分布用于可是由于约束过多反而导致分布之间相互矛盾，

(3) 当发现在Ai基础上不能再生成Ai 1情况下，是没有办法核验分布的，该想法的思路有问题的地方是在于过冷水认为给原子应该满足的分布约束条件太多，没个原子都给其一个分布，可是由于约束过多反而导致分布之间相互矛盾，所以过来水不能对第i个原子指定特定分布，约束其可能出现位置，应该采取方式A1,A2，A3,A4，A54合成一个目标函数A54，只要原子分布<A54,就可以认为原子集是正确的，如果可以生成下一个分布，如果不可以重新生成一个原子坐标。这样的话就可以生成54个坐标，最后的坐标为就是满足A54的分布，

addnumber=sort([Distance1;repmat(unique(Distance1),20,1)]);
date_coord_length=1;date_coordination=[];
for date_coord_length=1:2
intcoord=round(rand(1,3),3);
n=5000;dr=0.002;
while length(intcoord)<54
coord=intcoord;
assemble=cell(n,1);length_assemble=1;
while length_assemble<=n
   init_assemble=intcoord(1,:);
    while ~all(round((sqrt((init_assemble(1,1)-coord(:,1)).^2 (init_assemble(1,2)- coord(:,2)).^2 (init_assemble(1,3)- coord(:,3)).^2))./dr)<min(Distance1) ==0)|~all((max(Distance1)<round((sqrt((init_assemble(1,1)-coord(:,1)).^2 (init_assemble(1,2)- coord(:,2)).^2 (init_assemble(1,3)- coord(:,3)).^2))./dr))==0);   
       init_assemble=round(rand(1,3),3);
    end
    assemble{length_assemble,1}=init_assemble;
    length_assemble=length_assemble 1;
end
coord_cell = arrayfun(@(x)ceshi(x,coord,dr),assemble,'UniformOutput',false);
coord_double=arrayfun(@(x)reshape([coord_cell{x,1}{:}],[],1), (1:n)', 'UniformOutput', false);
pre_coord_assemble=reshape([coord_double{:}],[],n);
logicjudge=arrayfun(@(x)ceshi2(x,addnumber,pre_coord_assemble),1:1:n);
%AA=arrayfun(@(x)ceshi2(x,A1,M),1:1:v);
[~,logice_coord]=find(logicjudge==1);
 if isempty(logice_coord)
     intcoord(2,:)=[];intcoord(end,:)=[];
 else
     intcoord=[coord; assemble{logice_coord(1),1}];
     [row,~]=size(intcoord)
 end
end
date_coordination=[date_coordination;[0 0 0;0 0 0];intcoord];
date_coord_length
end

（3）可是这个方法也存在一定问题，举例生成45个坐标后很难再生成第46个坐标，因为第46个坐标总是会超出A54的分布。经过仔细分析，过冷水发现还是之前生成的坐标有可能存在问题，于是过冷水就想出坐标轮换情况处理，假设第二个坐标生成有问题，把第二个坐标抽取，使得原来的i个原子数变成1-1个原子集，然后继续生成如果能够生成i 1个原子坐标就说明原先的2，i 1存在相互矛盾的情况，如果无法生成i 1个坐标就还是抽取现在的第二个坐标原先的第三个坐标，就这样反复优化，我们就能够优化出一组的合适的坐标使得其满足A54的分布。

addnumber=sort([Distance1;repmat(unique(Distance1),5,1)]);
date_coord_length=1;date_coordination=[];
intcoord=round(rand(1,3),3);
dr=0.002;
date_coord_length=1;date_coordination=[];
for date_coord_length=1:100
  row=1;  
while row<54
coord=intcoord;
AA=1; k=1;
while AA
   init_assemble=intcoord(1,:);
    while ~all(round((sqrt((init_assemble(1,1)-coord(:,1)).^2 (init_assemble(1,2)- coord(:,2)).^2 (init_assemble(1,3)- coord(:,3)).^2))./dr)<min(Distance1) ==0)|~all((max(Distance1)<round((sqrt((init_assemble(1,1)-coord(:,1)).^2 (init_assemble(1,2)- coord(:,2)).^2 (init_assemble(1,3)- coord(:,3)).^2))./dr))==0);   
       init_assemble=round(rand(1,3),3);
    end
    data1=[coord;init_assemble];
    [m,~]=size(data1);
    Distance11=arrayfun(@(x)(round((sqrt((data1(x,1)-data1([1:x-1,x 1:m],1)).^2 (data1(x,2)- data1([1:x-1,x 1:m],2)).^2 (data1(x,3)- data1([1:x-1,x 1:m],3)).^2))./dr)),[1:m]','UniformOutput',false);
    distance=reshape([Distance11{:}]',[],1);

    C=intersect(addnumber,distance);
    AA=~all(sum(addnumber==C')>=sum(distance==C'));%AA=all([sum(A1==C')>=sum(B==C'),ismember(B,C)']);
    k=k 1;
    if k>1000
        coord(1,:)=[];
        %coord(end,:)=[];
        k=1;
    end     
end
intcoord=[coord;init_assemble];
[row,~]=size(intcoord)
end
date_coordination=[date_coordination;[0 0 0;0 0 0];intcoord];
end

过程中使用到的子程序

function Distance11=ceshi(x,dataA,dr)
data1=[dataA;x{:}];
[m,~]=size(data1);
Distance11=arrayfun(@(x)(round((sqrt((data1(x,1)-data1([1:x-1,x 1:m],1)).^2 (data1(x,2)- data1([1:x-1,x 1:m],2)).^2 (data1(x,3)- data1([1:x-1,x 1:m],3)).^2))./dr)),[1:m]','UniformOutput',false);
end

function AA=ceshi2(x,A1,M)

B=M(:,x);
C=intersect(A1,B);
AA=all(sum(A1==C')>=sum(B==C'));%AA=all([sum(A1==C')>=sum(B==C'),ismember(B,C)']);
end

过冷水使用intcoord绘制生成的坐标数据对应的柱状图和Distance的柱状图做对比

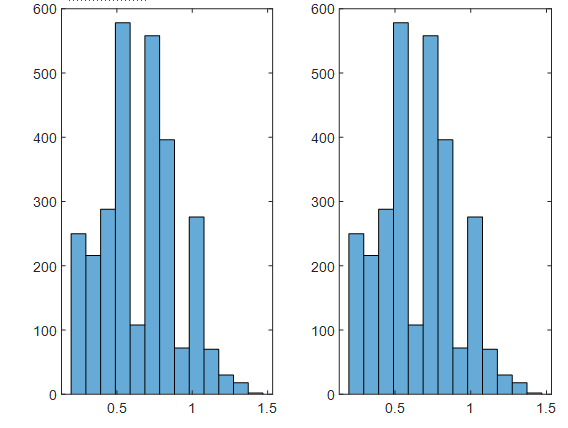
Distance_Monte_Carlo1=[];dr=0.002;Distance_Monte_Carlo=[];
for i=1:54
        dataj=intcoord;
        dataj(i,:)=[];
        distance =sqrt((data(i,1)-dataj(:,1)).^2 (data(i,2)-dataj(:,2)).^2 (data(i,3)-dataj(:,3)).^2);
        Distance_Monte_Carlo1=[Distance_Monte_Carlo1;round(distance/dr)];
        Distance_Monte_Carlo=[Distance_Monte_Carlo; distance ];
end
figure
subplot(1,2,1)
A=histogram(Distance,'BinWidth',0.098)
subplot(1,2,2)
b=histogram(Distance_Monte_Carlo,'BinWidth',0.098)

以上就是过冷水完美复刻已知分布这个问题就是Monte Carlo方法应用于动力学模拟的雏形，该问题合金并不是直接生成一个坐标分布，而是要生成一组坐标，分布只是判断坐标是否符合要求的条件，生成的坐标是有限制条件的，在限制条件下使得工作做起来比较难，当时解决问题可费事了，这是一个很好的Monte Carlo应用于复杂情况的案例，读者能够看懂应用于自己的实际需求中。

过冷水和你分享 matlab读取存储各种文件的方法文末有独家金曲分享