始于实验,陷于仿真,忠于流体
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐
来源:LBM与流体力学(ID:LBMCFD),作者:卢比与钢蛋。
实验和仿真就好像推动产品研发的两副车轮,他们时而相互扶持,时而相互鄙视,像极了一对相爱相杀的伙伴。不过有一位流体力学的大神却用自己的实际行动完美诠释了实验和仿真是可以手牵手,一起做朋友,那便是提出经典的k-epsilon 湍流模型的Brian Edward Launder 教授。
01 从实验流体力学开始
1939年,生于伦敦的Launder 很早便展示出自己的学霸属性。1961年,年仅22岁的他在伦敦帝国理工学院获得机械工程学士学位,并以全班第一名的身份获得Bramwell 奖章。随后,他进入麻省理工学院攻读硕士和博士学位,并以实验流体力学作为自己研究的起点。

Launde r在MIT 的燃气轮机实验室主要从事边界层实验工作,其主要的贡献是通过实验研究湍流边界层的加速效应。Launder 在1964年发表了经典的论文《Laminarization of the turbulent boundary layer in a severe acceleration》阐述了他的研究内容。简而言之,如果加速足够强,湍流边界层可以变成层流,从而大大减少传热速率,这种现象被称为层流化,对于涡轮的流动至关重要。
我们没有办法假设如果Launder一直在MIT从事实验流体力学的研究能够取得多大的成就,因为我们都知道结局是Launder成为了CFD的大师,人生或许就是如此:“努力决定能走多远,而选择决定行走的方向”——这一切的转折都来源于Launder博士毕业之后的选择。
02 又回到最初的起点
在MIT 完成博士学位后,Launder 于1964年回到帝国理工学院担任讲师,后来成为流体机械专业的教授,直到1976年去了加州大学戴维斯分校。Launder 在帝国理工学院供职12年,从25岁到37岁,他把最才华横溢的12年给了自己的母校。
在帝国理工学院,Launder 加入了当时已经功成名就的Brian Spalding 教授的团队,而就在同年,CFD行业的另外一位大佬Patankar 进入帝国理工学院,师从Spalding 教授攻读博士学位。

也许当时的人们很难想象,Spalding 的团队将在接下来的二十年收获一系列引领CFD行业的成就。作为现代CFD行业的创始人之一,Spalding 一直致力于CFD的工程化,其中很重要的一个研究方向就是为工业领域的流体仿真应用搭建合适的湍流模型,而Spalding 将这一重要的研究方向交给Lauder 来领导,于是便有了后来大名鼎鼎的k-epsilon 模型。
03 k-epsilon 模型的诞生
1924年,普朗特基于“混合长度理论”提出了CFD领域第一个实用的涡粘模型,封闭了雷诺平均的N-S方程的求解。作为湍流模型的起点,普朗特将混合长度定义为与到壁面的距离成正比,在今天看来当然不够严谨,他不仅忽略了边界层内的变化,也忽略了湍流本身的演化。
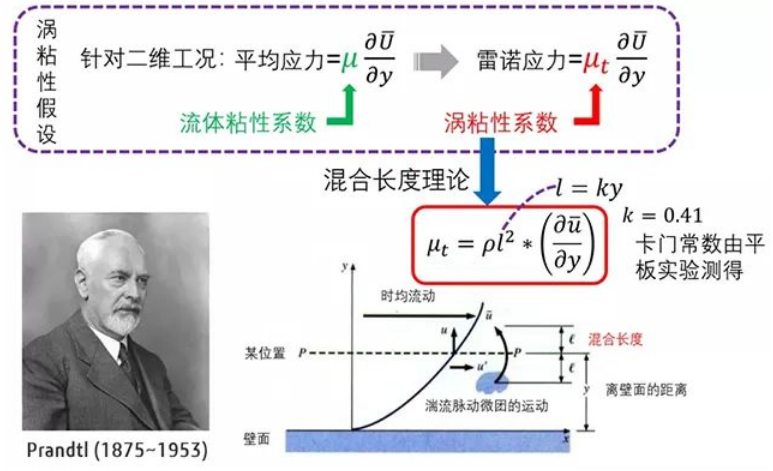
或许是得益于早年在MIT 做实验的经历,Launder 亲眼目睹过湍流的生成和耗散,尤其是流体在边界层附近的演化。另外,Launder 比普朗特幸运的是他站在更多的巨人肩膀上,尤其是1940年代,以柯尔莫果洛夫为首的统计学派为流体力学带来了全新的视野,让人们在湍流的无序中看到有序,为无规则的湍流制定了规则。于是,Launder 很敏锐的发现,如果用湍动能和耗散率来表示混合长度能够更准确的从物理层面上反映湍流的生成和耗散。
Launder 和他的博士生们从60年代后期到70年代开展了大量的工作。1972年,Launder 和他的博士生WP Jones 在论文《The prediction of laminarization with a two-equation model of turbulence》中提出了k-epsilon 模型,随后,他们又进行了一系列的测试,来校对湍流模型中的常数,最终在1974年Launder 和Spalding 共同署名的论文《The Numerical Computation of Turbulent Flows》中定义了我们今天所说的标准k-epsilon 模型,该文章自问世以来已经超过两万次的引用。

04 k-epsilon 模型的推导
正如前面所说的,k-epsilon 模型属于涡粘性模型,不过它变换了另外一种更加湍流的思想来求解混合长度,进而求解涡粘性系数:混合长度定义为流体微团耗散前所经过距离,因此,也可以定义为耗散时间和流体微团速度的乘积,当然流体微团的速度和脉动速度是相当的,通过经验系数来表示。于是,我们可以用湍动能和湍流耗散率来表示湍流粘性系数。
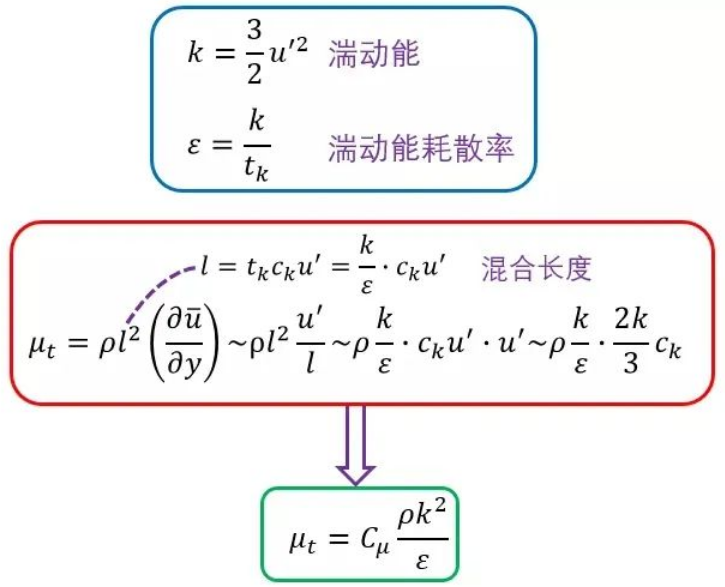
而面对多出来的两个未知量k 和epsilon,则需要补充两个微分方程来让方程的求解封闭。这便是我们熟悉的k 方程和epsilon 方程。不过需要特别指出的是补充的epsilon 方程中包含了经验系数,这些系数一般由实验得出,因此限制了k-epsilon 模型的适用范围。实际工程应用中,也有很多工程师会根据特定的应用场景修改相应的经验参数来匹配实验的结果。
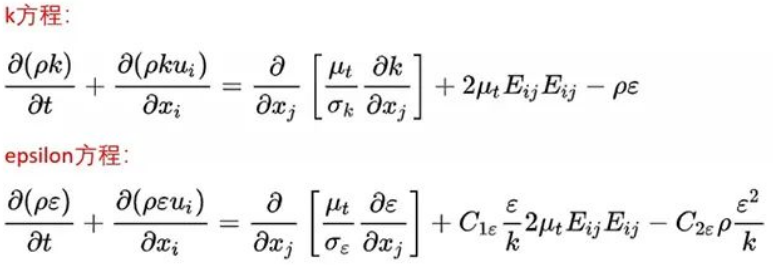
k-epsilon 模型本质上是在湍流各向同性假设基础上,对混合长度理论的进一步发展,因此相对于普朗特的模型,k-epsilon 模型适用于更复杂的流动。但是熟悉k-epsilon 模型的朋友都知道,它不适用于逆压梯度较高的流动,不适用于喷流和二次流。于是,Launder 在后续提出了一种更彻底的湍流模型。
05 最彻底的湍流模型
关于k-epsilon 模型不适用于逆压梯度较高的流动的问题,很多人从理论上推导,认为其原因是epsilon 方程中的经验系数来源于粘性底层中的阻尼函数,而阻尼函数的精度在强逆压梯度的流动中存在一定的问题,这样的说法当然没有问题,因此有很多人将精力花在了调校epsilon 方程中经验系数上面。可是事实证明,修改经验参数无法从根本上解决k-epsilon 模型的问题。
在实验流体力学中浸淫多年的Launder 敏锐的发现k-epsilon 模型的问题来源于其本质上为涡粘模型,因此,k-epsilon 模型同样假设雷诺应力与应变率成线性比例。然而,涡粘性假设在很多流动中被证明是不合理的近似,这才是k-epsilon 模型甚至是涡粘模型最大的问题。于是,Launder 和他的学生们一起提出了另一种更直观的湍流模型。1975年,Launder在流体力学的顶刊JFM(在此忍不住吐槽一下:大神发刊洪水漫灌,小民投稿举步维艰)上发表了一篇重要的文章《Progress in the development of a Reynolds-stress turbulence closure》。

文章提出了一种湍流模型,不再使用涡粘性假设,其中雷诺应力由这些变量的输运方程和湍流能量耗散率epsilon 的解来确定。模型特别注意压力和应变关系的近似;所采用的形式对壁面附近和自由剪切流中的应力进行了合理的分配。对于应变均匀剪切流和二维非均匀剪切流,包括射流、尾迹和尾流,新的湍流模型相对于k-epsilon 模型在求解精度方面有了明显的改善。此外,研究还表明,对于曲面上的流动,新的模型确实预测了二次应变项的强烈影响。这种方法称为雷诺应力输运模型或者更一般地称为二阶矩封闭。
二阶矩封闭的一个主要优点是,表示雷诺应力产生的项在它们各自的输运方程中精确地表示出来。当然,这些方程中的其他项必须是近似的,与两方程模型相比,现在有七个输运方程需要求解——需要更多的计算工作。当然,这种方法能够捕捉到比k-epsilon 模型更复杂的流动和现象。雷诺应力输运模型由Launder 和他的同事G. J. Reece 和W. Rodi 共同提出,因此也称为LRR 模型,很多人也将它称为最彻底的湍流模型。
06 辗转于高校与科研机构之间
1976年,Launder 离开帝国理工学院,来到美国加州大学戴维斯分校,担任机械工程系的教授。四年后,他又回到英国,加入了曼彻斯特大学理工学院成为热流体专业的负责人,一直工作了16年。年过60的Launder 辞去了曼彻斯特大学的职位,不过他依然活跃在流体力学和CFD研究的一线,在过去的20多年的时间里,Launder 在不同的科研机构担任重要的角色,比如2000-2006年,Launder 担任廷德尔气候变化研究中心的区域总监,随后他还作为英国皇家学会的成员,负责编写地球工程气候变化的声明。

虽然Launder 在近二十年的时间里并没有停下科研的脚步,不过相对于在帝国理工大学期间取得影响CFD发展的成就,Launder 后来的工作更多的是对之前工作的一些延续和总结,尤其是针对雷诺应力输运模型的延续。为了表彰Launder 对湍流建模的贡献,英国皇家学会和皇家工程院都将他选为Fellow。当然,他还获得了许多国际荣誉,包括很多大学的荣誉学位。
结语
作为CFD行业的先驱, Brian Launder 教授一直致力于湍流模型的开发,而由他提出来的k-epsilon 模型及其变种更是CFD走向工业化的基石。时至今日,各种商用CFD软件中,下拉湍流模型选项,k-epsilon 都是当之无愧的王者。
然而成名于CFD的Launder 却一直记得当年在MIT做实验的时光,也一直坚定的认为实验和仿真是相辅相成的,他无疑是“知行合一”的杰出践行者。最后就用Launder 的一段话作为总结吧:“我总是看到实验和建模并驾齐驱。虽然我关于建模的论文被引用最多,但实验无疑给了我洞察力,也为测试建模思想提供了数据基础。”




