大客车动力总成悬置系统解耦优化研究
1
动力总成悬置系统隔振效果的优劣,直接关乎到车辆的NVH性能,是乘座舒适性和耐久性的重要影响因素之一。己有学者对动力总成悬置系统的布置方案、支架设计、装配精度等方面做了较深入的研究。转矩轴理论和能量解耦分析法是目前悬置系统分析优化常用的两种方法。由于动力总成工作时,源至路面、发动机的激励力较为复杂,悬置系统不可能达到严格解耦,只能尽可能提升其能量解耦率。
悬置元件安装位置、安装角度与主轴方向刚度等参数,对悬置系统隔振性能影响较大,常作为悬置元件优化的设计变量。由于设计变量数目较多,尚没有特定的函数表达式描述各变量之间的关系,且对目标函数影响程度的大小难以分辨,导致悬置原件的设计与优化往往工作繁琐。处理该类
问题较快捷的方法是:先利用灵敏度分析法,有针对性地筛选变量,仅保留对目标函数影响较大的设计变量,再利用多目标优化算法计算设计变量的最优解。
常用三摆线法或者模态测试技术识别动力总成惯性参数,模态测试技术识别惯性参数操作方便,结果较为精确。根据测试参数建立系统简易六自由度振动模型。针对原始悬置元件隔振率偏低,隔振效果差的问题,采用NSGA-2算法对其主轴方向刚度进行左右悬置元件刚度不对称优化。能够增大最优解的可行域范围,不考虑左右悬置元件刚度对称的约束条件,更合理匹配悬置元件的刚度,对于优化悬置元件的隔振性能以及改善车辆的乘坐舒适性有很大的现实意义。
2 动力总成惯性参数的识别
以某客车动力总成为测试对象,通过柔性绳四点悬吊动
力总成模拟其自由悬挂的边界条件,布置ICP加速度传感器,利用LMS Test.Lab数据采集仪,锤击法测试振动加速度的频响函数信号。动力总成试验装置和坐标系位置如图1所示,频响函数曲线如图2所示。

图1动力总成试验模型
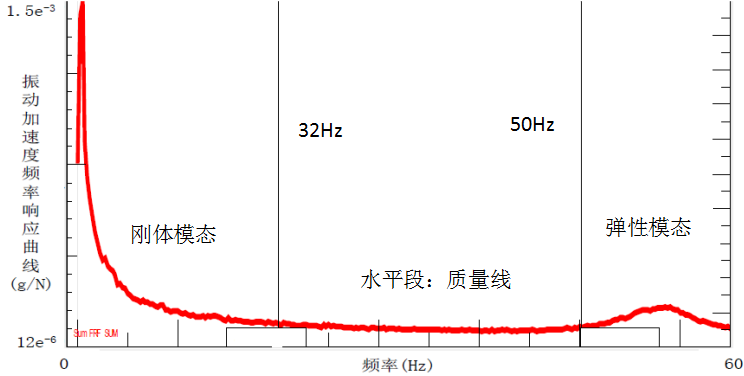
图2动力总成的频响曲线
质量线在约32-50Hz的水平线段,处于动力总成频响函数的刚体模态与弹性模态曲线之间,该线段仅由动力总成质量矩阵决定。在LMS Test.Lab的Rigid Mode模块中,输入动力总成质量m=1258kg,计算质心坐标为(0.837m,-0.061m,0.238m),转动惯量为Ixx=50.72kg.m2,Iyy=412.28kg.m2,Izz=372.75kg.m2。惯性积为Ixy=-6.34kg.m2,Ixz=-2.90kg.m2,Iyz=-20.18kg.m2。
3 动力总成悬置系统模型的建立
3.1数学模型的建立
建立六自由度简易振动系统模型,其惯性参数由模态测试得到,模型如图3所示。
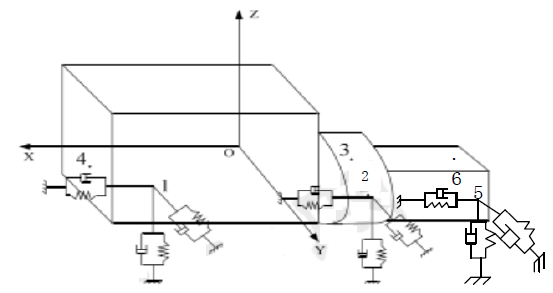
图3 六自由度简易振动模型
简易系统振动的一般表达式为:
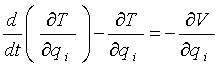
式中:T为振动系统的动能; V为振动系统的势能; qi为振动系统的广义坐标。
系统振动时,阻尼作用效果很小,忽略阻尼作用,系统自由振动方程为:
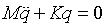
式中:q为广义坐标矢量
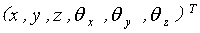
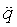

系统振动的动能分为两部分:一是沿质心平动的动能,二是绕质心转动的动能。即:
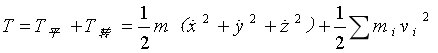
式中:m为动力总成的质量; vi为系统的某个微小质量相对于质心运动的速度。
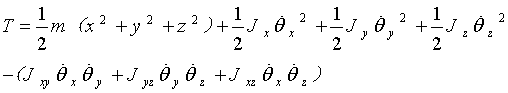
写为矩阵形式,系统的总动能的表达式为:
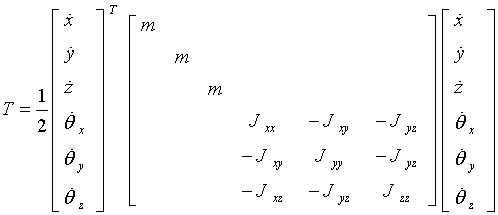
求解的质量矩阵为:
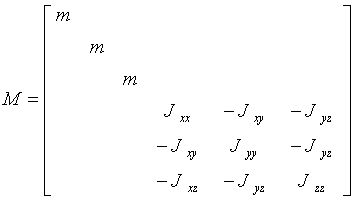
刚度矩阵K的计算较为繁琐,详细的推导过程,可参考《汽车工程手册》基础篇P313。
固有频率与解耦率的计算由式(2)可知:
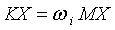
在第n个广义坐标上,振动能量为:
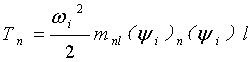
式中:
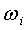

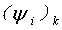
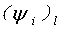
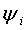
第n个广义坐标上,振动能量分配的百分比为:
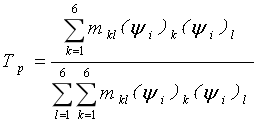
能量解耦法优势在于不受动力总成的类型、悬置元件的个数、安装位置等条件的限制,具有普遍适用性。
3.2 动力学模型建立
动力总成悬置系统简化原则:
(1)将动力总成以及车身看作是刚体;
(2)不考虑悬置元件的扭转刚度以及阻尼;
(3)不考虑动力总成工作时的不正常波动。
原始方案悬置元件的坐标位置如表1所示、主轴静刚度(左右对称位置刚度值相同)如表2所示。
表1 悬置元件坐标位置 表2 悬置元件的静刚度
悬置元件采用多体动力学软件Adams中的Bushing(衬套)模拟,能够合理的表达出各个方向的受力情况。忽略阻尼作用,将Bushing扭转刚度设置为零,仅考虑主轴方向刚度,表达悬置元件的力学性能,建立动力学模型如图4所示。
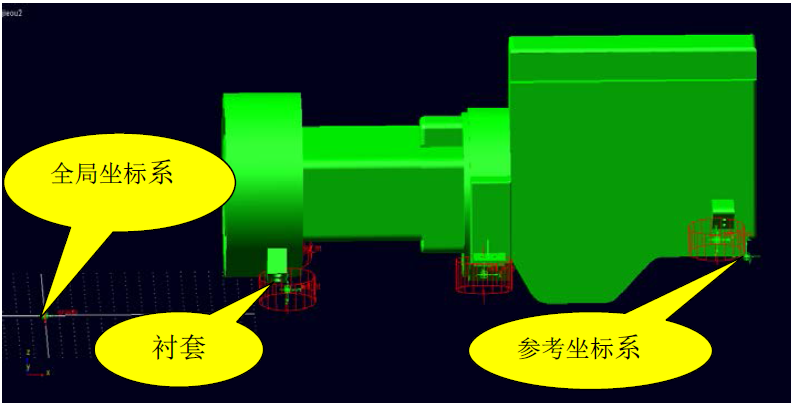
图4 Adams动力学模型
动力学模型的正确性对其固有频率、解耦率的计算,以及下文悬置元件刚度的优化非常重要,从两个角度进行验证:
(1)各悬置元件垂向支反力
运用静平衡分析法,在Adams中测试所建模型各悬置点垂向支反力总和为12328.4N,而动力总成质量m=1258kg。支反力与动力总成的重力基本一致,证明所建模型各构件的拓扑关系正确。
(2)动力总成的固有频率
表3 Matlab与Adams计算固有频率结果对比
3.3 解耦率的计算
Adams软件的Vibration模块,一般用于振动系统的固有频率、模态振型的分析计算,以及某一振动阶次不同方向的振动能量占能比的计算。对于原始悬置元件,动力学仿真计算振动能量的分布结果如表4所示。
表4原始悬置元件振动能量分布
由表4可知,原始悬置系统有较严重的耦合现象,Z、RZZ方向在第3、4阶固有频率处振动能量耦合度较大,X、RYY方向解耦率分别为61.58%、68.82%,远低于工程上能够接受的80%的标准,但Y、RXX方向的解耦率均超过了90%,是较为理想的解耦状态。
4 动力总成悬置系统的优化与设计
对于设计变量个数为n个,目标函数为m个,约束条件为a+b个的多目标优化问题,其数学表达式可写为:

其中,
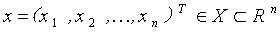
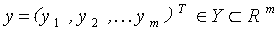
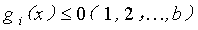
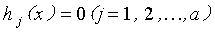
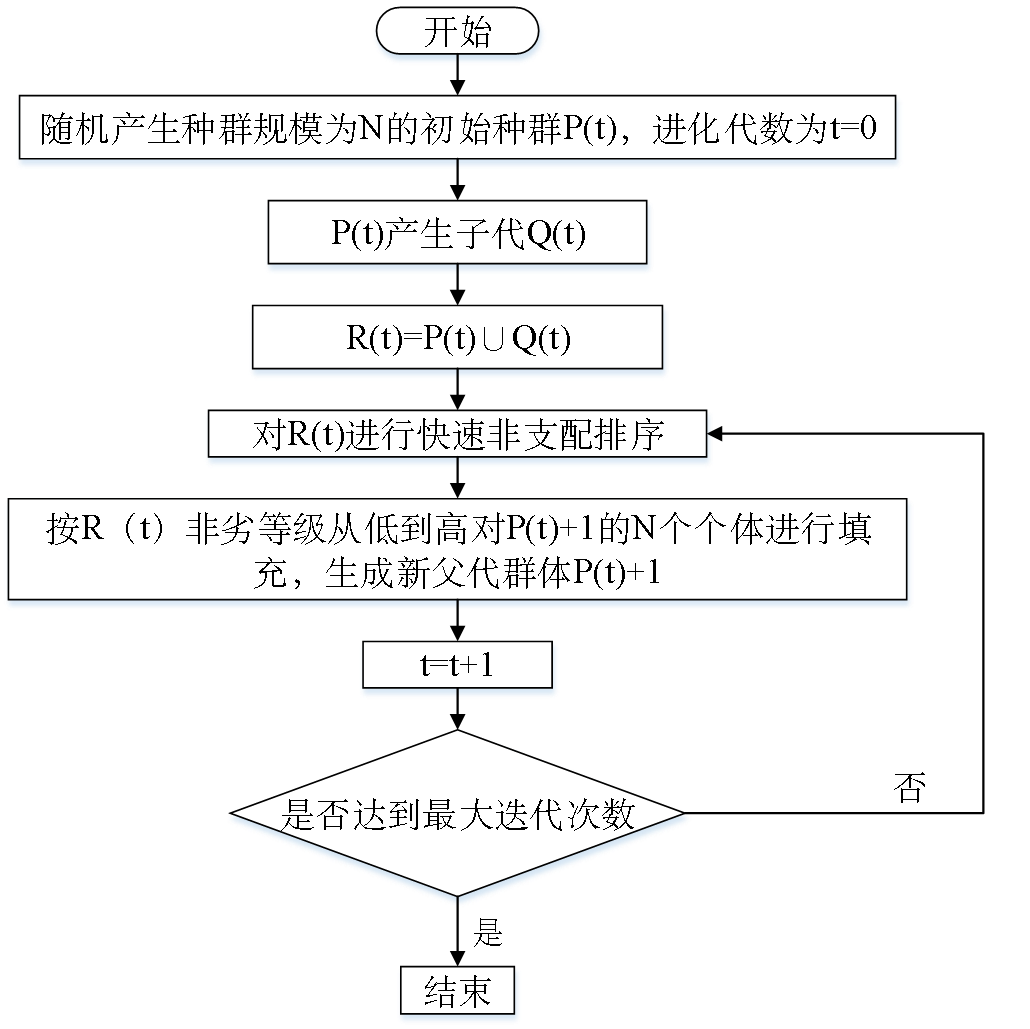
图5 NSGA-2算法的主流程图
本次优化过程的参数设置:种群规模200,代数80,交叉率为0.9,变异率为0.1,交叉分布指数为10,突变分布指数为20。原始悬置元件各向刚度范围如表5所示。
表5悬置元件刚度值的范围
应企业生产方案的需求,选取六个悬置元件的主轴三向刚度作为设计变量,Z向振动频率在5-12Hz为约束条件,6个方向解耦率均达到最大化为目标函数。采用NSGA-2算法对悬置元件左右侧刚度进行不对称优化。经灵敏度分析,仅保留对目标函数影响较大设计变量:左前悬置Kx、Ky、左中悬置Kx、左后悬置Ky、Kz、右前悬置Kx、Ky、右中悬置Kx、Ky、右后悬置Kz。六个悬置元件的18个主轴刚度变量缩减为10个。将Isight与Matlab无缝集成后,对10个设计变量进行多目标优化。优化后的刚度结果如表6所示。
表6 悬置元件优化后的刚度
将表6的计算结果赋予Adams中的Bushing,重新设置悬置元件的主轴刚度。仿真计算优化后的动力学模型的固有频率和振动能量解耦率。固有特性优化结果如表7所示。
表7固有特性优化结果
与原始悬置元件相比,NSGA-2优化算法在满足各方向能量解耦率最大化的条件下,重新匹配悬置元件的主轴刚度。能量解耦率都达到了90%,消除了振动耦合严重的现象。且Z方向的固有频率为9.21Hz,满足约束条件的要求。















.jpg?imageView2/2/h/336)
