基于CFD两相流的混合效果计算研究
本文摘要(由AI生成):
本文主要介绍了一种基于CFD的方法来验证混合器的混合效果。通过使用Ansys Workbench Cfx软件进行计算,包括几何模型处理、网格划分、求解设置、求解和结果提取等步骤。在求解设置中,采用SST湍流模型、标准壁面函数和体积分数云图等方法。计算结果显示,有混合模块的工况下,流体介质1和2的体积分数在整个横截面上比较均匀,混合效果较好。
1.计算目的
为了衡量某混合器的混合效果,本文采用基于CFD的方法对某混合装置的混合效果进行了验证。
2.计算方法
具体的完成这一工作则是通过商用流体计算软件Ansys Workbench Cfx 来完成的,其基本计算流程包括几何模型处理,网格划分,求解设置,求解,结果提取等几个步骤。
通过三维建模软件UG进行几何模型的绘制,并将其导入workbench求解模块的几何中,采用非结构网格进行划分,并在混合模块处进行必要的网格加密。
3.物性输入
物体1:
粘度:500Pa*s;
密度:0.45kg/l=450kg/m^3
速度:7kg/hr;
物体2:
粘度:0.01Pa*s;
密度:0.5kg/l= 500kg/m^3
速度:0.15kg/hr;
这些参数可以在CFX中插入新物质。
这里需要注意的是,由于该计算更多关注流动问题,因此只需要设定液体的密度和粘度,而不需要设定其他参数。
4.求解设置
在求解设置中,通过在求解区域设定两种材料,不考虑传热效果,湍流模型采用SST模型,标准壁面函数,对于两种流体间,考虑两者之间的各种分子间相互作用力。在进口中心处给定体积分数为1的流体介质2(纯流体介质2),而其他部分则给定体积分数为1的流体介质1(纯流体介质1),两者质量流量满足97:3的要求。为了便于计算收敛,模型进出口进行了适当延长。计算采用稳态求解器,即不考虑时间因素对计算结果的影响。
采用稳态求解方式。同时为了说明混合效果,进行对比研究,即对存在混合模块和不存在混合模块两种工况进行对比计算研究。
5.计算结果
在后处理中,由于重点关注的是混合效果。因此,对两种物质的体积分数(Volume fraction)进行提取。具体提取的是圆管中心截面处和模型进出口的Fluid1和Fluid2的体积分数云图。如下图所示。
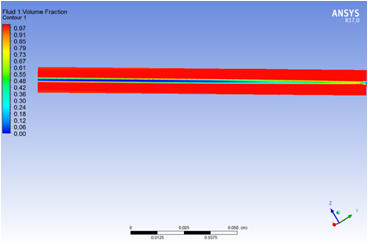
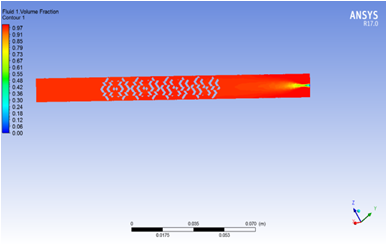
(a)无混合模块 (b)有混合模块
图1 有无混合模块的流体介质1在管道中间截面体积分数
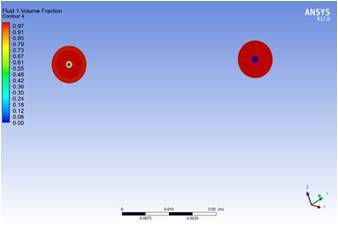
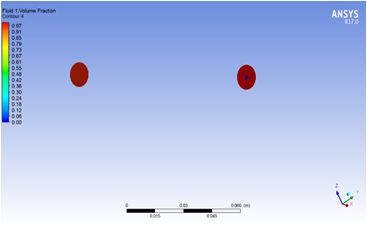
(a)无混合模块 (b)有混合模块
图2 有无混合模块的流体介质1在管道进出口截面体积分数
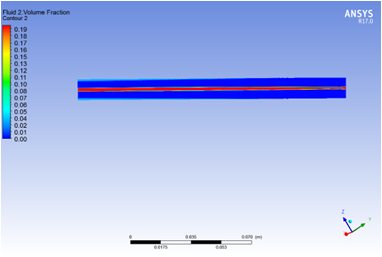
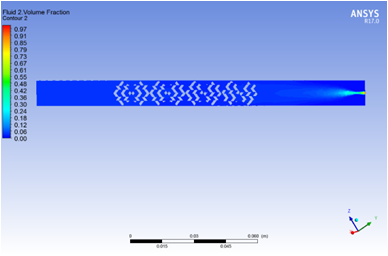
(a)无混合模块 (b)有混合模块
图3 有无混合模块的流体介质2在管道中间截面体积分数
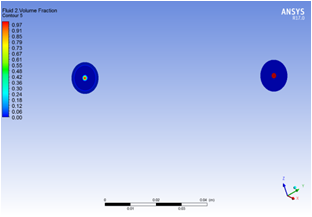
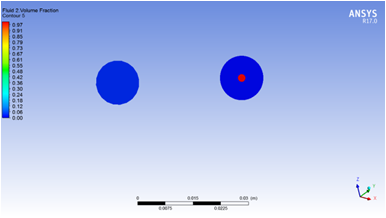
(a)无混合模块 (b)有混合模块
图4 有无混合模块的流体介质2在管道进出口截面体积分数
从图1可以看出,无混合模块的中截面,流体介质1的体积分数在管道两侧较高,而在管道中间较小,基本保持了进口处体积分数趋势,两种流体混合效果较差。而对有混合模块的情况,由于混合模块对流体的阻挡作用,在流体遇到混合模块之前两者就已经进行了混合,即流体没有通畅的通过管道,而在混合模块之前出现了“拥堵”现象,流体介质流动轨迹发生了变化,这种现象有助于两种流体的混合,可以看出,在该种情况下,管道出口流体介质1的体积分数在整个横截面上比较均匀。这从图2也可以看出,即进口截面,中心处流体1的体积分数为0,而周围为1;在出口处,无混合模块的管道,仅仅在中心区域发生了某些微小的混合,而有混合模块情况,出口整个截面体积分数都比较高,接近1.
图3和图4是针对流体介质2的情况,可以看出其体积分数的云图与图1和2中云图的趋势刚好相反,这是因为两种流体介质的体积分数满足相加为1的条件。
如果采用定量的方式对结果进行分析,即提取流体介质1在管道中心线上体积分数变化情况。可得到如下曲线图。

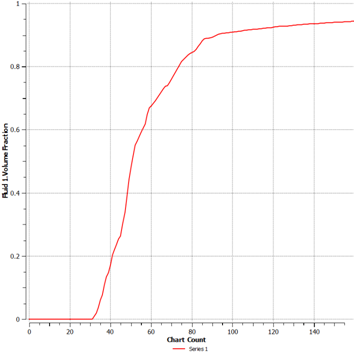
(a)无混合模块 (b)有混合模块
图5 有无混合模块的流体介质1在管道中心线上体积分数变化示意图
图5展示了流体介质1在管道中心线上体积分数变化情况,从图可以看出,对于无混合模块的工况,其体积分数始终保持在较低的水平,而对于有混合模块的情况,在管道入口处流体介质1的体积分数保持了较低的水平,但是随着混合流体接近混合模块,其体积分数逐渐上升,在管道出口,体积分数可达到90%以上,从而达到了很好的混合效果。
6.总结归纳
在两相流的实际计算中,需要设定的是在两相公路传递过程中的拽力(Drag Froce)模型及拽力系数,这个参数应该通过实际试验获得,但是由于试验条件的限制,该参数无法详细获得,因此,从定量上数据讲,该参数无法获得。但是定性分析却是可能保证的。这也是目前获得CFD计算精确的障碍。