信号完整性DOE设计之100G以太网优化
上篇文章介绍了DOE在DDR仿真中的应用,对于高速Serdes,同样的方法可以优化链路设计。 本文演示DOE 和 RSM 在 CEI 28G VSR 设计中的应用。展示从创建 DOE、将数据拟合到模型、确定拟合优度和可靠性,以及使用模型进行“what-if”分析、优化设计因素并量化制造偏差影响的流程。
01
—
DOE分析方法
任何类型分析中最重要的一步是确定工作目标。阿尔伯特·爱因斯坦曾说过:“如果我只有一个小时来拯救世界,我会花五十五分钟思考问题,只花五分钟思考解决方案。” 同样,在开始实际使用 DOE/RSM 方法进行工作之前,明确定义待解决的问题以及答案的 准确度至关重要。
DOE 和 RSM 流程图强调了分析的迭代性,因为它允许在流程的每个步骤中不断完善假设。此外,如果缺乏明确的分析目标和退出标准,这种方法可能会导致浪费周末时间,并导致无休止的审核。
用统计学思维应用在信号完整性,即在存在不确定性的情况下做出决策,对某些人来说可能不太舒服。DOE/RSM 分析并非依赖于完全确定的分析,而是提供介于置信区间之间的答案,从而表明结果的准确性。完全确定和统计学思维之间的唯一区别在于:前者会假装消除任何不确定性,而后者会量化、仔细审查并传达不确定性。不确定性总是存在的,最好的方法是理解它、减少它并拥抱它。坦然面对不确定性。
建模的目标是通过对因子空间(由 DOE 表提供)进行采样,然后用多项式方程拟合数据来表征真实响应。从这个意义上讲,模型实际上是最能拟合数据的方程。
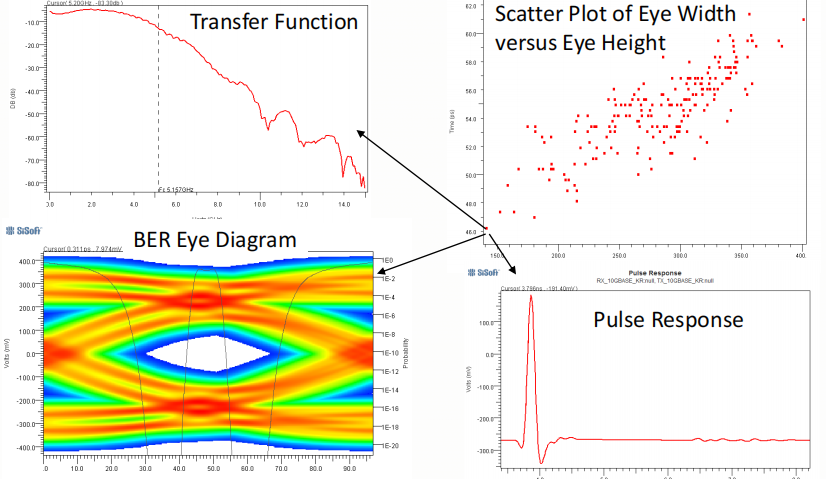
下图 显示了模型的一个直观示例,其中给出了链路的眼高与走线长度和阻抗的关系。请注意,该模型仅仅是实际响应的近似值,只有在准确的情况下才能代表现实。此外,从表面曲率可以看出,该模型是一个二维抛物线,与数据拟合度最高。模型形式和通过普通最小二乘拟合获得的系数估计值如下式 (1) 所示:
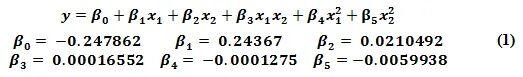
虽然这个表面代表了模型与数据的最佳拟合,但它并没有回答这个问题:这是代表“真实响应”的最佳模型吗?在这种情况下,为长度因子添加更高阶的多项式项可能会更好地捕捉迹线的谐振行为。虽然找到绝对最佳的模型可能是一个难以实现的目标,但我们当然可以通过逐步改进模型形式来实现。“过于简单”的模型会导致重要的响应特性被平滑处理,而“过于复杂”的模型则可能导致过分强调某些响应特性,而忽略其他更重要的响应特性。
人们可能认为,要找到最佳模型形式,只需将大量多项式项应用于模型拟合,看看哪些项是显著的。这种方法的困难在于,可用于拟合的模型形式受到响应采样的限制。如果沿因子维度只有两个数据样本,则最多可以用一条直线拟合数据。如果有三个数据点,则最多可以拟合一条二次线,进一步,如果最多有四个数据点,则可以拟合一个三阶多项式。因此,在某个时候,给定一个固定的采样集,可用于拟合的模型是有限的。这些限制导致人们认为因子空间的采样也必须考虑模型形式,以便模型拟合可以准确地估计真实响应。
从概念上讲,使用连续因子可以迭代直至获得理想的采样和模型形式,从而实现高质量的模型拟合。然而,在实践中,互连的各个部分通常由可能仅包含离散层级的块表示,例如以 S 参数模型为特征的连接器系列。在这种情况下,采样的分辨率是固定的,高阶系统响应特性会与低阶系统响应特性混叠,从而限制了分析。
模型假设的最后一个方面是多项式能够充分描述响应面。还有其他数学上更复杂的模型,例如高斯过程模型,它具有一些令人惊讶的特性(例如零残差和空间认知插值)。DOE/RSM 方法的绝大多数信号完整性应用都可以用多项式模型充分描述。
将模型拟合到数据的过程通常采用普通最小二乘 (OLS) 回归分析。该估计方法假设输入因子不相关,拟合误差方差在不同因子或因子水平之间保持不变,且残差误差呈正态分布。这些假设可以根据需要放宽,但需要更复杂的最小二乘法,例如广义线性模型(允许正态分布以外的其他残差误差分布)和广义最小二乘法(允许相关因子和非均匀误差方差)。
02
—
28G VSR系统分析
CEI 28G VSR设计挑战:
1、更加的复杂系统设计
——如何管理相互冲突的目标?
2、需要检查数百万种系统配置。分析迭代时间
——得出答案需要多长时间?如果模拟过程耗时几分钟,而有数百万个设置需3要检查,那么整个模拟过程可能需要几个月的时间!
3、设计决策——如何处理多个设计决策?
4、制造变化——这将如何影响性能?我的设计能否最小化风险?
链路定义: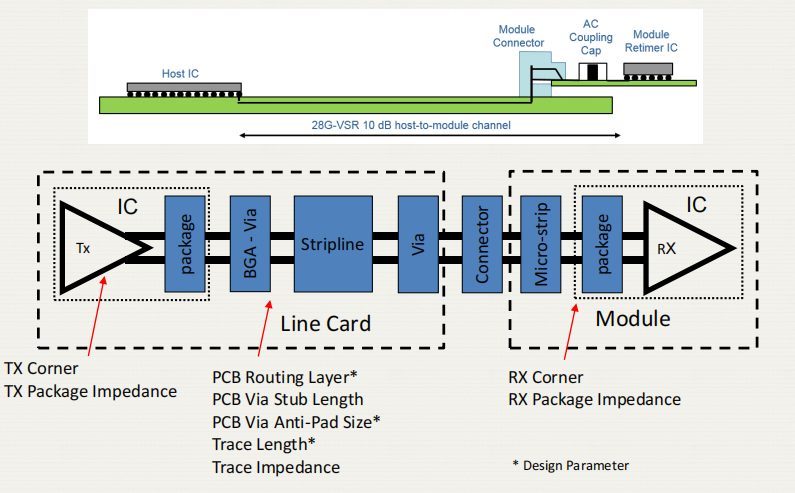
问题?
线路卡的最大允许跟踪长度是多少?
定义参数空间: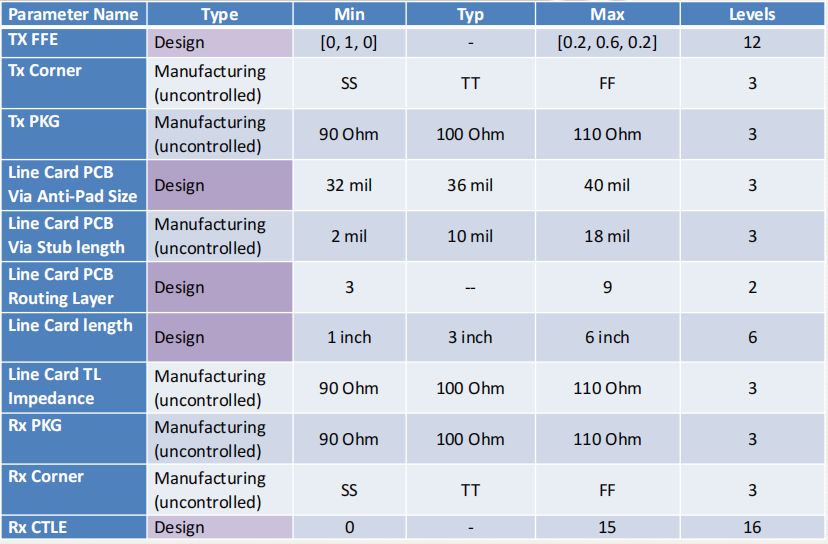
03
—
DOE设计
实验设计是一种允许在最小化运行次数的同时对空间进行良好覆盖的方法。
包括:精确抽样、随机抽样(蒙特卡罗)、逐个因素抽样等
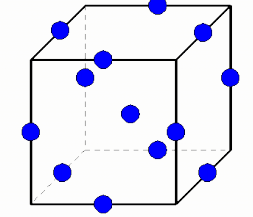
系统响应:可以采用多种评价方式,这里采用EH和EH。
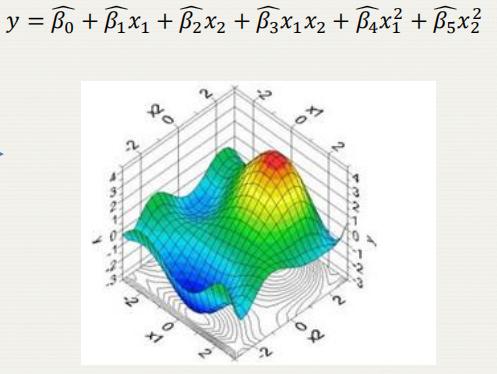
RSM: Response Surface 响应面方程描述了解释变量(x)与响应(y)之间的关系。

通过系数β的估计值,我们得到了一个能够近似描述响应特性的方程。该方程可表示为:
响应曲面在多大程度上代表真实响应?
我们有N个数据点,可以用来测试方程。真实响应与预测响应之间的差异称为残差。
•根均方误差(RMSE)是一个衡量残差的单一数值指标。
•响应解释数据变异的能力如何?
•R²表示模型能够解释的数据变异比例。[0,1]
•R²adj是一个类似的度量,但会因为引入额外的模型项而进行惩罚。
R 2和 R 2调整之间巨大差异表明模型中存在不必要的项。
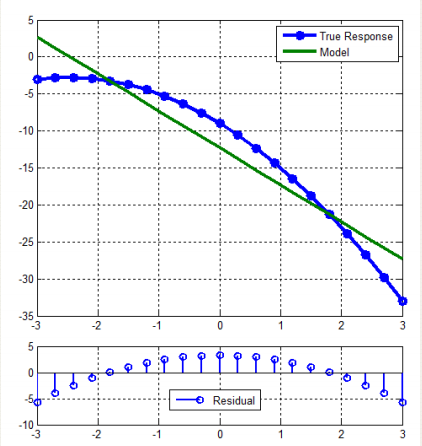
残差应呈正态分布:
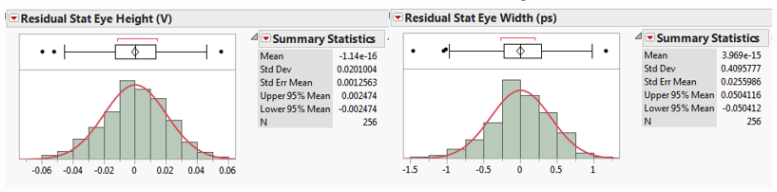
残留物应无结构:
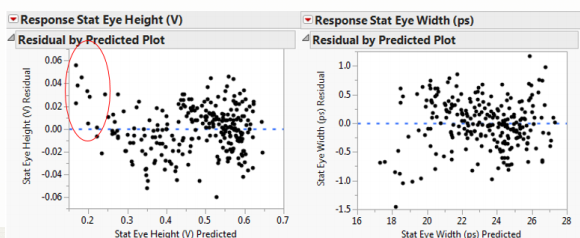
28G VSR设计示例:
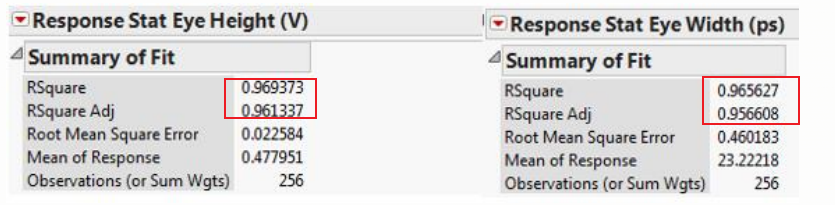
这似乎是一个很好的匹配,但最终的测试是使用模型进行预测,然后模拟预测条件以验证预测。
04
—
探索和优化
一旦所有步骤都确保了模型拟合的合理性,并确信其中的不确定性已经大致了解,我们就可以探索模型所代表的因子空间。在本应用中,可视化一个 10 维空间是一项艰巨的任务,幸运的是,有一些工具可以简化此类分析。一种称为预测刻画器的图表,显示了在所有其他因子保持不变的情况下,每个因子的响应情况。这种类型的图表在交互式使用时最为有用,但从下面使用的静态视图中也可以获取更多信息。 例如,请考虑图 10 所示的双因子 RSM 拟合的预测刻画器图表。
•应使用哪个PCB层进行高速布线?
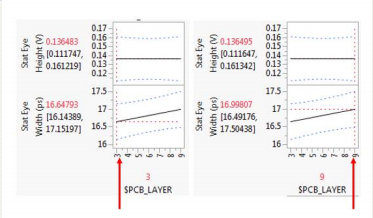
该预测分析器图显示了不同解释因子(走线长度 (PCB_LEN) 和走线阻抗 (PCB_Z))的眼高响应。由于走线长度因子的斜率最大,因此我们可以说它是因子空间中此区域中最具影响力的因子。如果这些因子之间存在任何相互作用,则该线的有效斜率可能会在因子空间的其他区域发生变化。此外,该图表明,当 PCB_LEN=3.5 且 PCB_Z = 100 时,预测眼高为 0.538 V,95% 置信区间为 [0.514, 0.562] V,这相当于声明预测眼高在 95% 置信区间内为 0.538 +/- 0.0234 V。在预测分析器图中,置信区间用围绕实线黑色预测响应的蓝色虚线表示。
•最佳的过孔反焊盘尺寸是多少?
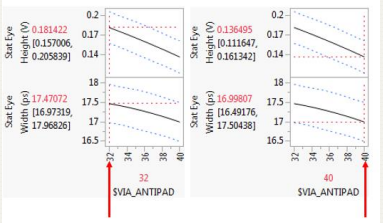
制造变更:将分布分配给制造因素
下图中阻抗等都服从某种分布
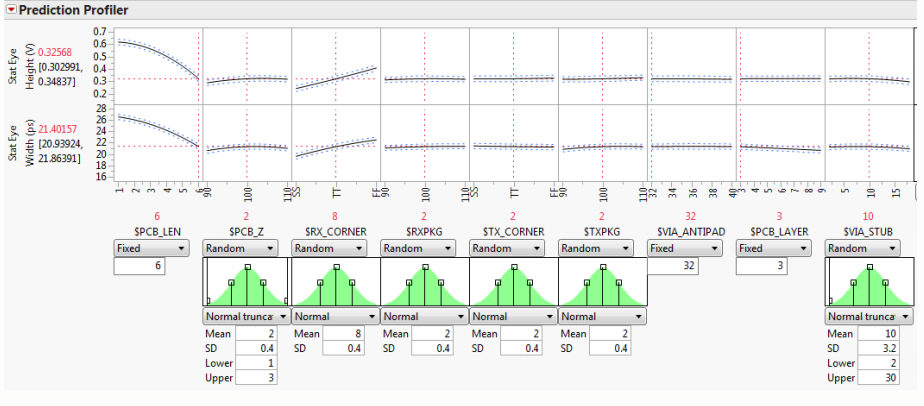
随机生成100万个系统条件,并利用拟合方程量化性能:
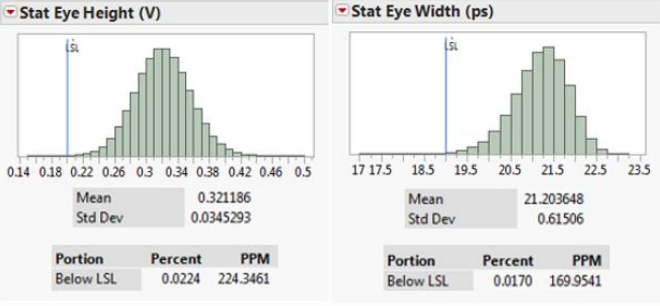
本文展示了助力首个CMOS 28G VSR/100G以太网PHY设计的方法。解决了接口设计问题:在PCB的哪一层进行布线、使用多大尺寸的过孔反焊盘以及允许的最大走线长度。我们识别了最坏情况,并量化了制造偏差对性能的影响。所有这些都是通过DOE/RSM方法完成的。DOE无需耗费数月计算时间模拟数百万种条件,而是仅用256次运行即可智能地对因子空间进行采样。最小二乘模型拟合找到了与数据最佳拟合的响应曲面,并在模型验证后用于预测整个因子空间的系统性能。必须强调的是,随着模型假设的变化,该方法需要进行多次迭代。总体而言,DOE/RSM 方法已被证明是一种理解和优化令人眼花缭乱的大型因子空间的强大方法。
参考:
1、Richard Allred 、Barry Katz 、、Ish Hosagrahar、Chao Xu、Wiley Gillmor;How Design of Experiments Saved My CEI 28G VSR Design
end
本文内容仅代表作者观点,如有侵权,请联系删除。





