GISSMO 韧性断裂准则的标定
GISSMO 韧性断裂准则与工程中常用的 Johnson-Cook 断裂模型的不同点在于,该模型考虑了材料从受损、非线性损伤累积到材料断裂失效的全过程,并且能预测材料在不同应力状态下的失效行为,适于分析与预测金属板材碰撞与成形过程中的断裂问题。
一、GISSMO 韧性断裂准则简介
GISSMO 韧性断裂准则主要使用非线性损伤累积方式定义材料的失效行为,如下式所示。在唯象断裂模型中,通常定义不与本构模型耦合的外部变量 D 来描述材料的损伤行为。当仿真中单元的 D 值达到 1 时,在仿真中就会被删除。
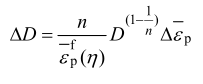
式中: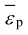 为等效塑性应变;
为等效塑性应变;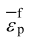 为材料发生断裂时的等效塑性应变,其数值与应力状态相关;n 为损伤系数。
为材料发生断裂时的等效塑性应变,其数值与应力状态相关;n 为损伤系数。
GISSMO 模型除了能够表征不同应力状态下材料的断裂行为,还将韧性断裂中材料的失稳现象也考虑其中。材料的软化行为由变量 F 定义,如下式所示:
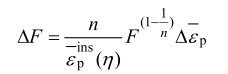
式中: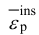 为不同应力状态下的等效失稳塑性应变。当单元的 F 值达到 1 时,其应力会发生软化现象,软化后的单元应力由下式计算得到。
为不同应力状态下的等效失稳塑性应变。当单元的 F 值达到 1 时,其应力会发生软化现象,软化后的单元应力由下式计算得到。
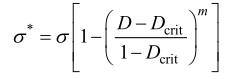
式中:σ*为发生软化后的应力;σ 为软化前应力;Dcrit 为 F=1 时变量 D 的临界值;m 为衰减系数。
二、GISSMO 韧性断裂准则参数确定
由GISSMO 韧性断裂准则简介可知,需要输入模型中的参数有等效断裂塑性应变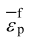 、等效失稳塑性应变
、等效失稳塑性应变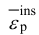 、衰减系数 m 及损伤系数 n。对于等效断裂塑性应变来说,通常提取断裂前一帧的应变数值作为等效断裂塑性应变。但对局部变形较大的简单剪切和拉伸剪切实验来说,变形后期试样表面的云图破裂导致无法得到断裂前的最大应变值,且剪切变形并不会出现韧性断裂模式中的剪切软化现象,其失稳等效塑性应变通常设置为较大值而不需要求解。对其他模型中的等效失稳塑性应变
、衰减系数 m 及损伤系数 n。对于等效断裂塑性应变来说,通常提取断裂前一帧的应变数值作为等效断裂塑性应变。但对局部变形较大的简单剪切和拉伸剪切实验来说,变形后期试样表面的云图破裂导致无法得到断裂前的最大应变值,且剪切变形并不会出现韧性断裂模式中的剪切软化现象,其失稳等效塑性应变通常设置为较大值而不需要求解。对其他模型中的等效失稳塑性应变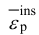 、衰减系数 m 及损伤系数 n 来说,实验中无法准确测得上述参数值。因此,常采用实验-有限元混合方法反求模型参数。文中采用 LS-OPT 软件对 6016 铝合金 GISSMO模型参数进行反求,输出仿真载荷-位移曲线与实验进行对比,反求流程如图所示。
、衰减系数 m 及损伤系数 n 来说,实验中无法准确测得上述参数值。因此,常采用实验-有限元混合方法反求模型参数。文中采用 LS-OPT 软件对 6016 铝合金 GISSMO模型参数进行反求,输出仿真载荷-位移曲线与实验进行对比,反求流程如图所示。
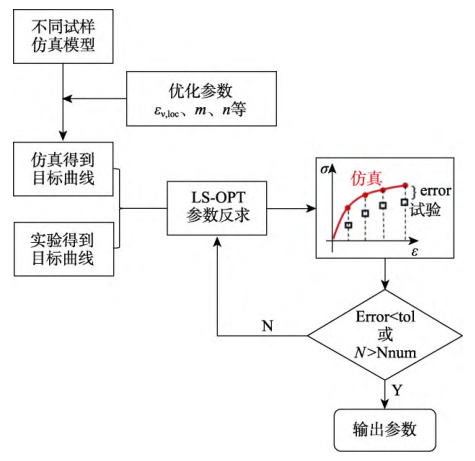
图1 LS-OPT 参数反求流程
在对 6016 铝合金进行参数反求的过程中,考虑到材料的各向异性,为提高仿真精度,选择 LS_DYNA材料库中的 MAT_36_3-PARAMETER_BARLAT_NLP材料模型,输入 0°、45°、90°这 3 个方向上外推后的真实应力-应变曲线。为了保证仿真精度,目标区域网格大小划分为 0.5 mm。
三、有限元仿真与实验结果对比
经 LS-OPT 软件优化后的 GISSMO 断裂模型参数如表 1 所示,对应得到的断裂及失稳曲线如图2所示。
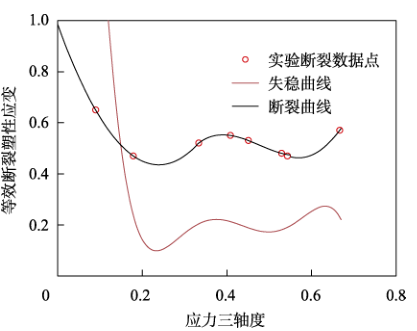
图 2 输入 GISSMO 模型的 6016 铝合金断裂及失稳曲线
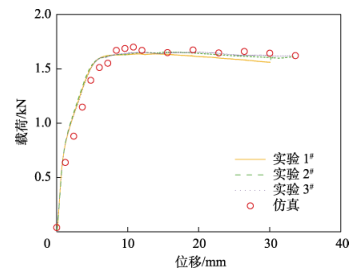
图 3为使用优化后的 6016 铝合金 GISSMO 韧性断裂模型参数进行实验后,各组实验与仿真的载荷-位移曲线对比,仿真峰值力数值与断裂位移数据均与实验结果相吻合,且仿真断裂位移误差与实验值的误差均小于 5%,满足工程使用要求,验证了 6016 铝合金GISSMO 模型的有效性。
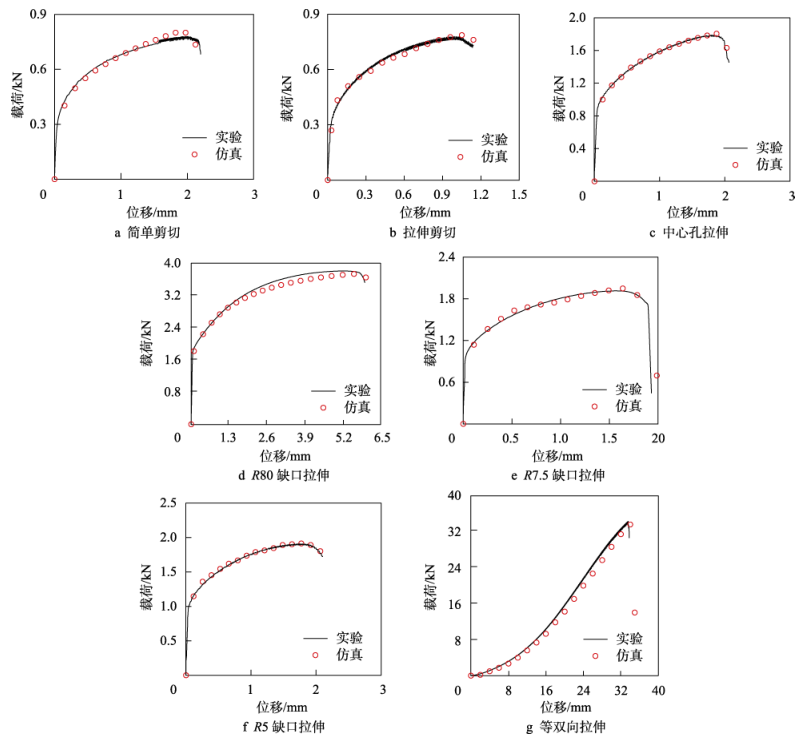
图 3 试样仿真与实验载荷-位移曲线结果
四、网格正则化过程
网格划分情况同样会影响有限元仿真的结果,在整车碰撞与汽车零件成形仿真中,为了兼顾仿真准确性与仿真效率,GISSMO 韧性断裂准则通过引入网格依赖性因子来考虑尺寸效应的影响,使同一应力状态、不同网格尺寸的仿真结果相同。
为了校准不同网格尺寸下的网格依赖性因子值,建立了 0.5、1、2.5、5、10 mm 网格尺寸的单向拉伸实验仿真模型。在未对不同网格大小的仿真模型进行归一化处理前,仿真结果如图所示,试样断裂位移随网格尺寸的增加而加大,导致仿真累积误差增加。
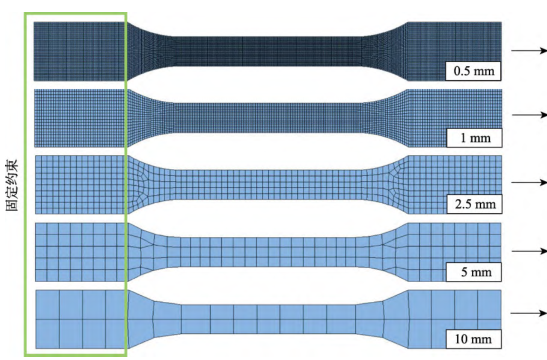
图 4 不同网格大小的单向拉伸仿真模型
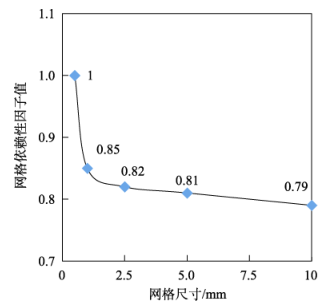
图5 网格依赖性(正则化)因子曲线
通过参数反求的方式获取相应的因子值,使不同网格尺寸的模型均能得到与实验一致的载荷-位移曲线,如图所示。
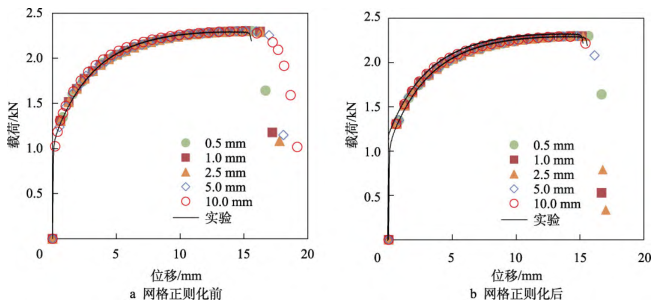
图6 不同网格尺寸下单向拉伸工况载荷-位移曲线