电磁矢量有限元迭代神器：FGMRES+AMS

3天前浏览11

介绍

对于研究三维电磁矢量有限元仿真朋友应该了解，矢量有限元得到的稀疏矩阵条件数很差，这导致使用传统的迭代求解器很难收敛到足够精度。因此，基于辅助空间预条件（AMS）的FGMRES迭代求解器孕育而生，专门针对maxwell方程的迭代求解器。很多文献已经证明，对于大规模自由度矩阵而言，这种迭代求解器是稳定的，计算收敛性好，占用内存空间远小等优点。

本文是从开源代码中把这部分提取出来，简化接口，测试效果，降低该方法的使用门槛。

一、原理简介

FGMRES 之所以称为“灵活”广义最小残差法，是因为它在迭代过程中允许动态更换预条件子；而 AMS（Auxiliary-space Maxwell Solver）正是针对 Maxwell 方程体系专门构造的一类代数预条件子，可与 FGMRES 无缝配合

对于上述FGMRES迭代求解器流程而言，其中

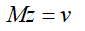
这里M即是预处理矩阵，根据这个系统，构造一种基于物理或者原方程特征的预条件矩阵，使得该矩阵足够逼近原始矩阵的同时，又能高效求解。进一步说明，则是预处理矩阵M的逆与原矩阵相乘得到的系统矩阵的条件数足够的小，这就能保证预处理后的线性系统能够很容易迭代收敛。

具体处理方式：首先对于Maxwell方程而言，都可以获得复数形式的方程：

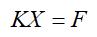
将之转化为实数系统：

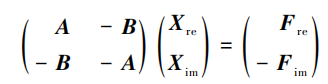
其中：

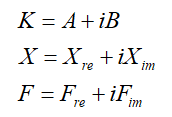
接下来，构造预条件矩阵M，将原始矩阵的实部虚部相加，此时的M矩阵既包含了原始方程的所有信息：

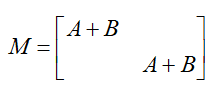
有了预条件矩阵，进一步需要求解关于Mz=v的内部方程，从M矩阵的构造可见，有两部分组成，并且一致，因此无论是使用直接求解还是迭代求解，这部分的内存相比于原矩阵会减小了一半。

但是直接求解该矩阵依然会有很大内存，为了避免直接求解，就有了辅助空间预条件AMS(Auxiliary space Maxwell Solver),该方法根据maxwell方程的特征构造而成，原理复杂，感兴趣参考相关文献。

该方法实现比较复杂，辅助空间预条件的理解困难，一般使用HYPRE程序库提供的接口实现，但是即使提供了接口，难度依然很高。

本文从开源代码中把这部分提取出来，分析并简化接口，以方便后续工程中直接调用，降低该方法的使用门槛。

二、安装环境

建议在ubuntu下配置环境，基于petsc环境库直接安装所有依赖环境，一步到位。其它环境可能安装会因为本身版本等原因安装困难。

git clone -b release https://gitlab.com/petsc/petsc.git petsccd petsc# 1. 配置：下载并编译 MUMPS + HYPRE + SuperLU_DIST + 相关依赖./configure \  --COPTFLAGS="-O3" --CXXOPTFLAGS="-O3" --FOPTFLAGS="-O3" \  --with-debugging=0 \  --with-shared-libraries=1 \  --download-mpich=1 \  --download-mumps=1 \  --download-hypre=1 \  --download-superlu_dist=1 \  --download-metis=1 \  --download-parmetis=1 \  --download-scalapack=1 \  --download-cmake=1 \  --prefix=$HOME/petsc-install
# 2. 编译 & 安装make -j$(nproc) allmake install

三、数据接口数据

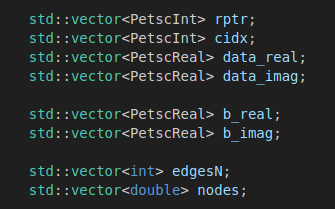
不考虑AMS的内部实现过程，单从所需要的数据考虑，对于一阶矢量有限元而言，共计需要五个数据：

标准的CSR格式的行个数、列索引、非零原始实部虚部、右端项实部虚部；网格信息：棱边到节点的映射关系、节点的坐标信息。

FGMRES-AMS整个代码流程：

1.初始化petsc与配置ams选项信息；2.填入接口数据；3.创建pestc线性系统，分配内存；4.将数据填入pestc 专用矩阵中；5.创建预处理器，包括ams的G矩阵；6.求解线性方程组;7.输出结果;8.释放空间，结束;

整个流程中，只需要把2步骤填写好即可求解，其他部分均封装好不用过多处理。

四、测试案例

输入一个matlab中已有的三维矢量有限元求解电场的稀疏矩阵。使用FGMRES-AMS求解，测试结果是否与matlab 直接求解结果一致。

测试信息，矩阵维度是3124个未知数：

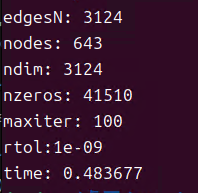
测试结果，25次迭代完成。

求解结果与matlab结果一致。下面展示下不同情况下的计算效率：

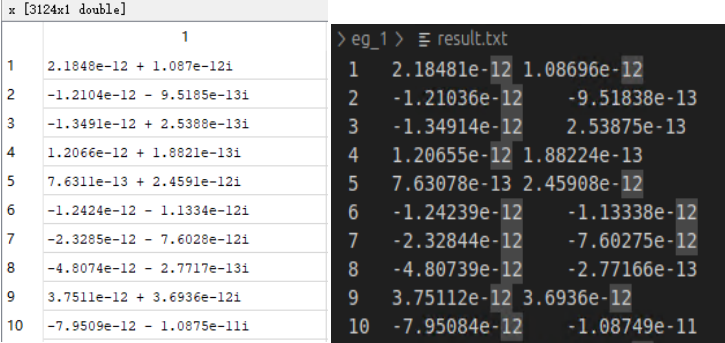
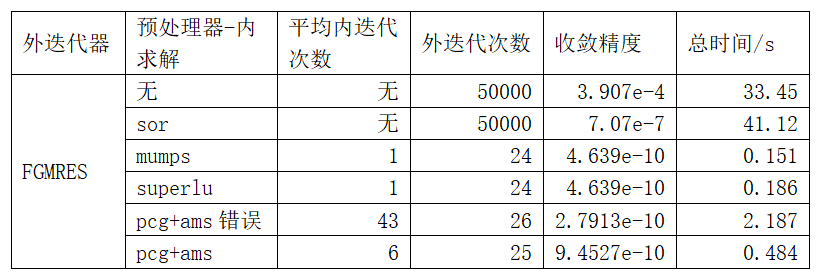
对比结果，仅使用外循环FGMRES，不使用预处理器完全无法收敛，使用传统的sor简单处理收敛精度也只能达到1e-7次方量级，但是依然无法完全收敛，并且迭代次数已经达到5万次，收敛的时间也在半分钟左右。对于这个自由度在3000左右的矩阵速度是非常慢的。

而使用了M预处理矩阵，无论预处理矩阵怎么求解，均可以收敛到1e-10次方量级，并且计算效率远高于不使用预处理矩阵。即使AMS的组装错误，其求解的时间也远低于无预处理的情况。

对于使用mumps、superlu、PCG+AMS对预处理矩阵求解,效果非常好，基本上在一秒以内完成计算。本例子中预处理直接求解的效率高于AMS是由于案例规模确实太小，如果矩阵规模更大，AMS的优势会慢慢体现。

总体上可以得出结果，本次的FGMRES+AMS的求解流程是正确的，基本上外循环在25次左右就完全收敛。

总结

1.本文意在让复杂的FGMRES+AMS简单化，易于后期使用；

2.值得注意的是，该求解器依赖于剖分网格，因此对于高阶有限元而言，处理情况更加复杂，开源软件MFEM中似乎已经集成了高阶情况下FGMRES+AMS求解器。

参考文献：

1.《基于自适应矢量有限元法的三维大地电磁正反演研究》

2.《面向实际地质情况的可控源电磁各向异性三维大规模并行正反演》

来源：实践有限元

有限元区域分解：Schwarz迭代法-二维泊松方程

简述对于区域分解技术有很多实现方法，在上篇文章中介绍的方式有限元区域分解技术入门级实现-泊松方程是通过对耦合边界强加连续性边界条件的方式实现区域之间的耦合。本文中提及区域分解方法是更为常见的Schwarz迭代方法，它是通过交替求解子区域问题并更新边界信息实现全局求解。下面主要介绍Schwarz的关键点。1.边值问题求解最简单的二维泊松方程：右端项为：解析解：泊松方程对应的有限元弱形式：采用三角形网格剖分，将整个研究域剖分为具有重叠区域的两个区域，如下图：红色区域1和蓝色区域2在中间部分重叠。分别独立组装区域1，区域2的系数矩阵和右端项，此时流程与传统有限元组装一模一样。需要注意，加载边界条件的时候，使用实际的全局边界条件。具体有限元组装方式这里不再讨论，可参考：有限元文章集合-2024年2.Schwarz交替迭代交替迭代的原理：在区域1上求解：此时u2在区域1边界上的解作为已知信息，迭代得到新的u1；在区域2上求解：此时u1在区域2边界上的解作为已知信息，迭代得到新的u2;二者交替迭代，直到最终前一次解u1、u2和当前解u1、u2完全收敛为止。详细的公式推导，区域1上的求解公式：迭代中，已知u1,b的值，因此，上述式子进一步推导：子域中本质上是求解上述方程，右端项是随着迭代过程，不断的被区域2的解进行修正。区域2上求解过程与区域1完全一致：最终判断各自区域的解收敛条件，满足以下条件：3求解结果针对以下网格，重叠区域有4列网格。虽然网格棱边并不完全重合，但是节点有限元不关心棱边，仅关系节点，因此无影响。迭代结果：iter1:error=11.7089iter2:error=2.45967iter3:error=0.200195iter4:error=0.0162943iter5:error=0.00132622iter6:error=0.000107944iter7:error=8.78578e-06iter8:error=7.15092e-07iter9:error=5.82028e-08iter10:error=4.73724e-09结果显示：使用区域1（红色圆圈），区域2（红色三角形），全域有限元（蓝色加号）分别求解得到u然后和理论解析解对比，在x方向显示，如下：可以发现，红色和蓝色的误差分布基本上在一个量级，说明区域分解能和全域求解达到一个量级。此外细心还可以发现，红色圆圈和红色三角形在中间区域的各自边界上的解的误差是一致的，说明其本身的解也是一致的，这也是迭代的结果，前一次的区域2的解是作为第一类边界条件加入到区域1中的。下面测试不同重叠区域对收敛次数的影响：其对应的收敛到1e-8以下的迭代次数如下表格：可以发现，基本上符合原理，重叠越大，迭代次数越少，但是必须得有重合，否则耦合区域没有点可供更新。最后重叠形Schwarz迭代，其本质是通过重叠区域交换信息，重叠区域越大，收敛越快，但是对应的计算成长更高。迭代过程中可以发现，每次迭代过程均需要子域求解一次方程，但是K系数矩阵是没有变化的，因此只需要求解一次LU分解即可，后续更新回代不同的右端项即可。相比于上一篇文章提及的方法，本文方法或许效率还更高一些，因为上一篇文章提及的方法需要矩阵求逆，并且子域求解完，组装的所有边界相关的矩阵也需要解方程。来源：实践有限元