涡轮丨703所:某船用燃气轮机涡轮盘疲劳裂纹扩展寿命预测研究
为提高船用燃气轮机涡轮盘的寿命设计水平,基于数值仿真方法对涡轮盘开展典型循环载荷作用下应力应变状态分析,并通过Morrow平均应力修正模型和SWT参数模型对涡轮盘裂纹萌生位置及寿命进行预测。在此基础上,进一步对涡轮盘高温合金材料开展不同温度下疲劳裂纹扩展试验,建立涡轮盘裂纹扩展速率模型,通过ANSYS软件和裂纹扩展程序仿真研究裂纹扩展寿命。结果表明:涡轮盘通气孔位置为裂纹萌生的危险位置,涡轮盘材料裂纹扩展速率随温度升高而明显增加,涡轮盘通气孔疲劳裂纹扩展寿命为18525次循环,研究结果可为燃气轮机涡轮盘损伤容限设计提供参考。
关键词:燃气轮机;仿真分析;低周疲劳;裂纹扩展;疲劳寿命
引言
引言
涡轮盘作为船用燃气轮机的关键热端部件,在高温、高转速等恶劣环境下工作,承受着转子质量带来的离心力和温度梯度产生的热应力等典型载荷。在非对称循环载荷持续作用下,轮盘的中心孔、通气孔及螺栓连接孔等几何不连续位置容易萌生低周疲劳裂纹并持续扩展,进而造成涡轮盘破裂失效。燃气轮机涡轮盘破裂会造成非包容性破坏等后果,因此准确地预测轮盘的低周疲劳寿命十分关键,对结构损伤容限设计、保证轮盘结构完整性具有重要意义。
国内外学者针对不同旋转机械结构的裂纹扩展问题开展了大量的研究。Claudio等人针对裂纹尖端网格划分难题,提出了一套针对单元类型选取以及网格生成方法等问题的解决方案,经真实燃气轮机涡轮盘试验数据验证,证明了有限元方法在估算燃气涡轮盘寿命方面具备巨大潜力。Beres等人在Nene-X发动机涡轮盘应力分析的基础上,通过概率断裂力学方法对断裂关键位置进行了预测,确定了安全检查间隔。文献在国际合作项目支持下对涡轮转子部件进行裂纹扩展仿真及试验验证,通过对比4款裂纹扩展软件的预测结果,针对复杂零件的几何形状、有明显载荷再分布的零件或线弹性假设不成立的情况,推荐使用ZENCRACK和FRANC3D计算软件,并通过试验验证重新确定燃气涡轮发动机转子关键件低周疲劳寿命。Farukh等人建立了粘塑性本构模型,预测镍基高温合金在保载-疲劳作用下的裂纹扩展行为,通过扩展有限元方法预测裂纹,扩展结果与试验数据高度一致。聂景旭针对某发动机涡轮盘槽底裂纹,提出一种先按照线弹性计算复杂载荷作用下的J积分,再进行塑性修正的“二次计算法”,并得出确定涡轮盘临界裂纹长度的准则和方法。王革等人[9]针对服役后的涡轮盘出现槽底裂纹的问题,分析了J积分随裂纹长度和转速变化的规律,研究确定涡轮盘临界裂纹长度和扩展寿命。刘绍伦等人对钛合金材料和燕尾槽子构件开展疲劳试验研究,并采用塑性诱导的Newman裂纹闭合模型,建立了萌生裂纹的燕尾槽槽底疲劳全寿命预测模型。陆山等人采用双重边界元法计算涡轮盘三维裂纹强度因子,结合Paris公式及Euler法获得涡轮盘销钉孔边裂纹扩展形状及裂纹扩展寿命。魏大盛等人通过J积分方法对粉末冶金拉伸试样和涡轮盘开展裂纹扩展寿命评估,并根据粉末盘缺陷分布概率建立了失效模式的可靠度计算模型。张智轩等人采用FRANC3D分析了压气机轮盘销钉孔多种裂纹形式对轮盘寿命的影响。邹昱申等人针对某GH4169动力涡轮盘开展三维角裂纹扩展过程的仿真分析及试验研究,结果表明,裂纹前沿扩展形状及扩展速率与试验结果较一致。吴英龙等人通过对涡轮盘裂纹扩展仿真及低周疲劳试验断口的分析,获得了高温合金多源疲劳裂纹扩展特征。
目前,国内关于旋转机械部件裂纹扩展的研究多针对航空发动机轮盘,对船用燃气轮机轮盘损伤容限的研究较少。本文采用Morrow平均应力修正模型和SWT参数模型对燃气轮机涡轮盘裂纹萌生的危险位置及寿命进行预测。通过开展涡轮盘材料高温疲劳裂纹扩展试验,建立了涡轮盘裂纹扩展速率模型,并根据涡轮盘通气孔和中心孔开展疲劳裂纹扩展分析,确定出现可检裂纹后的涡轮盘的剩余寿命。
计算方法
计算方法
1.1 裂纹萌生寿命计算方法
Coffin-Manson应变寿命模型具有物理含义明确、疲劳参数获取简单等特点,是工程中最常用的低周疲劳寿命预测模型,Coffin-Manson公式如下:

大量研究表明,平均应力小于零时,疲劳寿命增加;平均应力大于零时,疲劳寿命降低。由于CoffinManson公式是基于对称循环载荷条件获得的,无法考虑平均应力对疲劳寿命的影响,因此众多学者提出许多平均应力修正模型,经典的修正模型有Morrow平均应力修正模型及SWT参数模型,本文通过这两种平均应力修正模型开展裂纹萌生寿命评估。
Morrow平均应力修正模型是在工程中最常用的Coffin-Manson应变寿命分析模型的基础上,考虑平均应力的影响,对弹性应变部分进行修正,修正后的应变寿命方程如下:
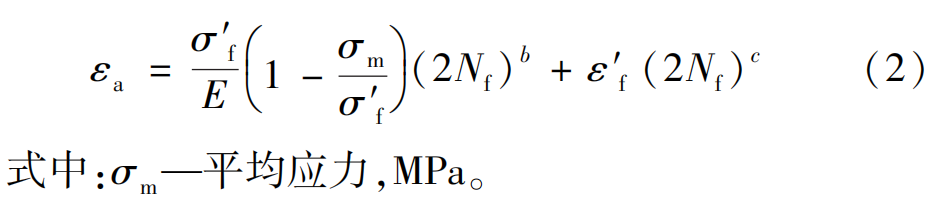
SWT参数模型是Smith、Watson和Topper等人提出的一种假设任意平均应力下的寿命取决于最大应力与应变幅值乘积的模型,与大量的试验结果对比发现,该模型对很多材料的寿命预测有较好的精度,其表达式如下:
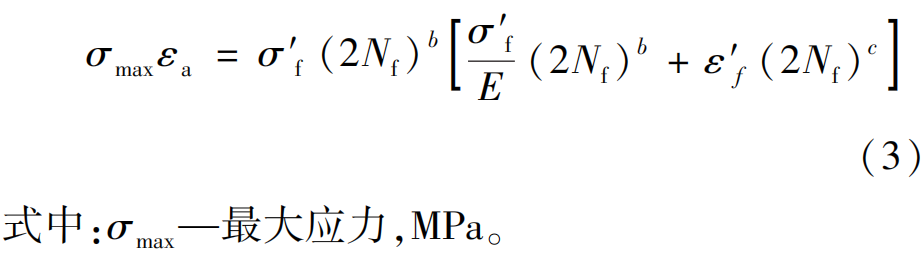
1.2 裂纹扩展计算模型
Paris和Erdogan在试验的基础上提出了Paris公式,此公式描述了裂纹扩展速率与应力强度因子范围之间的关系,其表达式如下:

式中:da/dN—疲劳裂纹扩展速率,mm/循环;△K−应力强度因子范围,MPa⋅m1/2;C—疲劳裂纹扩展系数;m—疲劳裂纹扩展指数,通过试验数据拟合获得。
此后大量学者的相关研究也表明裂纹扩展速率da/dN与ΔK的呈高度正相关,说明ΔK作为裂纹扩展驱动因素可以较好地描述裂纹扩展速率,目前在工程中Paris公式仍然是应用最广泛的预测模型。
涡轮盘危险位置疲劳裂纹萌生寿命预测
涡轮盘危险位置疲劳裂纹萌生寿命预测
2.1 涡轮盘强度分析有限元模型
本文研究的涡轮盘材料为某镍基高温合金,为评估涡轮盘关键位置疲劳寿命,采用ANSYS有限元软件对某燃气轮机涡轮盘的应力及应变状态进行分析,图1为涡轮盘几何模型及有限元模型。
涡轮盘含有10个通气孔,为提高计算效率,选取1/10循环对称模型进行计算分析,单元类型为Solid187,施加温度载荷及离心力载荷,约束连接端面的轴向及周向位移为零。
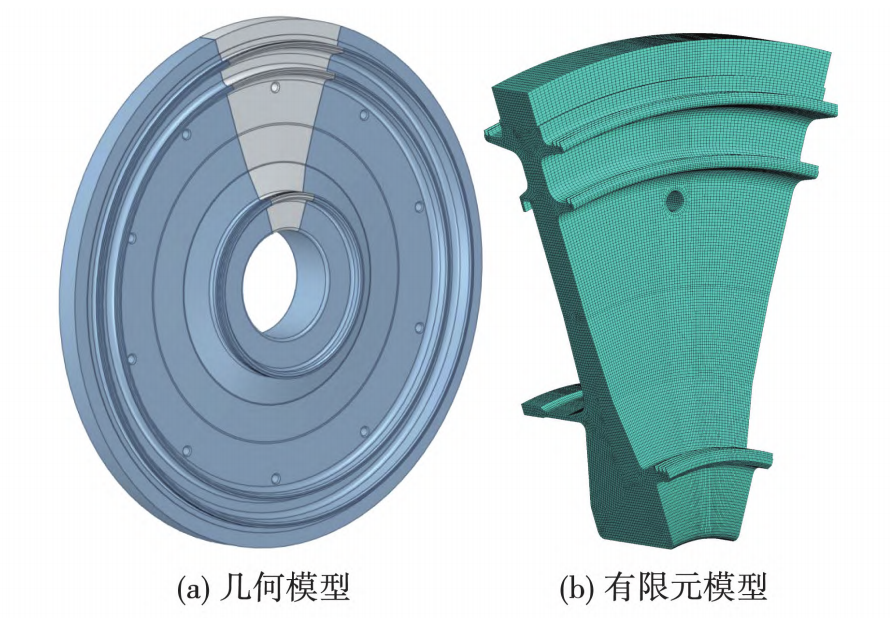
图1 涡轮盘几何模型及有限元模型
2.2 涡轮盘强度分析结果
针对涡轮盘额定转速工况及卸载受力状态进行弹塑性计算分析,涡轮盘材料的力学性能如表1所示。
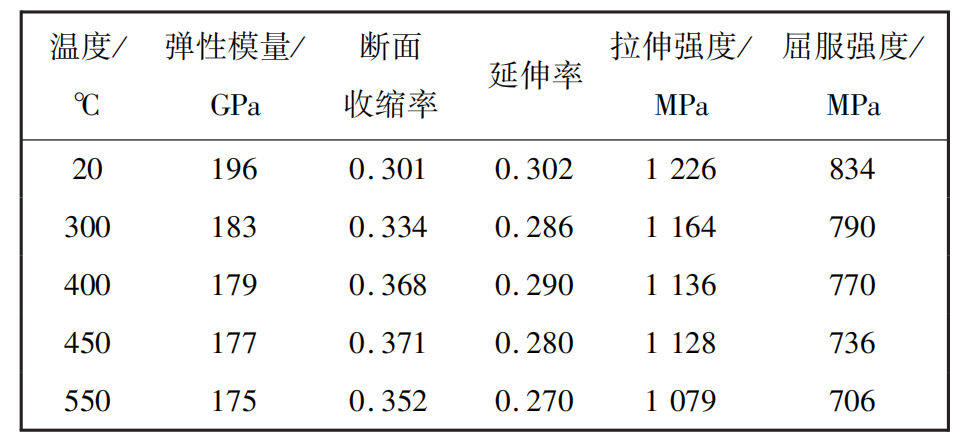
表1 涡轮盘材料的力学性能
通过仿真计算得到涡轮盘通气孔温度为450℃,最大等效应力为738MPa;中心孔温度为300℃,最大等效应力为745MPa。确定涡轮盘通气孔和中心孔为重点考察位置,等效应力分布情况如图2和图3所示,其受力状态为拉应力主导。
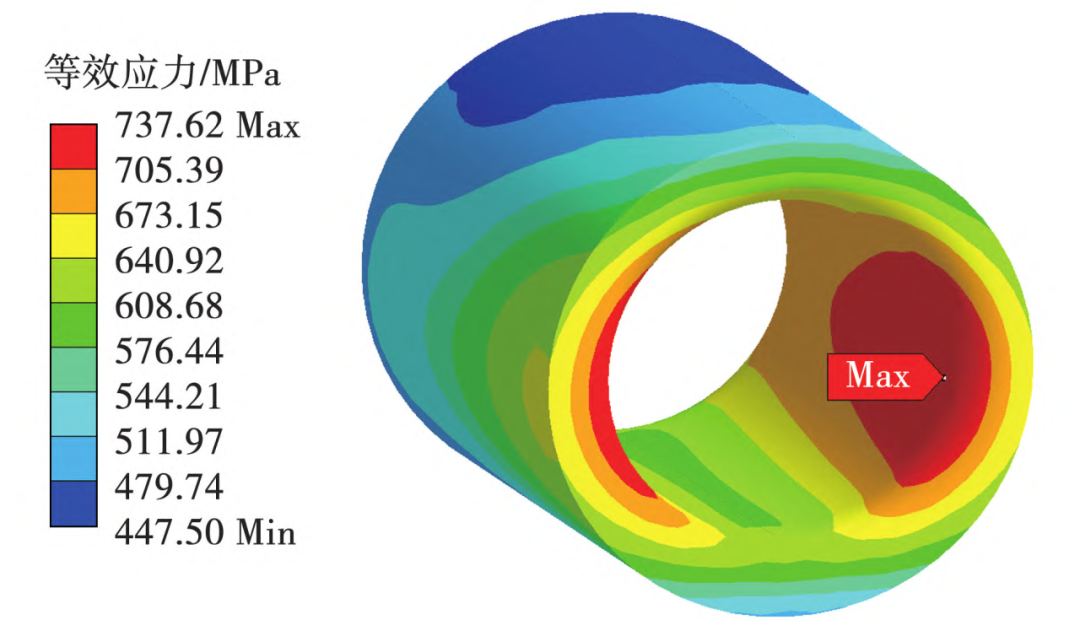
图2 涡轮盘通气孔等效应力分布
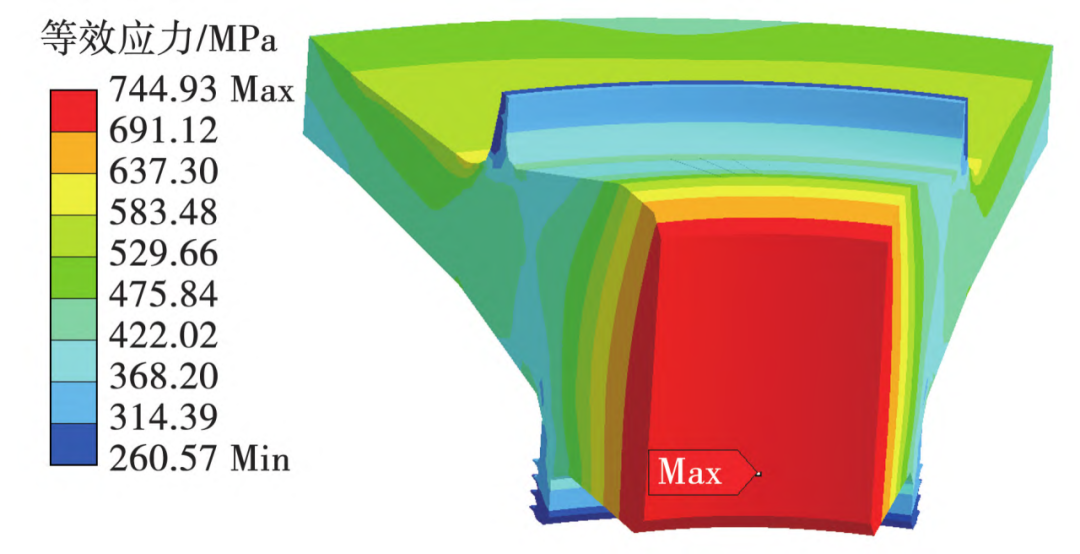
图3 涡轮盘中心孔等效应力分布
2.3 涡轮盘危险位置疲劳裂纹萌生寿命预测结果
根据王延荣等人发展的方法,利用表1中的数据对应变寿命方程中的疲劳参数进行估算,得到涡轮盘材料疲劳参数如表2所示。
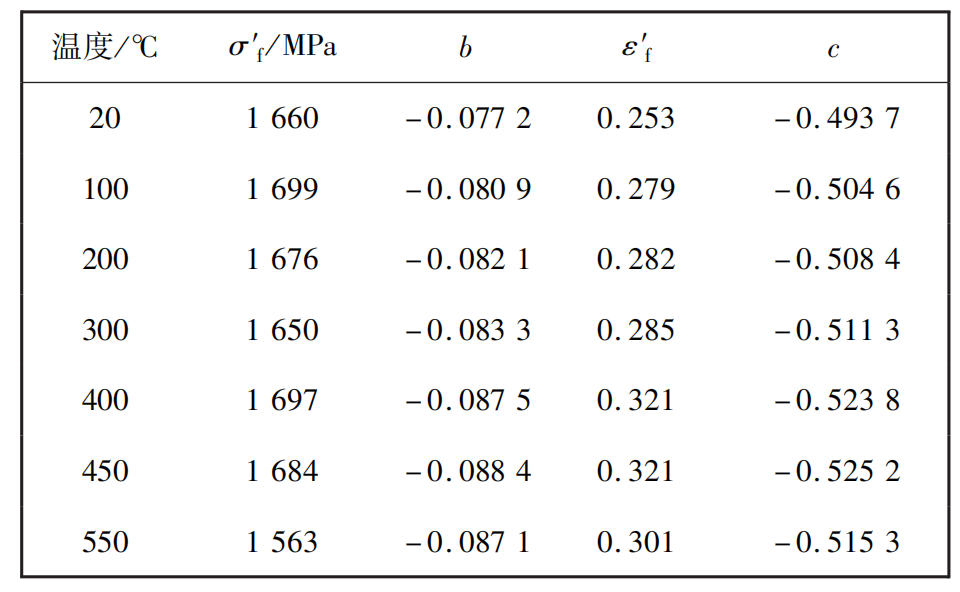
表2 涡轮盘材料疲劳参数
根据强度分析结果,确定通气孔和中心孔为低周疲劳寿命预测关键位置。采用Manson-McKnight修正法将多轴应力应变分别等效为单轴应力应变,通过Morrow平均应力修正模型及SWT参数模型对涡轮盘疲劳寿命进行预测,结果如表3所示。
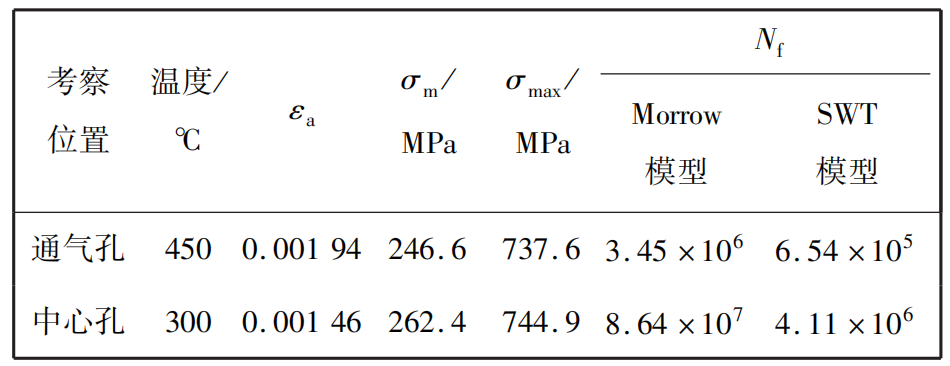
表3 轮盘危险位置寿命预测结果
由表3可知,两种模型预测结果均表明涡轮盘最低疲劳寿命位于通气孔处,其中,Morrow平均应力修正模型预测寿命为3.45×106,SWT参数模型预测寿命为6.54×105,根据上述计算结果可以判定通气孔为裂纹萌生的主要考核位置,中心孔为裂纹萌生的次要考核位置。
涡轮盘裂纹扩展寿命预测
涡轮盘裂纹扩展寿命预测
根据2.2节和2.3节分析结果可知,涡轮盘疲劳裂纹可能出现于涡轮盘通气孔和中心孔位置,为进一步分析轮盘损伤容限,开展涡轮盘材料疲劳裂纹扩展速率试验和涡轮盘裂纹扩展寿命预测。
3.1 涡轮盘材料疲劳裂纹扩展速率试验
按照标准GB/T 6398-2017,开展涡轮盘材料裂纹扩展速率试验,试验件为标准紧凑拉伸试样(CT试样),试样厚度B为10mm,标称宽度W为50mm,缺口长度an为7.5mm,试样尺寸如图4所示。利用PLG-100疲劳试验机对预制3mm初始裂纹的CT试样进行拉-拉疲劳试验,加载频率为10Hz,波形为正弦波,采用柔度法测量裂纹扩展中的裂纹长度,得出试验所测裂纹扩展速率曲线。
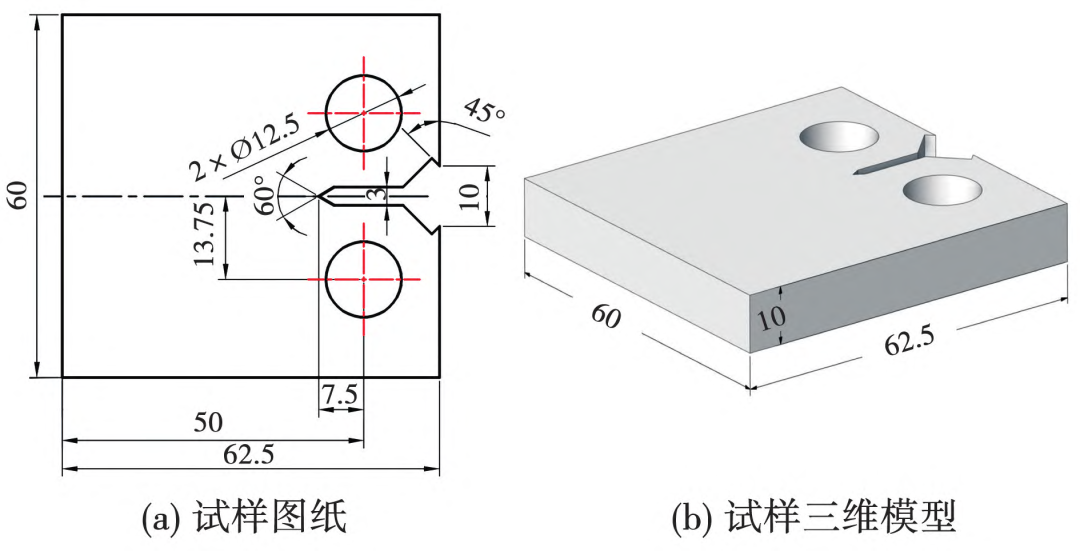
图4 紧凑拉伸试样(CT试样)尺寸示意图
在试验过程中,保载载荷Fmax为9.5kN,应力比R为0.1,考虑涡轮盘工作温度范围,分别在300和600℃条件下开展裂纹扩展速率试验,得到的裂纹扩展速率与应力强度因子范围曲线如图5所示。
由图5可知,试验测得数据集中于稳态裂纹扩展区,选择Paris公式作为裂纹扩展速率表达式,经线性拟合获得不同温度下裂纹扩展系数C和指数m如表1所示。
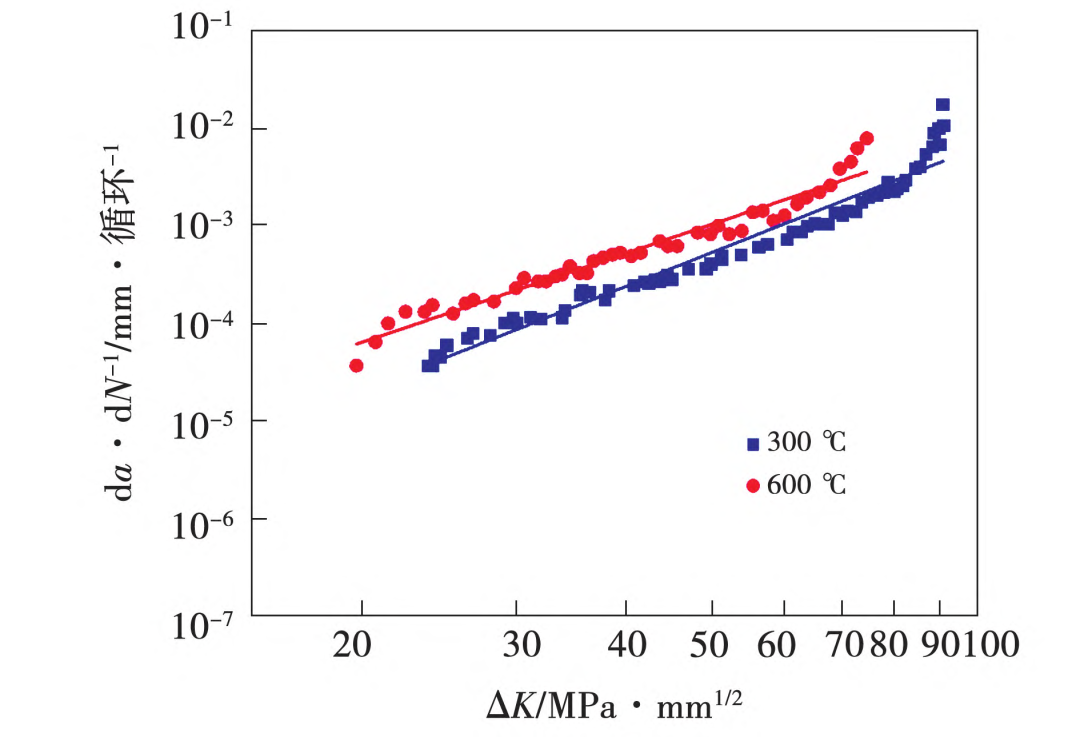
图5 裂纹扩展速率与应力强度因子范围曲线

表4 不同温度下Paris公式中参数C和m
3.2 裂纹扩展分析模型
本文使用ANSYS软件及裂纹扩展计算程序对涡轮盘进行裂纹扩展仿真研究,仿真分析流程如图6所示。
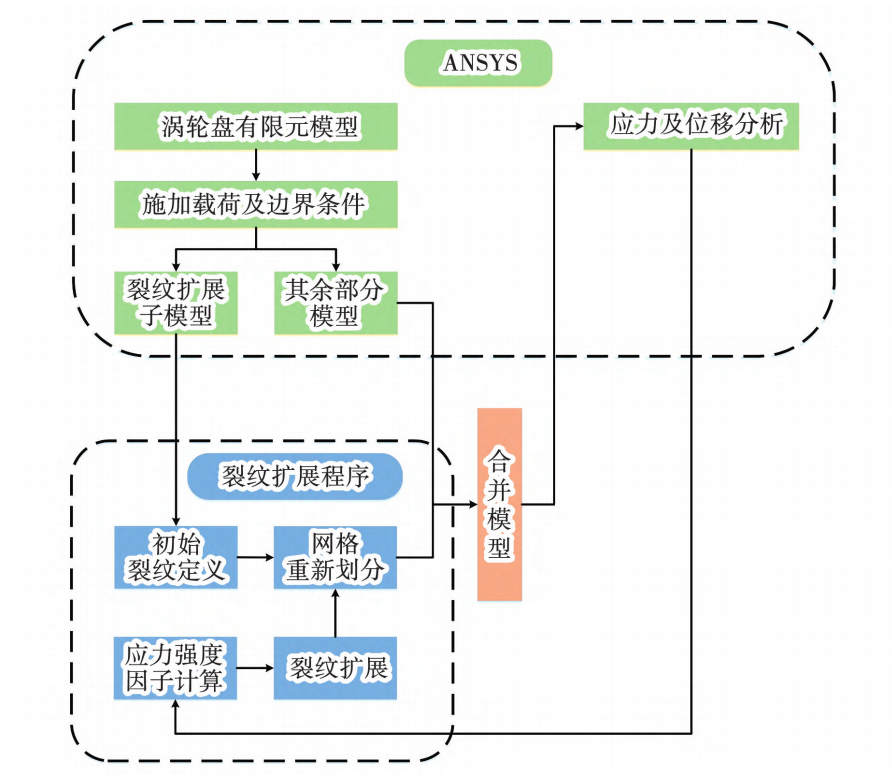
图6 裂纹扩展仿真分析流程
根据涡轮盘有限元及裂纹萌生寿命预测结果可知,裂纹萌生于通气孔和中心孔的可能性最大。为提高计算效率,将有限元模型划分为裂纹扩展区域(子模型)和非裂纹扩展区域(全局模型),裂纹扩展在子模型上进行,全局模型及子模型剖分边界面上的网格在迭代分析中保持不变,子模型与全局模型通过绑定剖分边界节点整合为完整的计算模型。首先对通气孔和中心孔位置进行局部剖分,分别建立子模型进行裂纹扩展分析。其中,涡轮盘全局模型、通气孔子模型和中心孔子模型网格划分如图7所示。
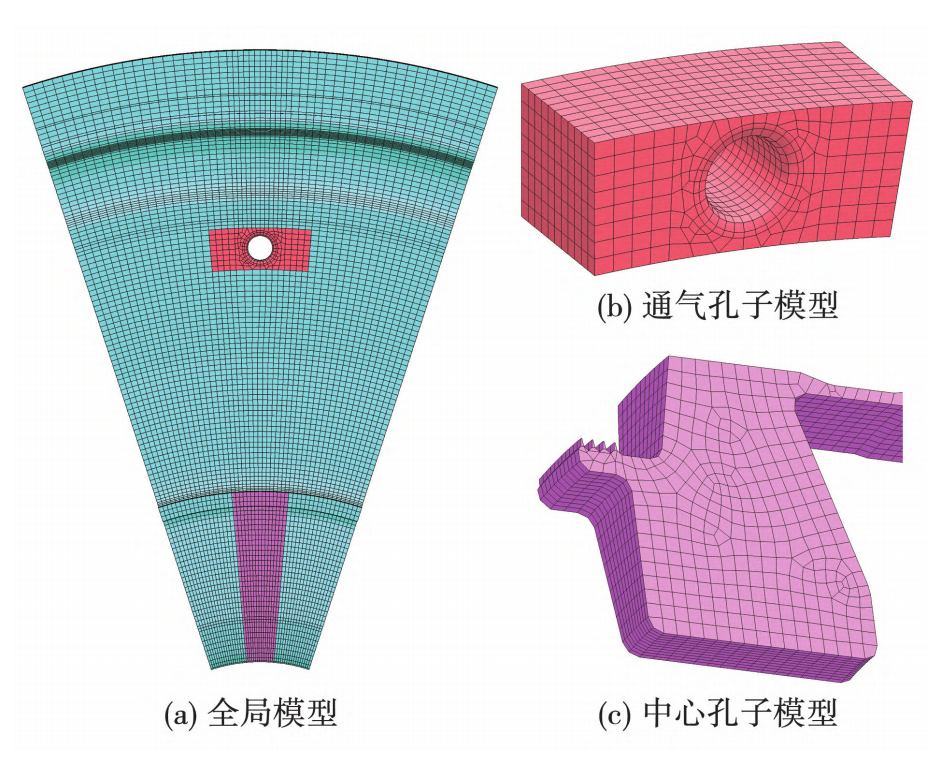
图7 考核位置模型网格划分
3.3 涡轮盘危险位置疲劳裂纹扩展寿命预测结果
将前文用于强度计算的有限元模型的.cdb文件导入裂纹扩展计算程序中,沿轴线方向在通气孔和中心孔等效应力最大的位置分别插入裂纹长度为0.76mm的圆形表面裂纹,根据插入的裂纹对子模型网格进行重新划分,网格划分情况如图8和图9所示。
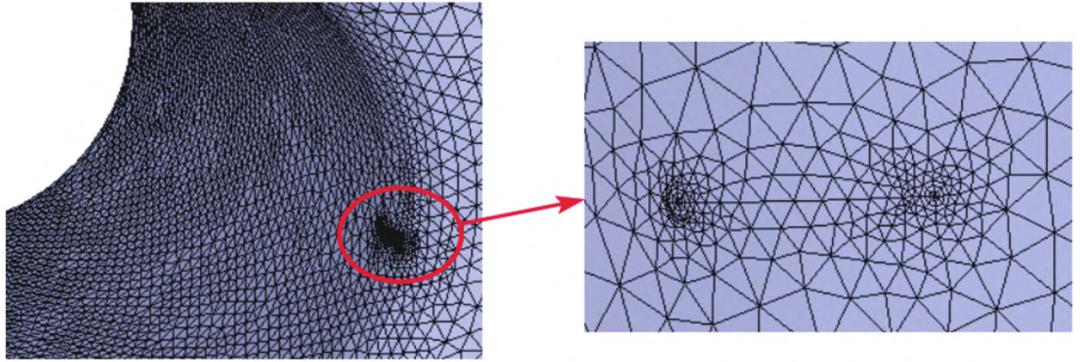
图8 通气孔初始裂纹位置及网格重新划分
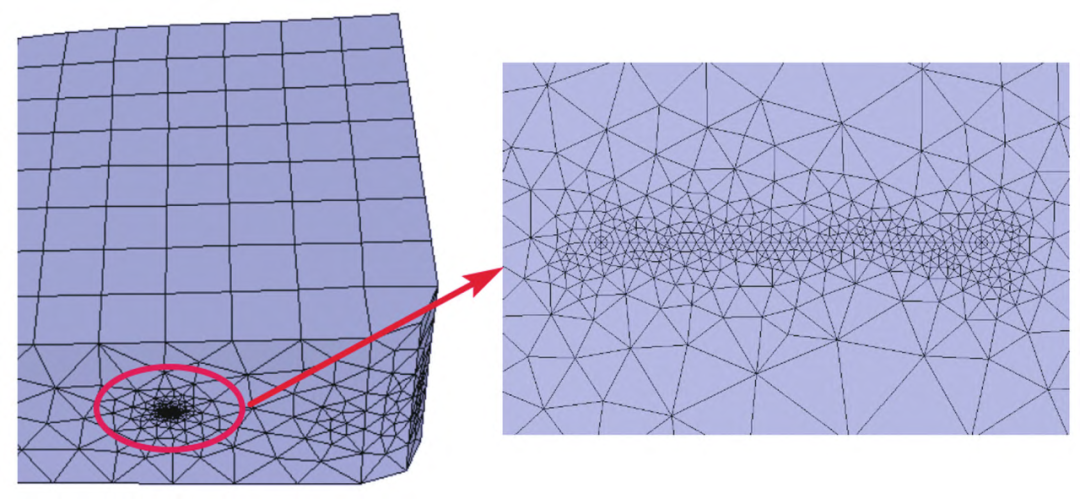
图9 中心孔子模型有限元网格重新划分
计算预置裂纹尖端所有节点的应力强度因子,得到的应力强度因子反映出裂纹尖端弹性应力场的强弱,通气孔和中心孔裂纹尖端对应的不同开裂方式的3类应力强度因子值如图10和图11所示,从图中可以看出,应力强度因子KⅠ大于KII和KⅢ,因此可以认为涡轮盘这两个位置裂纹均为张开型裂纹,这与强度计算分析结论一致。
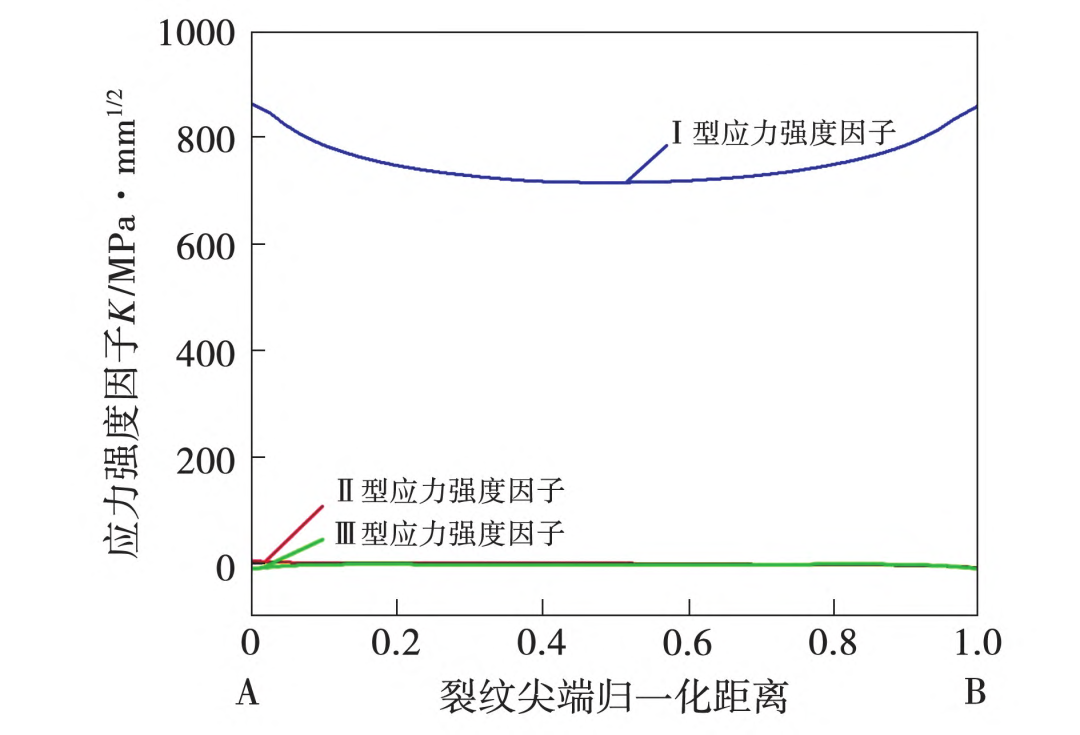
图10 通气孔裂纹尖端应力强度因子
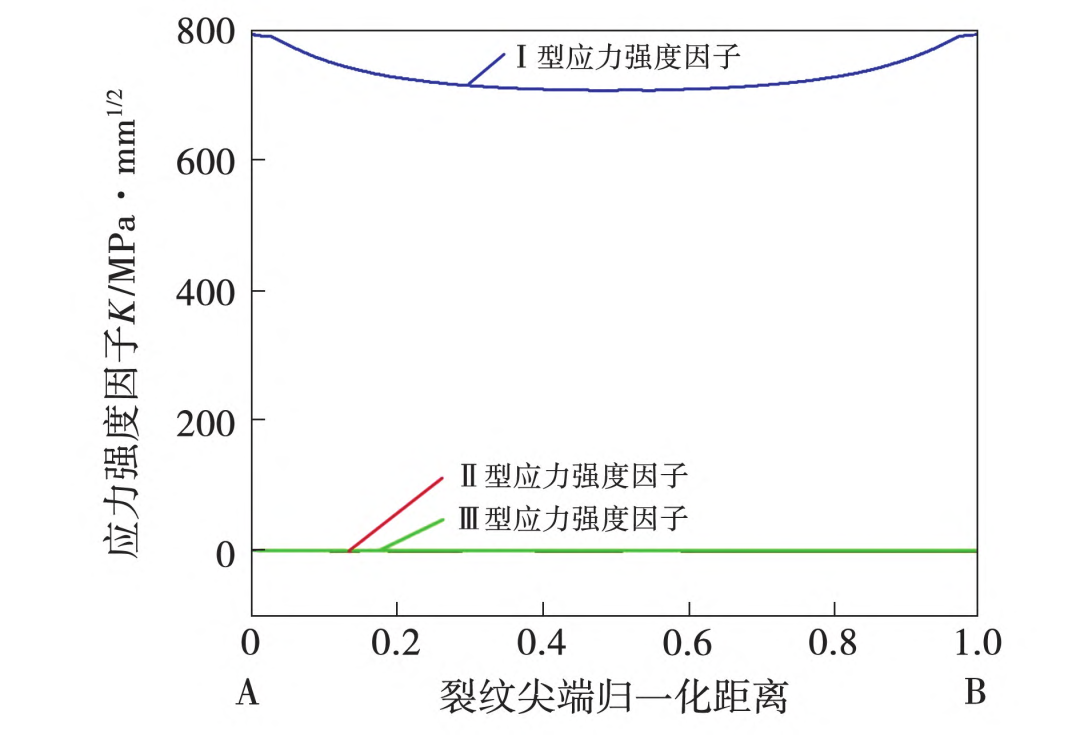
图11 中心孔裂纹尖端应力强度因子
本文关注的涡轮盘扩展寿命主要发生在裂纹稳态扩展阶段,在裂纹扩展计算程序中选择经典的Paris公式作为裂纹扩展速率模型,选用最大张应力准则作为裂纹扩展扭转角度计算准则,取应力比R=0.1。通气孔计算参数由300和600℃的参数插值获得,即C=1.58×10−9,m=3.34;中心孔计算所用参数C=4.24×10−10,m=3.59。基于ANSYS软件和裂纹扩展计算程序,采用M积分进行裂纹扩展分析,通气孔和中心孔裂纹扩展历程及裂纹形貌如图12和图13所示。计算中每个分析步对应的裂纹前缘如图中的弧线所示,通气孔裂纹沿轮盘轴向和周向扩展,中心孔裂纹沿轮盘轴向和径向扩展。
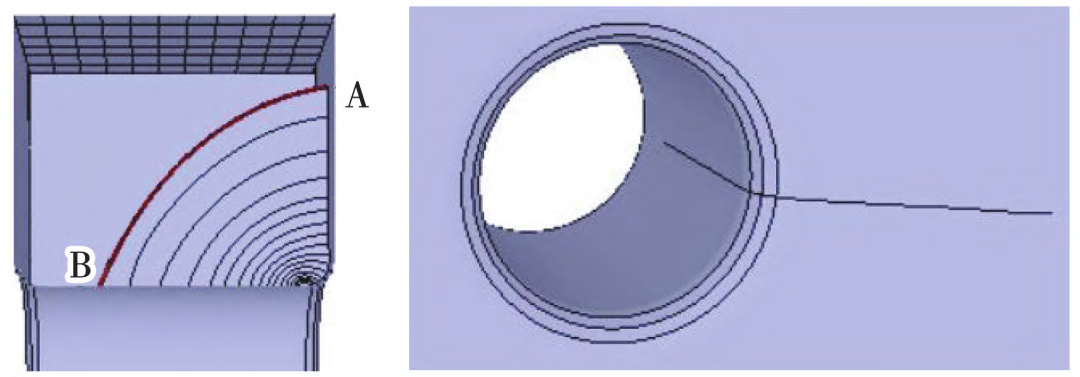
图12 通气孔裂纹扩展历程及裂纹形貌
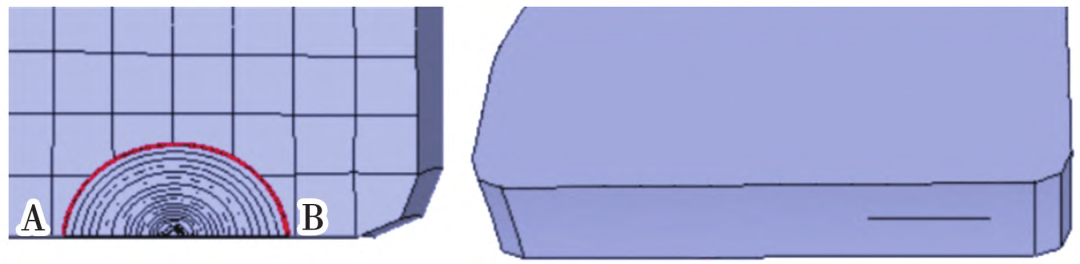
图13 中心孔裂纹扩展历程及裂纹形貌
图14和图15为通气孔和中心孔裂纹扩展过程中应力强度因子K₁随裂纹扩展历程变化情况。通气孔裂纹经过18个分析步(step)扩展,裂纹尖端应力强度因子达到断裂韧度2846MPa⋅mm1/2时,计算终止;中心孔裂纹经过21个分析步扩展,裂纹尖端应力强度因子达到断裂韧度3131MPa·mm¹/²时,计算终止。
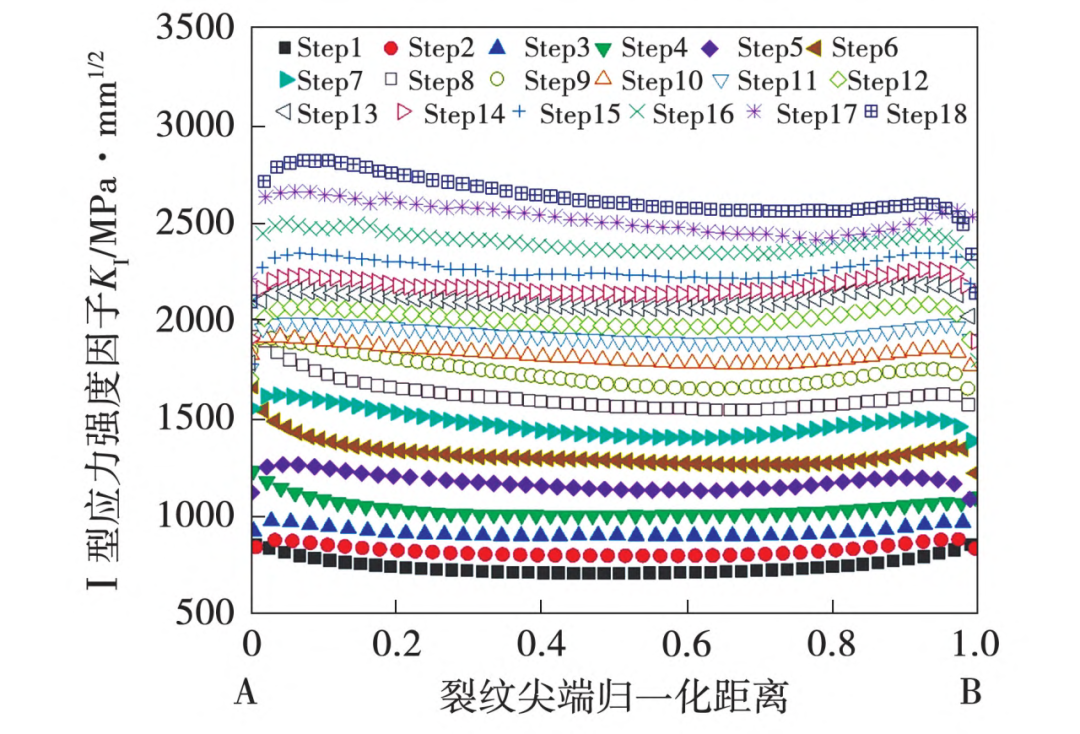
图14 通气孔应力强度因子K₁随裂纹扩展历程变化
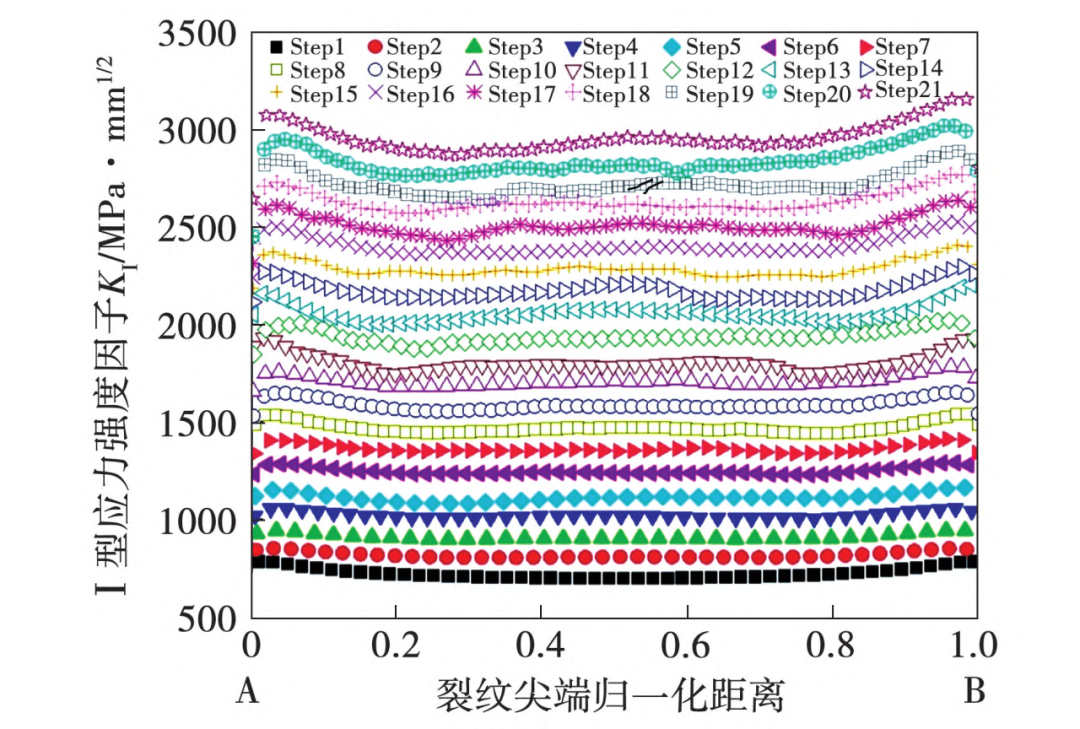
图15中心孔应力强度因子K1随裂纹扩展历程
通气孔和中心孔裂纹长度随循环次数的变化如图16所示。由图16可知,当通气孔经过18525次循环后,裂纹扩展至14.2mm;当中心孔经过20492次循环后,裂纹扩展至6.3mm。
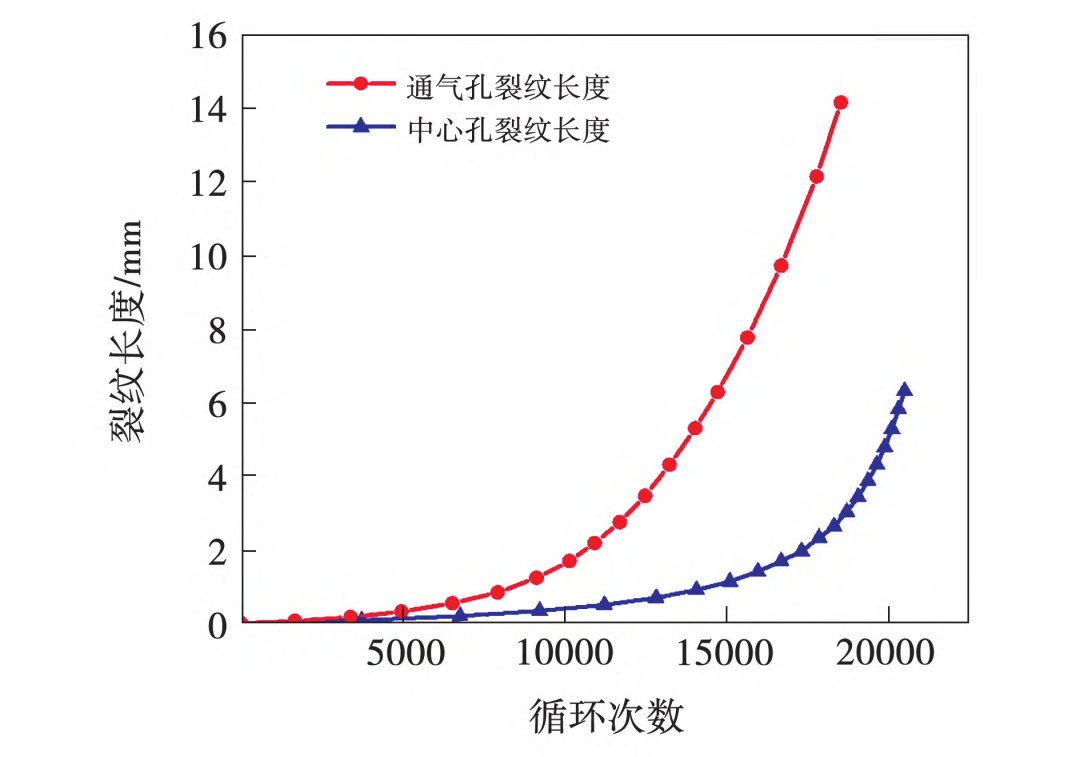
图16 裂纹长度随循环次数的变化
由于通气孔和中心孔裂纹强度因子已接近相应温度下材料的断裂韧度,可以判定通气孔为断裂失效的主要考核位置,中心孔为断裂失效的次要考核位置。在船用燃气轮机损伤容限设计及运维检修中需要重点关注通气孔和中心孔。
3.4 含初始损伤涡轮盘通气孔剩余寿命分析实例
所研究轮盘在加工制造过程中产生多条初始裂纹,裂纹情况如图17所示。为确定存在初始裂纹缺陷的轮盘能否继续开展燃气轮机图谱考核试验,需要对此裂纹扩展寿命开展计算评估。经无损检测结果确定最深的裂纹位于“3点钟”位置,裂纹深度约0.3mm,裂纹长度约12.5mm,同时此位置也是通气孔大应力区域,因此重点考察此位置的裂纹,在裂纹扩展软件中插入相应尺寸的长浅表面裂纹。
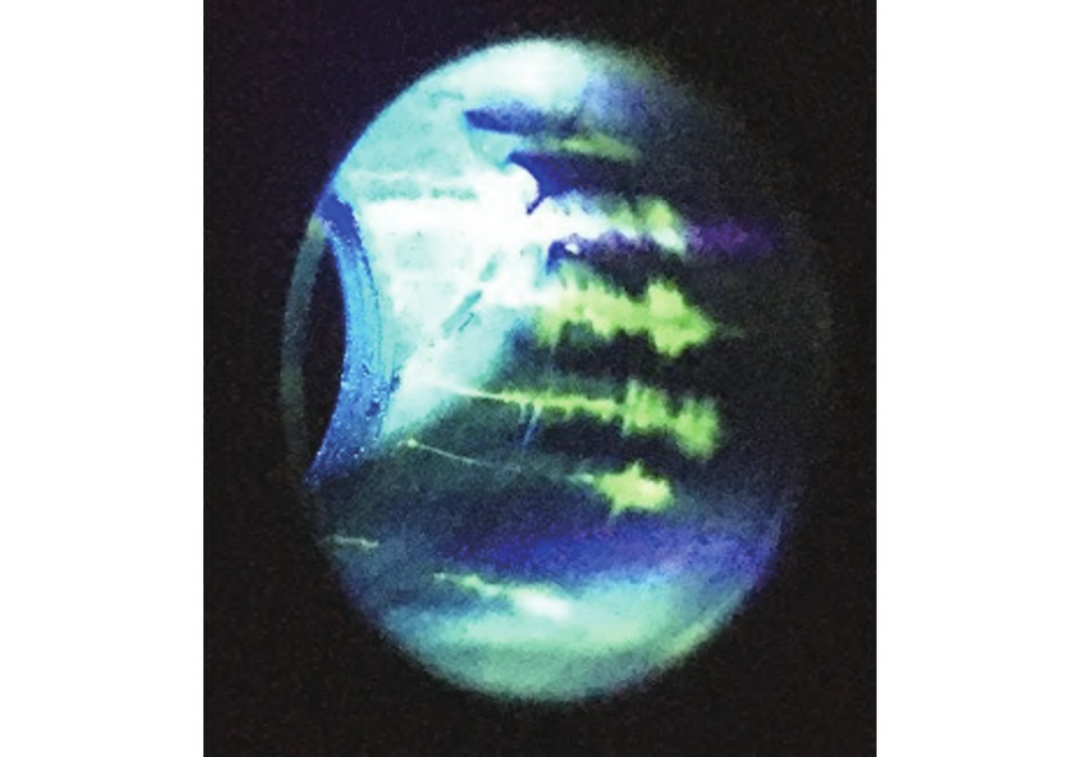
图17 加工造成的通气孔长浅裂纹
计算长浅裂纹尖端节点相应的应力强度因子,结果如图18所示,可以看出此裂纹同样可以认为是张开型裂纹。
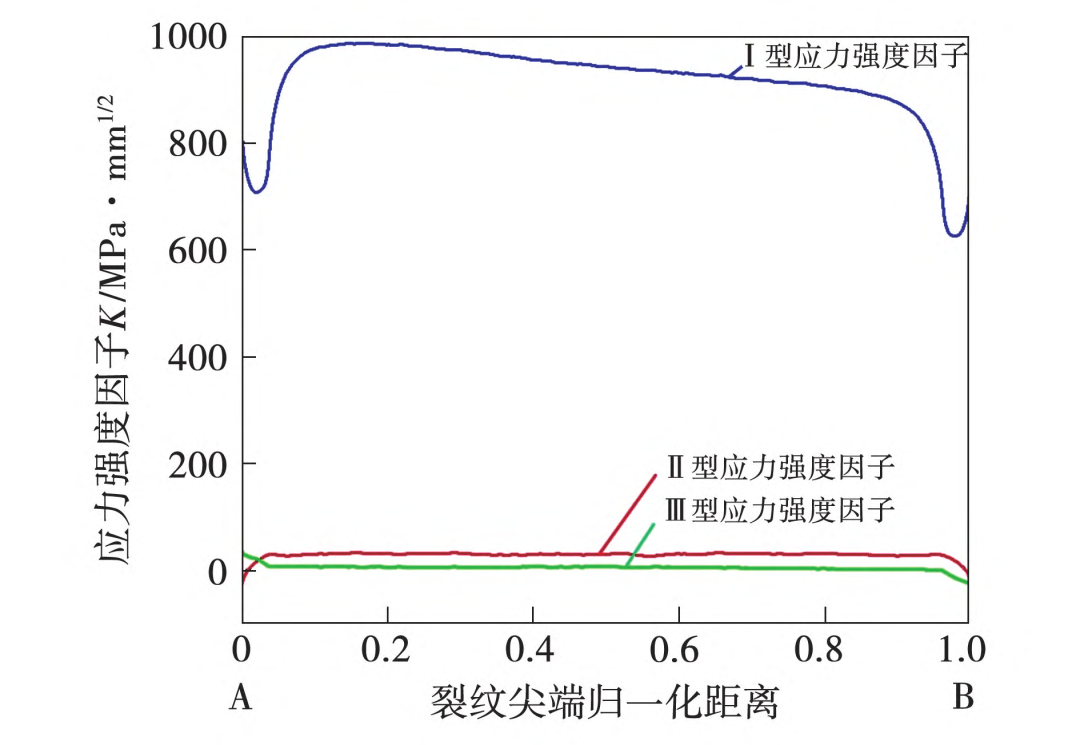
图18 长浅裂纹尖端应力强度因子
在裂纹扩展计算程序中进行通气孔长浅裂纹扩展分析时,计算设置与3.3节一致,计算得到的通气孔长浅裂纹扩展历程及形貌如图19所示。通气孔裂纹沿轮盘轴向和周向扩展,裂纹前缘由最初的通气孔内位置,最终扩展至轮盘辐板表面。
图20为通气孔长浅裂纹扩展过程中应力强度因子K₁随裂纹扩展历程变化情况。通气孔长浅裂纹经过17个分析步扩展,裂纹尖端应力强度因子达到断裂韧度2846MPa⋅mm1/2时,计算终止。
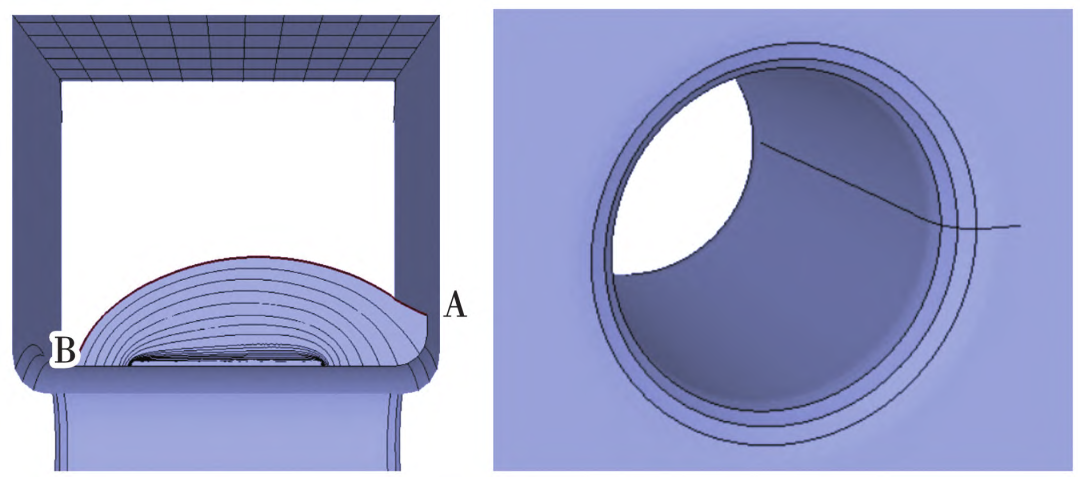
图19 通气孔长浅裂纹扩展历程及裂纹形貌
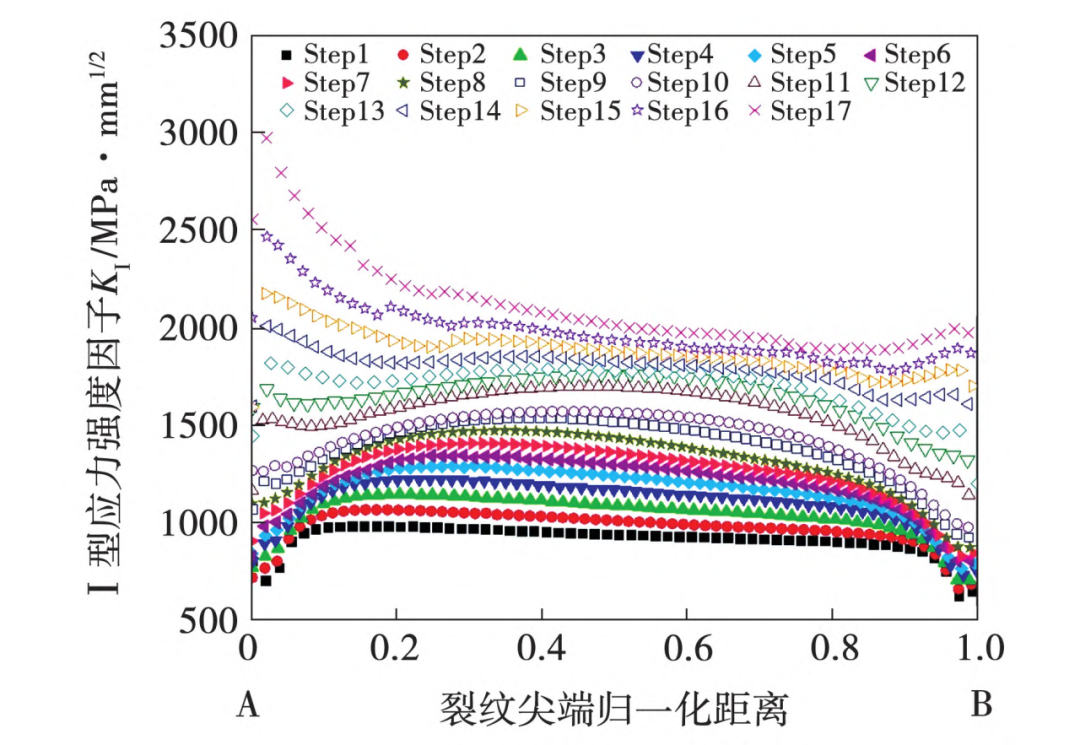
图20 通气孔长浅裂纹K₁随裂纹扩展历程变化
通气孔长浅裂纹长度随循环次数的变化如图21所示。由图21可知,当通气孔经过10181次循环后,裂纹扩展至8.2mm。
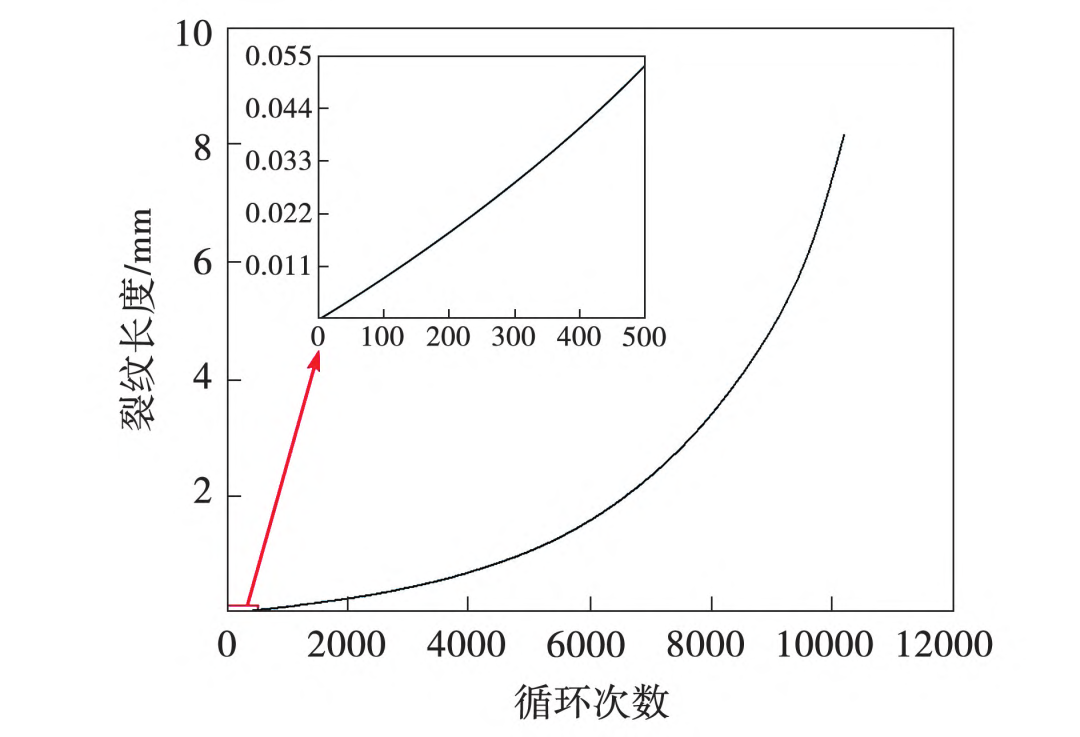
图21 通气孔长浅裂纹长度随循环次数的变化
轮盘考核试验循环数为200次,根据仿真结果可知,循环数达到200次时,裂纹扩展了约0.018mm,涡轮盘仍具有足够的剩余寿命,因此判断该轮盘可以继续用于试验考核。该轮盘顺利完成了燃气轮机图谱考核试验,初步验证了本文分析方法在船用燃气轮机领域的工程应用价值。
结论
结论
(1)对涡轮盘额定转速工况进行计算分析,确定涡轮盘通气孔最大等效应力为738MPa,中心孔最大等效应力为745MPa。
(2)采用Morrow平均应力修正模型和SWT参数模型对涡轮盘进行疲劳裂纹萌生寿命进行预测,结果表明SWT参数模型预测寿命偏为保守,但均表明涡轮盘最低疲劳寿命位于通气孔位置。
(3)通过标准紧凑拉伸试样开展涡轮盘材料裂纹扩展速率试验,获得300℃时疲劳裂纹扩展参数C=4.24×10−10,m=3.59;600℃时C=6.86×10−9,m=3.06 。
(4)通过ANSYS软件与裂纹扩展程序计算,确定通气孔经过18525次循环后,裂纹扩展至14.2mm,可以确定通气孔为断裂失效的主要考核位置。
(5)针对该涡轮盘在加工制造过程中产生的初始裂纹,开展了裂纹扩展寿命分析,并通过图谱考核试验验证了该分析方法在工程应用的重要价值。
声明: 本文来源于网络, 仅供交流分享, 若涉及版权等问题请留言, 我们会及时处理





