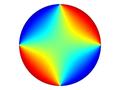
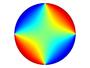
Comsol小技巧| 12-如何求解2阶微分方程?
Q
如何求解高于 2 阶的 PDE?比如求解 U(x,y)的方程 uxxxx + uxxyy+ uyyyy = f?
A:引入 u 的 2 阶微分,令 P = uxx, Q = uyy,方程变为:Pxx + Pyy + Qyy = f.
现在可以用 COMSOL Multiphysics 求解如下等价的 u, P, Q 的 PDEs。
Pxx + Pyy + Qyy = f
uxx = P
uyy = Q
这个方程组可以通过泛用型 PDE 应用模式来求解,因变量是 u, P, Q,模型方程系数为:
Gamma1 = (Px, Py+Qy), F1 = f
Gamma2 = (ux, 0), F2 = P
Gamma3 = (0, uy), F3 = Q
对于边界条件,按照如下情况处理:
a) 在边界上给定 u, uxx, 和 uyy,可以通过对 u, P, Q 使用 Dirichlet 边界条件来实现。
b) 在边界上给定 u 及其法向微分 du/dn。这表明 u 的切向微分也同样可以计算,因此在边界上已知 ux 和 uy 的表达式。这些边界条件可以通过对 u 使用 Dirichlet 边界条件以及对 P和 Q 使用 Neumann 边界条件来实现。
推文| 赵佳乐
审核| 小苏
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2025-07-05
最近编辑:1天前
相关推荐
最新文章
热门文章