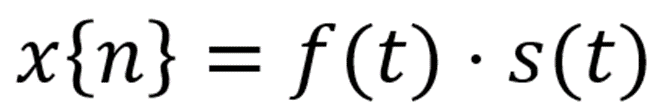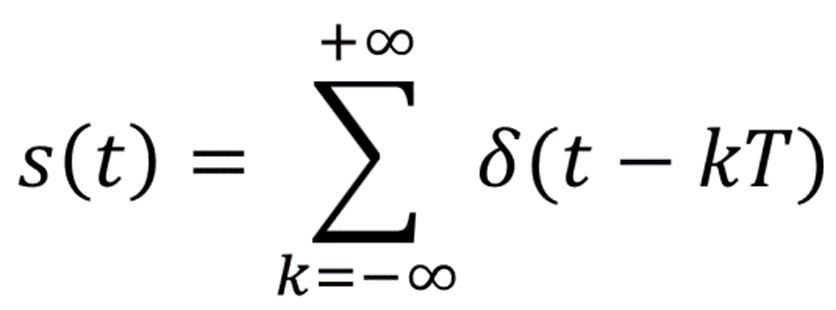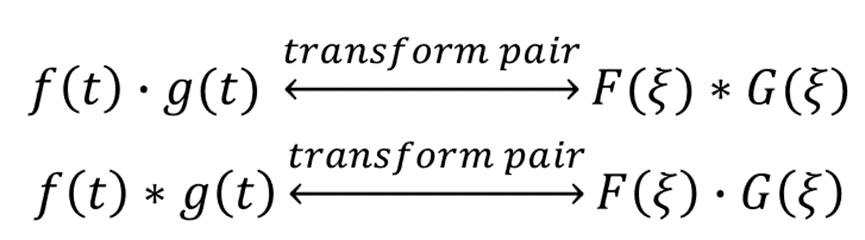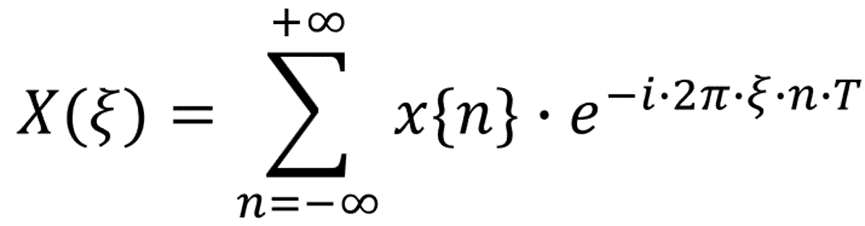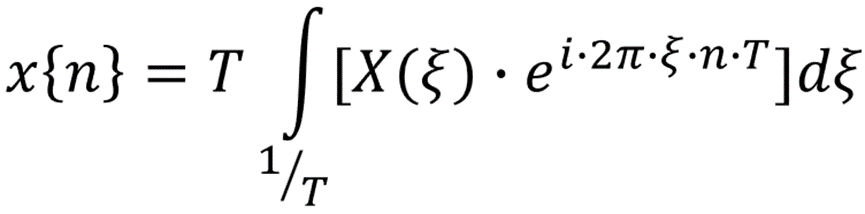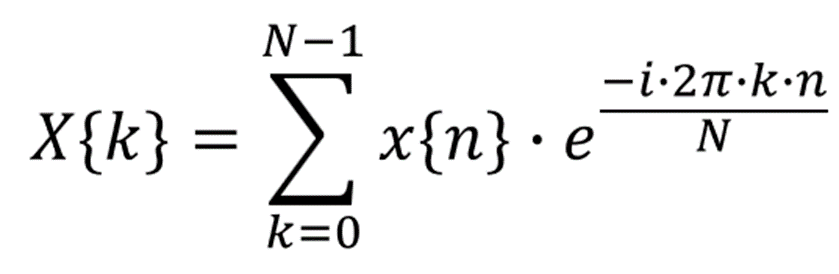傅里叶分析(2)
在《傅里叶分析(1)》中,讲述了连续信号的傅里叶分析方法,本文讲述离散信号的傅里叶分析方法。虽然电、声、光、机械振动等信号在物理上是连续函数,但在实际工程中,其通常为离散信号,即若干离散的数据点。对于离散信号,傅里叶级数和傅里叶变换已经无法使用,需要使用 DTFT(离散时间傅里叶变换)和 DFT(离散傅里叶变换)分析离散信号。1 离散信号的来源
离散信号来源于对连续信号的采样。数学处理上,离散信号为连续信号和采样函数(sampling function)的乘积: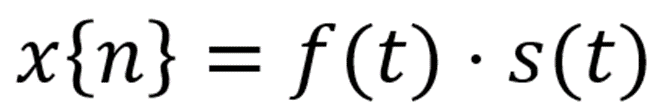
采样函数为基于狄拉克 δ 函数(Dirac delta function)表述的脉冲序列,其定义如下: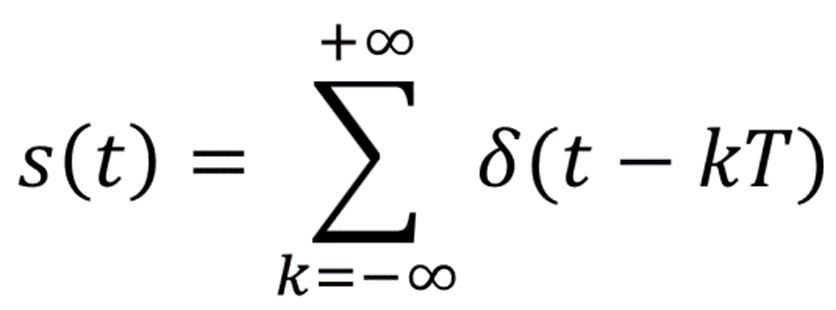
采样函数为周期函数,其在非采样时刻的函数值为 0,由此可得仅限采样时刻的离散数据点。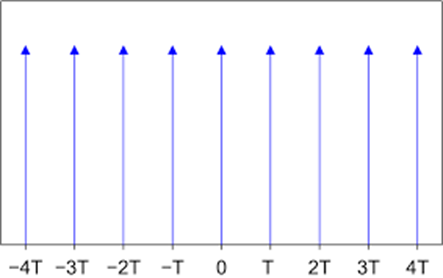
采样函数的图像(图源:维 基百科)
采样函数的傅里叶变换为频域上的采样函数,其周期为 1/T:
2 DTFT
根据前述采样方法,可将离散信号 x{n} 视为连续函数,除了采样点之外其他时刻函数值均为0。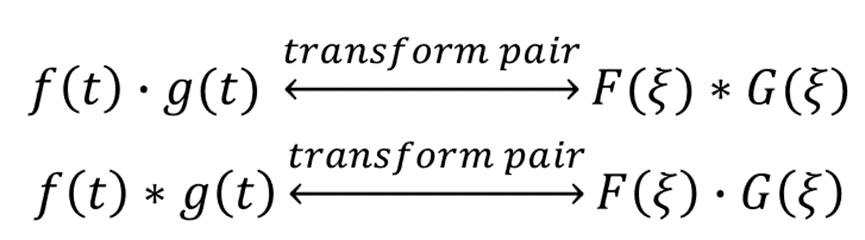
利用傅里叶变换的卷积特性,对 x{n} 进行傅里叶变换,其结果即 DTFT 计算公式为: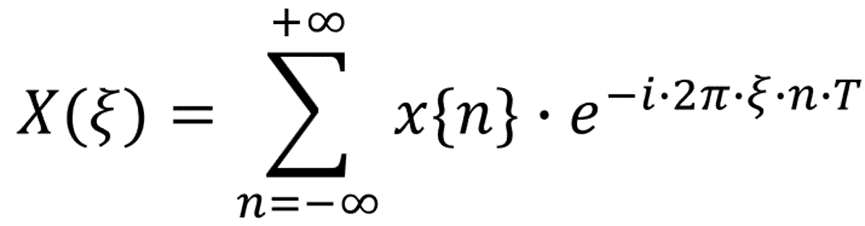
变换结果 X(ξ) 为连续周期函数,其周期为 1/T,即 X(ξ)=X(ξ+n/T)。由于 X(ξ) 为连续函数,其逆变换可直接使用傅里叶逆变换的计算公式。对于周期函数,可将积分区间从无穷大简化到一个周期内,得到 DTFT 逆变换公式: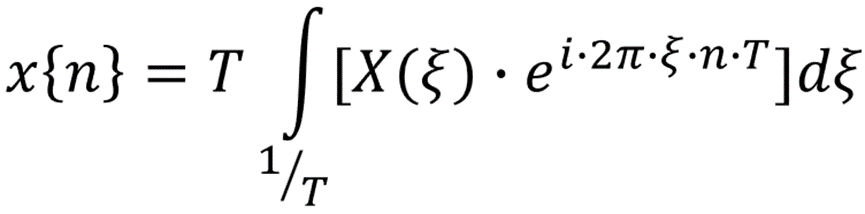
其中,积分区间可为任意的区间,只需满足区间的长度为单个周期长度 1/T 即可。根据 n 取值的不同即可获得 x{n} 各项取值。对于纯实数的信号 x{n},其变换结果X(ξ) 在正频率和负频率的幅值为对称关系。3 DFT
虽然 DTFT 表明了离散信号的频谱分析方法,但是得到的频谱是连续函数,对基于程序的实际信号分析造成很大困难。引用 DTFT 思路,将 x{n} 视为连续函数。根据连续信号的频谱特征,周期函数的频谱为离散点,由此可对频谱进行程序处理。将包含 N 个数据点的有限数据集 x{n}(从x{0} 至 x{N-1}),进行周期延拓,即 x{n} =x{n+k*T*N)},可使之成为在无穷大区间均有定义的周期函数,其周期为 T*N。由于 x{n} 的周期性,对 x{n} 进行DTFT 仅需在单周期内即可进行。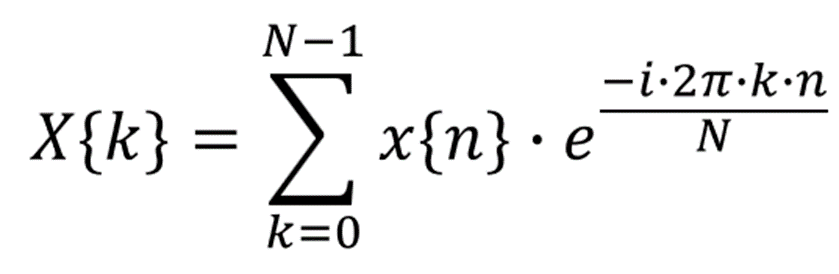
很显然,X{k} 在区间 [0, N-1] 只有N 个取值,且周期为 N。同理,在频域的单周期内进行 DTFT 逆变换,即可得到 DFT 逆变换计算公式:
对于纯实数的信号 x{n},其变换结果 X(ξ) 在正频率和负频率的幅值为对称关系。4 重要问题
4.1 频谱的类型
通常而言,时域信号 x{n} 来源为传感器信号、A/D电路转换等,其表示的物理量通常为可直接测量的物理量,如速度、电流、温度等。实际应用中,频谱通常分为幅值谱(amplitude spectrum)和功率谱(power spectrum)两类。幅值谱表示与功率的平方根成比例的物理量(如速度、电流、电压等);功率谱表示功率或与功率成比例的物理量(如光强度、声强度等)。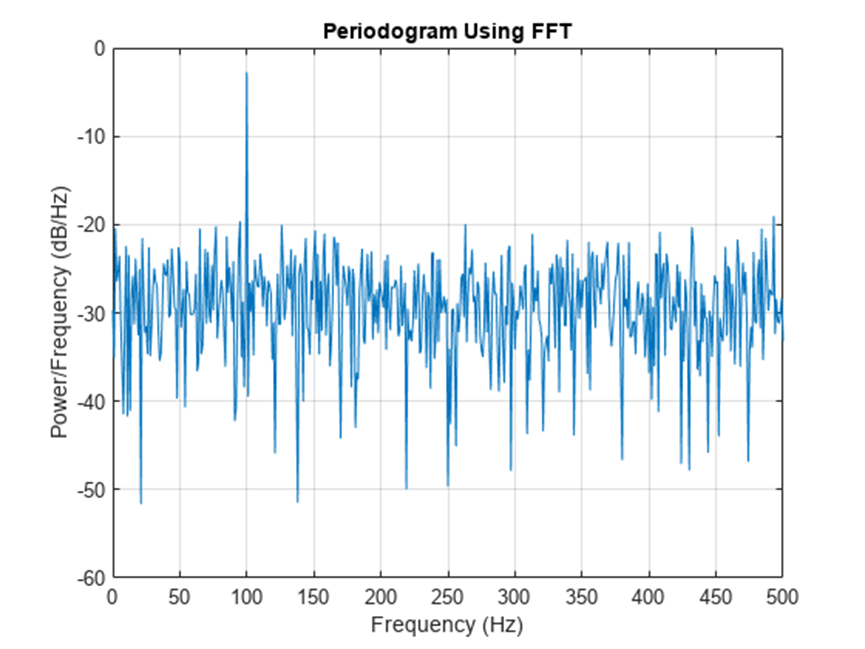
功率谱示意图(图源:mathworks.com)

4.2频谱范围与精度

根据奈奎斯特采样定理(Nyquist sampling theorem),离散信号可分析的频谱最高频率为采样频率的一半。对于更高频率部分,DFT 已无法分析。
其中 N 为信号的数据点数量。若需要更精细的频谱分辨率,只需要增加信号样本数量即可。4.2 数据处理与窗函数
对离散信号的周期延拓,通常会在信号首尾两端形成较大的不连续。信号在时域的不连续会导致频谱泄露(spectral leakage),即人为形成某些本不存在的谐波。通过窗函数(window function)对离散信号进行处理,使信号首尾两端的幅值逐步降低,可降低信号在两端的不连续性。通过窗函数处理后的信号 y{n} 和原始信号 x{n} 之间,满足:

窗函数应用效果对比(图源:《Digital Signal Processing Fundamentals and Applications》,作者 Li Tan)
常用的窗函数包括三角、Hamming、Hanning等。若信号是宽带信号,即不存在很明显的频域尖峰,可无需窗函数处理。Hanning 窗函数适用于多数常规问题,可作为通用的窗函数。
Hanning 窗函数特点为在信号首尾两端幅值为 0,正中心位置幅值为 1。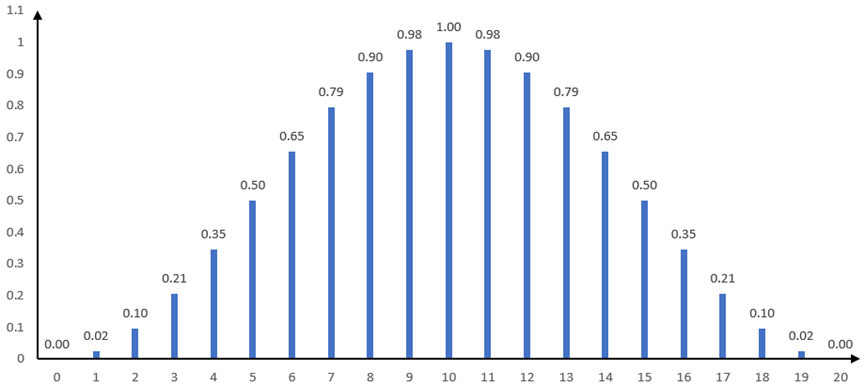
包含 21 个数据点的 Hanning 窗函数图像
5 DFT 和 FFT 的关系
快速傅里叶变换(Fast Fourier Transform,FFT)是 DFT 的一种计算方法。FFT 本质上是利用其它替代计算方式,避免根据 DFT 的定义直接计算 DFT,从而加快计算速度,节约硬件资源。FFT 当前最常用方法为 Cooley–Tukey 方法。许多工程计算软件均有 FFT 相关功能,直接导入数据序列进行分析即可。6 总结
对(1)、(2)文的重点进行总结:
傅里叶级数和傅里叶变换表述了连续信号频谱分析方法
DTFT 表述了无限多样本的离散信号频谱分析方法
DFT 表述了有限多样本的离散信号频谱分析方法
只有 DFT 可直接用于程序计算
使用 FFT 可加快 DFT 计算速度