粒子系统邻域搜索的快速矩阵计算方法

Fast matrix computing method of neighbor searching for particle systems

Wenqiang Xia^a, Chun Liu^a*, Yintong Min^a, Hanwen Li^a

Abstract: With the growing complexity of particle-based simulations, efficient neighbor searching algorithms are crucial for improving computing performance. Conventional neighbor searching algorithms are generally based on iterative or list-based operations, which face challenges in computational speed and complexity within high-performance computing. A novel neighbor searching algorithm based on pure matrix operations is proposed in this paper. In the algorithm, all the element properties (including coordinates, radii, stiffness, etc.) are stored in arrays. A neighbor matrix can be efficiently obtained via a series of pure matrix operations, such as substitution, sorting and arithmetic calculations. The indexes of neighboring elements are recorded rows by rows in the neighbor matrix. As the number of neighboring elements varies between rows, a virtual element is introduced to fill the spaces in the neighbor matrix. Numerical tests demonstrate the consistent superiority of the proposed pure matrix algorithm over a conventional linked-list method. Across the tested range of 200 to 2,000,000 elements, the matrix-based approach maintains significantly higher computational speeds, achieving its maximum performance advantage of approximately 13 times faster. As the algorithm and further computation of particle system are based on simple matrix operations, it is highly suitable for GPU computing and subsequent particle dynamics calculations. Overall, the neighbor searching algorithm developed in this study enables efficient simulations in particle system.

Keywords: Matrix computing; Neighbor searching; Discrete element method; GPU; MatDEM

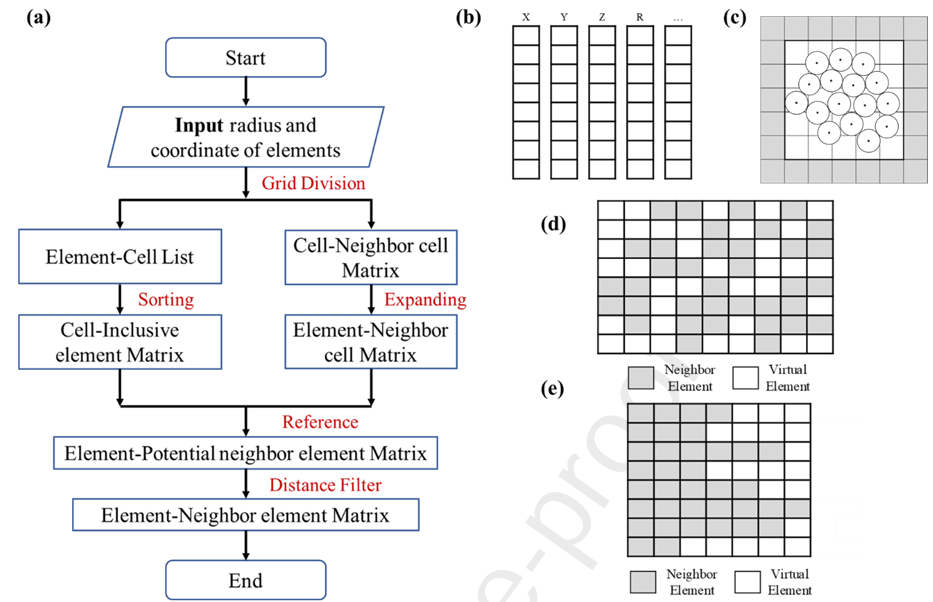
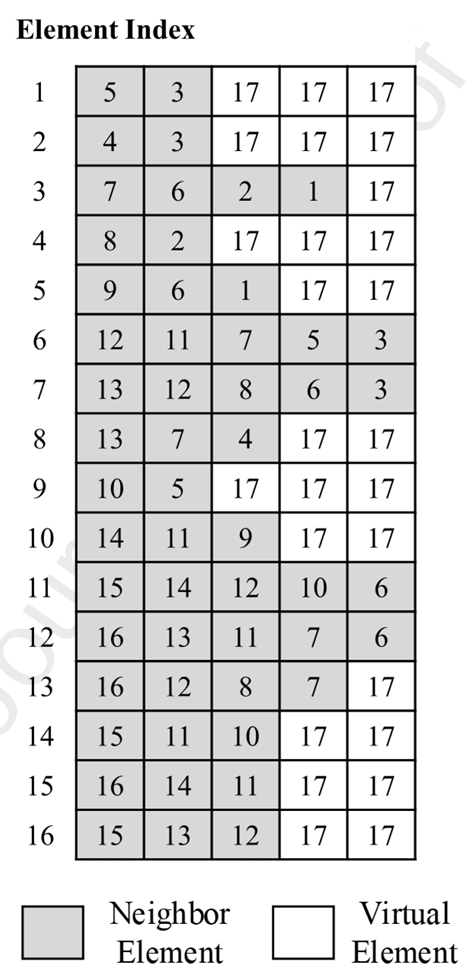
Fig.1 (a) Flow char of pure matrix neighbor searching algorithm; (b) Elements’ information list; (c) Schematic diagram of grid generation; (d) Application of virtual element; (e) Neighbor Matrix

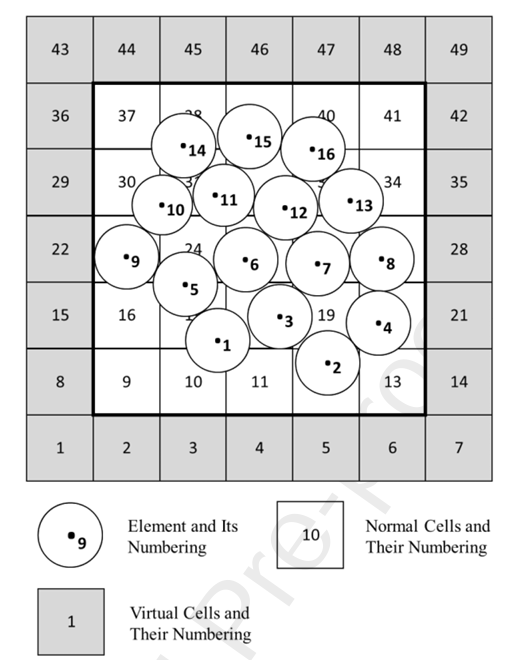
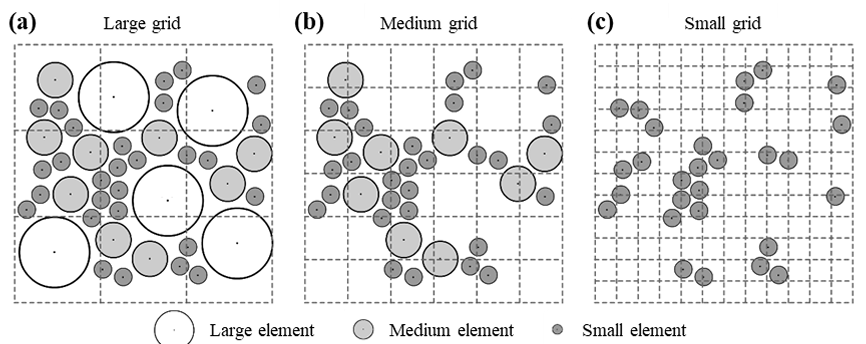
Fig.2 Spatial Discretization Strategy with Grid Cell Division, Virtual Boundary Layers, and Element Indexing

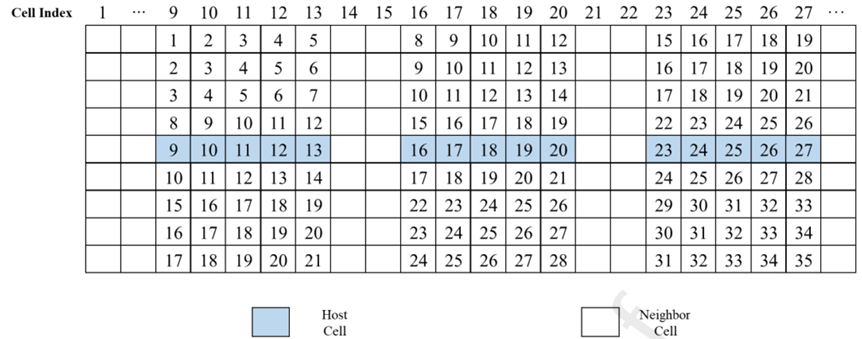
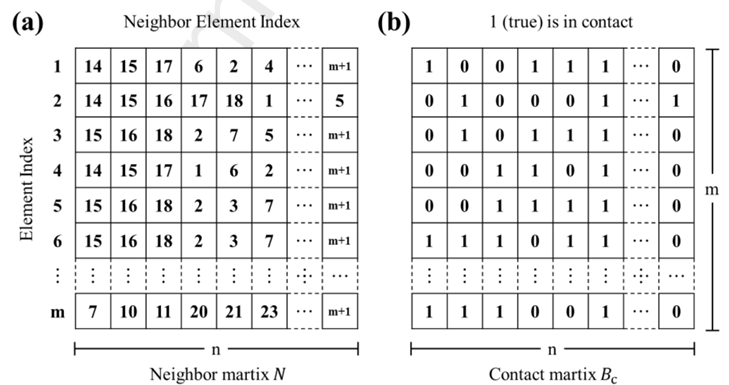
Fig.4 Cell-Neighbor Cell Matrix recording all neighbor cell indices

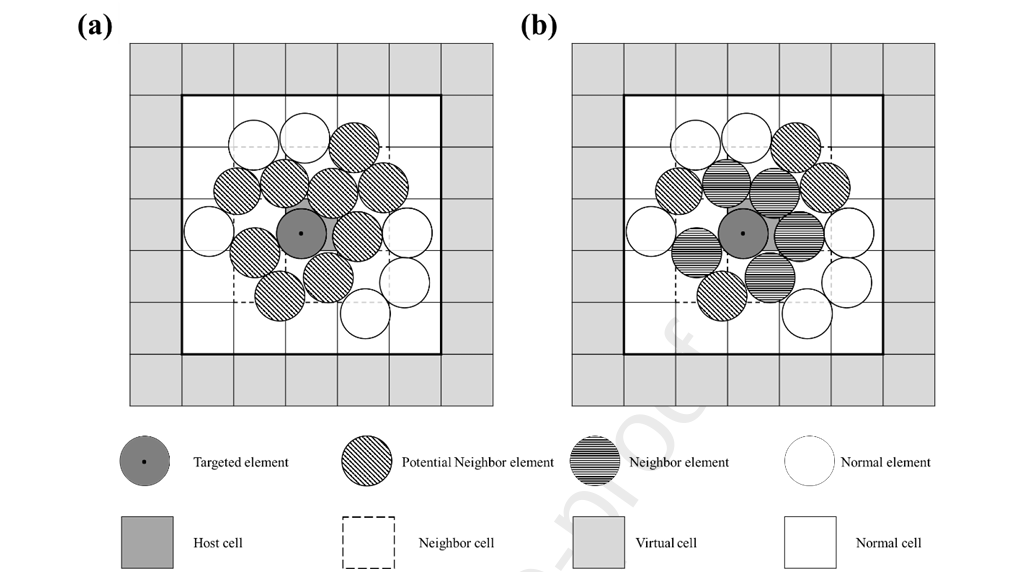
Fig.7 (a) Target element in the orthogonal grid and its potential neighbor elements; (b) Final neighbor element after distance filtering

Xia W, Liu C, Min Y, et al. Fast matrix computing method of neighbor searching for particle systems[J]. Powder Technology, 2025: 121807.