信号处理专题 | 旋转机械故障诊断的新分解理论——特征模态分解
特征模态分解(FMD)的用途是通过自适应FIR滤波器组与相关峭度目标函数,从含干扰和噪声的复杂信号中精准提取机械故障的周期性脉冲特征;其意义在于突破传统分解方法对滤波器参数的依赖及对故障特征考虑不足的局限,为旋转机械故障诊断提供更鲁棒、高效的信号分解工具,助力设备状态监测与运维优化。
目录
1 前言
在旋转机械故障诊断领域,特征提取是实现设备状态监测与故障定位的核心环节,传统信号分解方法在复杂工况下暴露出显著局限:EMD易受模态混叠与边界效应影响,EEMD、LMD等递归方法未充分考虑故障信号的本质特征;VMD需依赖人工调试模态数与平衡参数,且未聚焦故障信号特有的冲击性与周期性。
特征模态分解(FMD)正是为破解上述难题而提出,在理论层面,FMD实现了对故障信号冲击性与周期性的同步考量,无需故障周期先验知识即可实现故障特征的定向提取。在单一故障和多频段复合故障的特征提取中,均能从强干扰信号中分离出高信噪比的故障模态,其性能显著优于主流的VMD。
2 FMD的基本过程
FMD核心是从强干扰信号中精准提取含故障特征的模态。先准备一组“探测工具”(FIR滤波器组)全面扫描信号的所有频率区域,再通过反复调整工具的“探测方向”(迭代更新滤波器、估计故障周期),让工具精准锁定含故障特征的信号片段,最后剔除重复或无用的片段,留下最纯净的故障(特征模态)。
其基本过程可拆解为以下5个关键步骤:
2.1 输入参数与原始信号加载
此为FMD的启动环节,输入4类通用参数(无需故障相关先验信息)与原始振动信号,具体包括
(1)核心输入:采集的原始振动信号x(t)(含故障冲击、噪声、干扰等混合成分);
(2)预设参数:目标模态数n(匹配故障类型,单一故障设1,复合故障设2~3);FIR滤波器长度L(推荐30~100,对分解性能鲁棒性强);频段分段数K(推荐5~10,决定初始滤波器覆盖的子频段数量);最大迭代次数Imax(控制算法收敛效率)。
2.2 FIR滤波器组初始化:构建分解“候选池”
FMD通过汉宁窗设计初始化覆盖全频段的FIR滤波器组,为后续分解提供基础方向,避免盲目搜索。具体流程为: 频段均匀划分:根据采样频率,将信号全频段(0~ )均匀拆分为 个子频段,第 个子频段的上下截止频率为
为该频段的下截至频率、 为该频段上截至频率。
生成滤波器组:以汉宁窗为窗函数,针对每个子频段生成1个FIR滤波器,最终形成含 个滤波器的滤波器组。此环节的作用是将全频段离散为多个子区域,确保故障可能存在的任何频段都有对应的初始滤波器覆盖,为后续自适应优化奠定基础。
2.3 迭代优化:动态锁定故障特征(核心环节)
该环节是FMD实现“自适应”的关键,通过“模态生成→周期估计→滤波器更新”的循环迭代,逐步将滤波器“聚焦”到故障特征频段,具体步骤为
(1)模态生成:将原始信号x(t)与当前第k个滤波器系数 进行卷积运算,得到第i次迭代的候选模态 (卷积本质是加权求和,提取对应频段成分)。每个滤波器对应一个初始子频段(例如1000–2000Hz),卷积运算会保留原始信号中该频段的成分,过滤掉其他频段的干扰,生成的 就是该滤波器“认为可能含故障”的候选信号片段。
(2)故障周期估计:计算候选模态 的自相关函数 ,找出自相关谱“过零点后第一个局部最大值”对应的延迟值 ,将其作为当前故障周期估计值 。
故障的核心特征是“周期性冲击”(如轴承外圈缺陷每旋转一周冲击一次),体现在自相关谱上就是“出现局部最大值”。第一个局部峰值 对应的就是最可能的故障周期。第一轮迭代的 可能不够准(因候选模态含干扰),但随着滤波器优化,候选模态中故障成分越来越纯,后续迭代的 会逐渐收敛到真实故障周期。
(3)滤波器系数更新:相关峰度(CK)最大化为目标,通过求解广义特征值问题更新滤波器系数 为 。
以相关峰度(CK)为目标函数(同步衡量信号冲击性与周期性,故障成分CK值显著高于干扰,参考论文[1]),通过求解广义特征值问题,优化滤波器系数至,使新滤波器更易提取高CK值的故障成分; FMD的目标就是让更新后的滤波器提取的模态 具有最大CK值,CK公式为
为加权相关矩阵,与估计的周期 相关; 为共轭转置。
将模态 (X为信号矩阵, 为滤波器系数向量)带入CK.
为加权相关矩阵, 为信号相关矩阵。 数学上,最大化该比值等价于求解以下广义特征值问题:
其中, 与最大特征值 对应的特征向量,就是更新后的最优滤波器系数 。
(4)迭代终止判断:重复上述步骤,直至迭代次数达到 ,此时滤波器组已自适应向故障频段收敛。迭代过程中,故障周期估计与滤波器更新形成闭环反馈:滤波器优化使模态更接近故障特征,而更纯净的模态又能提升周期估计精度,最终实现“滤波器-周期-模态”的协同收敛。
2.4模态选择:剔除冗余与混叠,提纯故障模态
由于初始滤波器组覆盖全频段,迭代后可能产生冗余模态(含重复故障成分)或混叠模态(故障与干扰共存),需通过模态选择机制提纯
(1)冗余识别:计算所有候选模态间的相关系数(CC)矩阵——CC接近的两模态高度相似,存在冗余或混叠;
(2)故障模态筛选:对CC最大的冗余模态对,保留CK值更高的模态(CK高意味着故障特征更纯净),剔除CK值低的干扰模态;
(3)循环筛选:重复上述步骤,直至剩余模态数等于预设目标数n,最终得到仅含核心故障特征的模态。该环节通过“CC去冗余+CK保故障”的双重逻辑,解决了传统分解方法“模态混叠、冗余量大”的痛点。
2.5输出故障特征模态
最终输出经筛选后的n个故障特征模态,这些模态具有高信噪比、故障特征清晰的特点
(1)时域上可见明显的故障周期性冲击;
(2)频域(包络谱)上可清晰观察到故障特征频率及其倍频、边频带。如图1(a)、图1(b),可直接用于后续故障类型定位(如内圈/外圈故障)。

3 实验台及数据集描述
采用凯斯西储大学轴承数据集中12k驱动端轴承故障数据,数据为.mat数据,包含三类数据振动信号,分别为0马力0.007”内圈故障、0马力0.007”滚动体故障、0马力0.007”外圈故障的振动片段。
3.1 特征频率计算
轴承故障特征频率是通过轴承几何参数和运行转速计算得出的特定频率,是振动分析诊断轴承故障的核心依据。不同部件(内圈、外圈、滚动体)的故障会激发对应频率的振动信号,准确识别这些频率可快速定位故障类型。计算分析故障轴承的特征频率如表1所示。
表1 特征频率
故障类型 | 特征频率 |
内圈故障 | 162.18 Hz |
滚动体故障 | 70.60 Hz |
外圈故障 | 107.33 Hz |
3.2 FMD结果
(1) 0马力0.007”内圈故障
图例:原始信号及其分解模特包络谱图
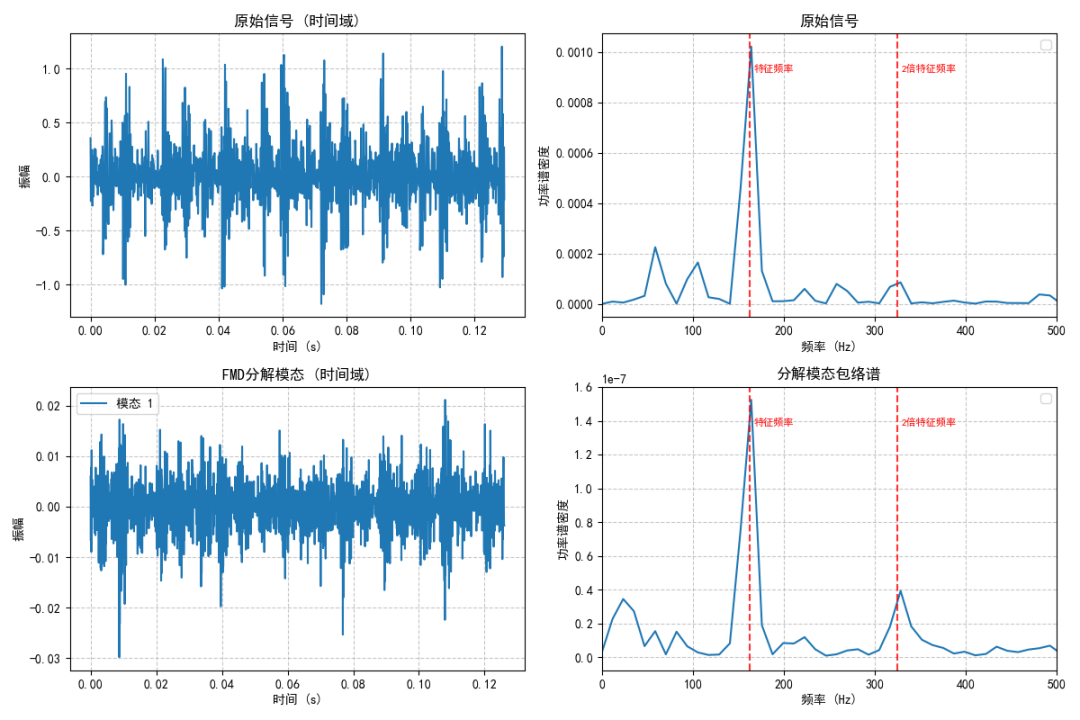
(2) 0马力0.007”滚动体故障
图例:原始信号及其分解模特包络谱图
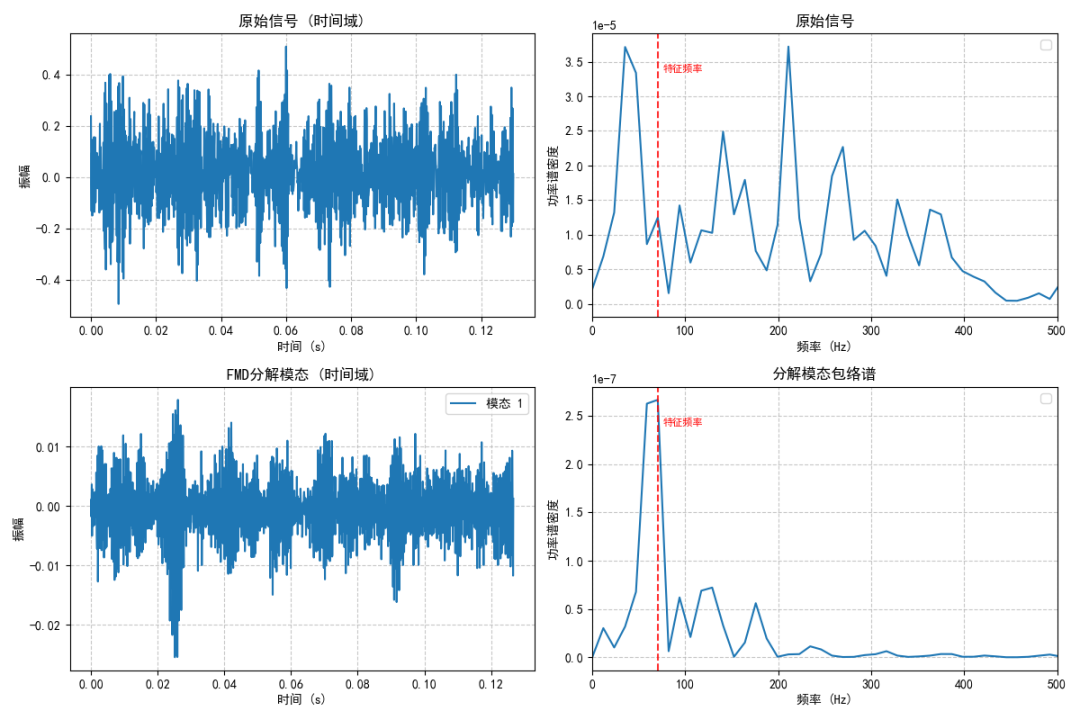
(3) 0马力0.007”外圈故障
图例:原始信号及其分解模特包络谱图
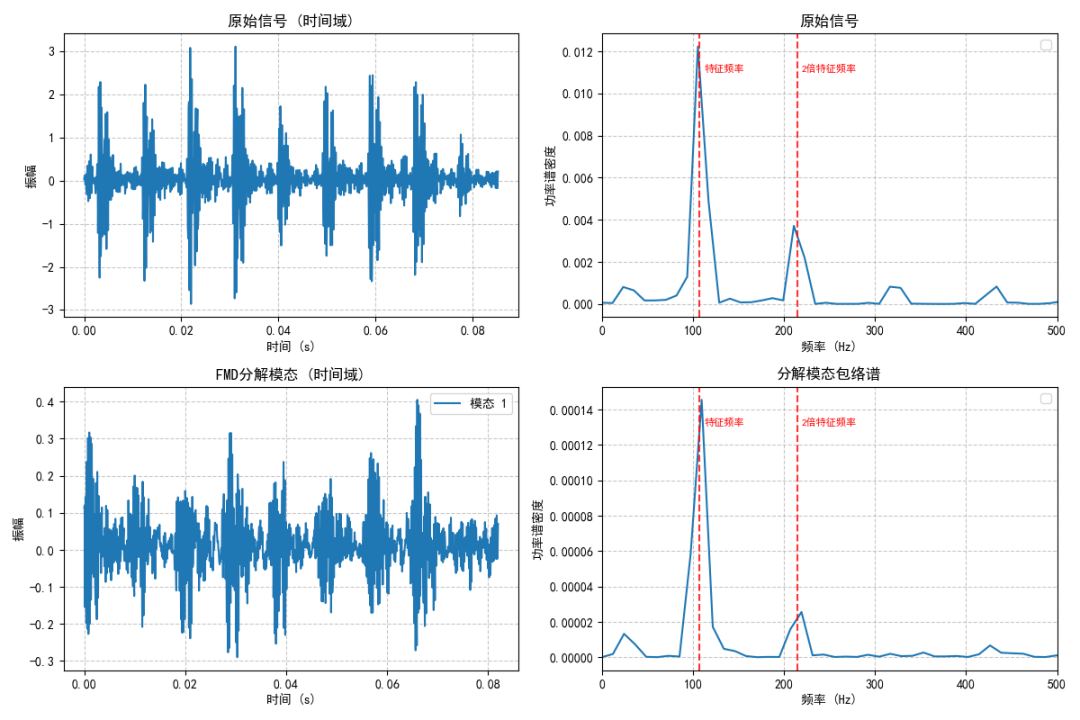
3.3 结果分析
凯斯西储大学故障数据集本身具备较为显著的特征,因此直接对原始信号进行包络谱分析时,针对内圈故障与外圈故障,仍可获得准确度较高的诊断结果。不过,若对滚动体故障信号直接应用包络谱分析,则难以实现精准的故障诊断。
上述三类故障数据先采用 FMD进行处理,再开展包络谱分析时,均能稳定输出准确的故障诊断结果。需要说明的是,该数据集仅包含单一故障类型,若需拓展至复合故障诊断场景,通过调节 FMD 的分解模态个数即可满足诊断需求。
3.4 代码
import numpy as npimport scipy.signal as signalfrom scipy.linalg import eigimport matplotlib.pyplot as pltfrom matplotlib.gridspec import GridSpecfrom scipy.io import loadmat# 设置中文字体plt.rcParams["font.family"] = ["SimHei"]plt.rcParams["axes.unicode_minus"] = Falsedef init_fir_bank(K, L, fs):"""初始化汉宁窗FIR滤波器组"""fir_bank = []nyquist = fs / 2freq_bands = np.linspace(0.01 * nyquist, 0.99 * nyquist, K + 1)for k in range(K):f_l = freq_bands[k]f_u = freq_bands[k + 1]if f_l <= 0:f_l = 0.001 * nyquistif f_u >= nyquist:f_u = 0.999 * nyquisttaps = signal.firwin(L, [f_l, f_u], fs=fs,pass_zero=False, window='hann')fir_bank.append(taps)return np.array(fir_bank)def calc_ck(u, Ts, M=1):"""计算相关峭度(CK)"""N = len(u)if Ts <= 0 or Ts >= N // 2:return 0.0valid_idx = np.arange(Ts, N)numerator = np.sum((u[valid_idx] * u[valid_idx - Ts]) ** 2)denominator = (np.sum(u ** 2)) ** (M + 1)if denominator < 1e-12:return 0.0return numerator / denominatordef estimate_period(u, fs):"""基于自相关谱估计周期"""corr = np.correlate(u, u, mode='full')corr = corr[len(corr) // 2:]zero_cross_idx = np.where(corr < 0)[0]if len(zero_cross_idx) == 0:return int(fs / 30)zero_cross_idx = zero_cross_idx[0]post_corr = corr[zero_cross_idx:]peaks, _ = signal.find_peaks(post_corr)if len(peaks) == 0:return int(fs / 30)Ts = zero_cross_idx + peaks[0]return Ts if Ts < len(u) // 2 else int(fs / 30)def update_filter(x, u_prev, Ts, L):"""基于广义特征值求解更新FIR滤波器"""N = len(x)M_mode = len(u_prev)if M_mode < L:return np.zeros(L)X = np.zeros((M_mode, L))for i in range(M_mode):X[i, :] = x[i:i + L]W = np.zeros(M_mode)valid_idx = np.arange(Ts, M_mode)W[valid_idx] = (u_prev[valid_idx] * u_prev[valid_idx - Ts]) ** 2sum_u_sq = np.sum(u_prev ** 2)W = W / sum_u_sq if sum_u_sq > 1e-12 else WW_diag = np.diag(W)R_XWX = X.T @ W_diag @ XR_XX = X.T @ Xtry:eig_vals, eig_vecs = eig(R_XWX, R_XX)eig_vals_real = np.real(eig_vals)max_eig_idx = np.argmax(eig_vals_real)optimal_filter = np.real(eig_vecs[:, max_eig_idx])optimal_filter = optimal_filter / np.linalg.norm(optimal_filter)except:optimal_filter = np.zeros(L)optimal_filter[0] = 1.0return optimal_filterdef calc_cc(u1, u2):"""计算两模态的相关系数(CC)"""u1_mean = np.mean(u1)u2_mean = np.mean(u2)numerator = np.sum((u1 - u1_mean) * (u2 - u2_mean))denom1 = np.sqrt(np.sum((u1 - u1_mean) ** 2))denom2 = np.sqrt(np.sum((u2 - u2_mean) ** 2))if denom1 < 1e-12 or denom2 < 1e-12:return 0.0return numerator / (denom1 * denom2)def select_modes(modes, K_init, n_target, fs):"""模态选择"""current_modes = modes.copy()current_K = K_initwhile current_K > n_target:cc_matrix = np.zeros((current_K, current_K))for i in range(current_K):for j in range(i + 1, current_K):cc = calc_cc(current_modes[i], current_modes[j])cc_matrix[i, j] = cccc_matrix[j, i] = ccmax_cc = -1.0max_pair = (0, 1)for i in range(current_K):for j in range(i + 1, current_K):if cc_matrix[i, j] > max_cc:max_cc = cc_matrix[i, j]max_pair = (i, j)i, j = max_pairTs_i = estimate_period(current_modes[i], fs)Ts_j = estimate_period(current_modes[j], fs)ck_i = calc_ck(current_modes[i], Ts_i)ck_j = calc_ck(current_modes[j], Ts_j)if ck_i >= ck_j:current_modes = np.delete(current_modes, j, axis=0)else:current_modes = np.delete(current_modes, i, axis=0)current_K -= 1return current_modesdef plot_envelope_spectrum(sig, fs, ax, title, xlim=None, vert_dashes=None, dash_labels=None):"""绘制包络谱"""ana lytic_signal = signal.hilbert(sig)envelope = np.abs(an alytic_signal)f, Pxx = signal.welch(envelope, fs, nperseg=1024)ax.plot(f, Pxx)ax.set_title(title)ax.set_xlabel('频率 (Hz)')ax.set_ylabel('功率谱密度')ax.grid(True, linestyle='--', alpha=0.7)if xlim:ax.set_xlim(xlim)# 添加带文字的竖直虚线if vert_dashes is not None and dash_labels is not None:for dash, label in zip(vert_dashes, dash_labels):ax.axvline(x=dash, color='r', linestyle='--', alpha=0.8)# 在虚线右侧添加文字标注,y坐标取功率谱密度的最大值附近max_p = np.max(Pxx)ax.text(dash + 5, max_p * 0.9, label, color='r', fontsize=8)def plot_filter_response(filters, fs, ax, title):"""绘制滤波器频率响应"""for i, filt in enumerate(filters):w, h = signal.freqz(filt, fs=fs)ax.plot(w, 20 * np.log10(np.abs(h)), label=f'滤波器 {i+1}')ax.set_title(title)ax.set_xlabel('频率 (Hz)')ax.set_ylabel('幅度 (dB)')ax.grid(True, linestyle='--', alpha=0.7)ax.legend(fontsize='s mall')ax.set_xlim(0, fs/2)ax.set_ylim(-60, 10)def feature_mode_decomposition(x, fs, n_target=1, K=8, L=40, max_iter=5, plot_results=True, vert_dashes=None, dash_labels=None):"""特征模态分解(FMD)主函数"""if x.ndim > 1:x = x.flatten() # 将多维数组展平为一维# 1: 初始化FIR滤波器组fir_bank = init_fir_bank(K=K, L=L, fs=fs)# 2: 初始滤波生成模态M_mode = len(x) - L + 1modes = np.zeros((K, M_mode))for k in range(K):modes[k] = signal.convolve(x, fir_bank[k], mode='valid')# 保存初始滤波器用于可视化initial_filters = fir_bank.copy()# 3: 迭代更新滤波器与模态for iter_idx in range(max_iter):updated_fir = []updated_modes = []for k in range(K):Ts = estimate_period(modes[k], fs)new_filter = update_filter(x, modes[k], Ts, L)updated_fir.append(new_filter)new_mode = signal.convolve(x, new_filter, mode='valid')updated_modes.append(new_mode)fir_bank = np.array(updated_fir)modes = np.array(updated_modes)# 4: 模态选择final_modes = select_modes(modes=modes, K_init=K,n_target=n_target, fs=fs)# 可视化结果if plot_results:t = np.linspace(0, len(x)/fs, len(x), endpoint=False)t_mode = np.linspace(0, M_mode/fs, M_mode, endpoint=False)# 创建图形(调整网格布局,仅保留4个子图)fig = plt.figure(figsize=(12, 8))gs = GridSpec(2, 2, figure=fig)# 1. 原始信号时间波形ax1 = fig.add_subplot(gs[0, 0])ax1.plot(t[:len(t)], x[:len(t)])ax1.set_xlabel('时间 (s)')ax1.set_ylabel('振幅')ax1.grid(True, linestyle='--', alpha=0.7)# 2. 原始信号包络谱(添加带文字的竖直虚线)ax2 = fig.add_subplot(gs[0, 1])plot_envelope_spectrum(x, fs, ax2, '原始信号', xlim=(0, 500), vert_dashes=vert_dashes, dash_labels=dash_labels)ax2.legend() # 显示图例# 3. 最终分解模态时间波形ax3 = fig.add_subplot(gs[1, 0])for i, mode in enumerate(final_modes):ax3.plot(t_mode[:len(t_mode)], mode[:len(t_mode)], label=f'模态 {i+1}')ax3.set_title('FMD分解模态 (时间域)')ax3.set_xlabel('时间 (s)')ax3.set_ylabel('振幅')ax3.grid(True, linestyle='--', alpha=0.7)ax3.legend()# 4. 最终分解模态包络谱ax4 = fig.add_subplot(gs[1, 1])for i, mode in enumerate(final_modes):plot_envelope_spectrum(mode, fs, ax4, f'模态 {i+1}', xlim=(0, 500), vert_dashes=vert_dashes, dash_labels=dash_labels)ax4.set_title('分解模态包络谱')ax4.legend()plt.tight_layout()plt.show()return final_modes, M_mode# 调用if __name__ == "__main__":# 加载MAT文件数据data4 = loadmat(".mat") # 加载mat文件data_list4 = data4["X118_DE_time"].flatten()x = data_list4[2040:3600] # 取x个数据点fs = 12000 # 设置采样频率# 定义要添加的竖直虚线横坐标和对应文字vert_dashes = [xxx]dash_labels = ["特征频率"]# 执行FMD分解(传递vert_dashes和dash_labels参数)final_modes, mode_length = feature_mode_decomposition(x=x, fs=fs, n_target=1, K=4, L=40, max_iter=5, plot_results=True,vert_dashes=vert_dashes, dash_labels=dash_labels)# 输出结果信息print(f"FMD分解完成!")print(f"原始信号长度: {len(x)} 采样点")print(f"分解模态长度: {mode_length} 采样点")print(f"保留模态数量: {len(final_modes)} 个")
4 总结
FMD的基本过程本质是“从粗到精”的自适应聚焦过程:
(1)以汉宁窗滤波器组初始化实现“全频段覆盖”(粗筛);
(2)以“周期估计+CK优化”的迭代实现“故障频段聚焦”(精调);
(3)以“CC+CK”的模态选择实现“故障特征提纯”(终筛)。
整个过程无需故障周期、频率等先验知识,通过信号自身特征动态优化,对强干扰、低信噪比及复合故障场景均具有强适应性,是其区别于VMD等传统方法的核心优势。
5 参考文献
[1] YONGHAO MIAO, BOYAO ZHANG, CHENHUI LI, et al. Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis[J]. IEEE Transactions on Industrial Electronics,2023,70(2):1949-1960.
编辑:You
校核:李正平、陈凯歌、曹希铭、赵栓栓、赵学功、白亮、任超、Tina、陈宇航、海洋、陈莹洁、王金、赵诚、肖鑫鑫
该文资料搜集自网络,仅用作学术分享,不做商业用途,若侵权,后台联系小编进行删除





