动态力学分析 (DMA) 基础知识
动态力学分析 (DMA) 是一种表征方法,可用于研究材料在各种条件下(例如温度、频率、时间等)的动态行为。DMA 测试是一门研究从液体到固体的各种材料的粘弹性的学科。本文将讨论 DMA 的基本原理、基础知识、不同的测量模式和测量系统。
一. 什么是 DMA?
在 DMA 测量中,我们分析的是固体样品的粘弹性材料随时间和温度变化的变形或流动特性,需要将样品置于一定的正弦应力(或应变)下,并测量材料的响应。
| DMA 测量的重要术语和变量: | ||
| 拉伸 | 旋转/剪切 | |
| 模量 | ||
| 复数模量 | E* | G* |
| 储能模量 | E' | G' |
| 损耗模量 | E'' | G'' |
| 损耗因子 | ||
| 应变 | ε | γ |
| 应力 | σ | τ |
| 角频率 | ω | ω |
| 时间 | ||
二. DMA 能告诉我们什么?
在 DMA 测量中,可以分析材料的粘弹性特性。主要输出值包括储能模量 E'和损耗模量 E''以及损耗或阻尼因子 tanδ。根据测试设置,可以描述多种不同的材料特性,例如物理特性(玻璃化转变温度 T g 、分子运动、结晶、固化/交联等)、力学特性(静态和动态模量、阻尼行为、蠕变和松弛行为等)以及长期材料行为(时间温度叠加(TTS))。
复数模量 |E*| – MPa
应力与应变振幅 σ A 和 ε A 之比;描述材料的刚度
储能模量 E' – MPa
测量负载阶段的储存能量
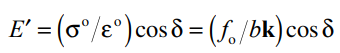
损耗模量 E'' – MPa
测量负载阶段由于内部摩擦而产生的(不可逆)耗散能量。
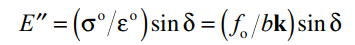
损耗因子 tanδ – 无量纲
E'' 和 E' 的比率;值是衡量材料阻尼行为的标准。
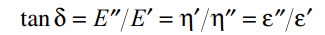
三. DMA 如何工作?
待测材料样品受到一定的正弦应力或应变(轴向或扭转变形)作用,并测量其反应(图 1)。理想弹性材料会立即做出反应,没有任何延迟,正弦应力和应变曲线没有相移,因此δ为零。理想粘性材料的应力和应变曲线显示相移角δ = 90°。正如“粘弹性”一词所暗示的,粘弹性材料的行为是两者的混合。因此,相移角为 0° < δ < 90°。

重要术语及其数学定义:

常见的 DMA 测量
除了由 DMA 仪器的线性或旋转驱动给出的机械应力幅度和频率的变化之外,还可以通过环境测试室设置温度或相对湿度等环境参数。
幅值扫描(AS)
振幅扫描测量用于确定材料的线性粘弹性 (LVE) 范围。此时主要发生弹性(可逆)变形,这与所有类型的 DMA 分析都密切相关,因为它能够在不破坏样品结构的情况下测量正确的绝对值。
振幅扫描试验在恒定的温度和频率下进行,仅施加的应变振幅在一定范围内变化。图 3 展示了振幅扫描的典型曲线。储能模量和损耗模量随变形的变化曲线在 LVE 范围内的低应变(平台值)下呈现恒定值。意味着粘弹性测试时施加的应变应在此范围内。

频率扫描(FS)
频率扫描通常提供无损变形范围内材料随时间变化的行为信息。试验过程中,频率会发生变化,而温度和施加的应变或应力保持不变。如有必要,应变可以在低能量损失 (LVE) 范围内变化。频率扫描通常与温度扫描结合使用,以生成用于时间温度叠加 (TTS) 的主曲线。

温度扫描(TS)
采用温度扫描进行可以确定样品的转变温度Tg(区域)。对于聚合物而言,玻璃化转变温度(Tg)尤为重要。测定 Tg 的不同方法将在以后章节中讨论。
包括温度变化在内的测量通常在恒定频率(例如 1 Hz)和恒定应力或应变下进行。在 LVE 范围内,施加的应变可能会发生变化。
湿度扫描
环境相对湿度也可能对样品的机械性能产生重大影响。这些测试通常在恒定温度和频率下进行。对于某些样品,为了提高测量曲线的准确性,改变变形模式是有意义的。然而,保持在 LVE 范围内至关重要。
时间扫描
在此类测试中,温度和频率保持恒定,并研究材料随时间的变化行为。例如,它用于研究树脂的固化反应。在这些测试中,可以分析材料从液态到固态的变化行为。由于液态和固态样品的材料特性差异很大,因此变形的变化(在 LVE 范围内)有助于提高测量精度。
热转变
使用 DMA 设备,可以根据包含温度梯度的测试规范测定热转变温度。这些转变温度对于聚合物尤其重要,因为它们的刚度在特定温度下会发生显著变化。为了针对特定应用选择合适的材料,了解聚合物的温度相关材料行为至关重要。图 5 显示了典型非晶态热塑性聚合物的温度依赖性行为。

如图所示,转变实际上并非发生在某个特定的温度下,而是在材料属性发生变化的某个温度范围内。因此,有多种方法可以确定玻璃化转变温度:
tanδ曲线的峰值
E''曲线的峰值
E'曲线上的阶梯法
E'曲线拐点法
所有这些方法各有利弊,结果也略有不同。因此,在比较不同材料时,使用相同的方法非常重要。还必须记住,转变温度是转变温度区域,而不是截然不同的确定值。
四. DMA 操作模式
由于 DMA 系统可以分析各种不同的材料,因此需要不同的测量系统和不同类型的负载。
负载类型
拉伸
弯曲
扭转/剪切
压缩
对于拉伸、弯曲和压缩的 DMA 测试,可以使用配备线性驱动器的经典独立 DMA 系统。此时,样品会受到轴向力。对于扭转或剪切的测量,则需要旋转驱动器。
请注意:不同类型的载荷(轴向力或旋转载荷)会导致不同的模量。杨氏模量或拉伸模量(也称为弹性模量,简称 E 模量)是使用轴向力测量的,而剪切模量(G 模量)是在扭转和剪切作用下测量的。由于 DMA 测量是在振荡条件下进行的,因此测得的值为复模量 E* 和 G*。对于各向同性材料,这两个值通过泊松比 ν: G∗=E∗2(1+ν) 联系起来。
这意味着,如果已知被分析材料的泊松比,就可以将一种测试的结果转换为另一种测试的结果。另一方面,如果可以测量材料的 G*和 E*,也可以确定泊松比。
请注意:由于 E 和 E*(静态与动态)的测定方法不同,同一种材料的数值并不相同。通常情况下,复数模量的值高于静态值。
测量系统
如上所述,可以使用 DMA 系统测试的材料范围非常广泛:从极低模量材料(例如非常柔软的低重量聚合物泡沫,约 0.01 至 0.1 MPa),到弹性体和热塑性塑料(约 0.1 至 50,000 MPa),以及纤维增强聚合物(约 10,000 至 300,000 MPa)。为了分析这些截然不同的材料类型,需要不同的测量系统:
表 1:DMA 测量系统概述、相应的变形模式以及适用样品的示例
| PP(平行板) | 泡沫 | ||||
| SRF(实心矩形夹具) | 热塑性塑料 | ||||
| SCF(实心圆形夹具) | 热塑性塑料 | ||||
| UXF(通用拉伸夹具) | 聚合物薄膜 | ||||
| TPB(三点弯曲) | 陶瓷 | ||||
| CTL(悬臂弯曲) | 弹性体 |
根据动态力学分析得出的特性选择材料
图 6 概述了损耗模量 tanδ和杨氏模量。它们是通过对不同材料和材料类别在 30°C 温度下进行动态力学分析推导出的。

表 2:图表中术语的缩写
| 缩写 | 完整术语 |
| IR | 异戊二烯 |
| VLD | 密度极低 |
| elPu | 聚氨酯弹性体 |
| MD | 中等密度 |
| LD | 低密度 |
| EVA | 乙烯-醋酸乙烯酯 |
| HD | 高密度 |
| PTFE | 聚四氟乙烯(特氟龙) |
| PE | 聚乙烯 |
| PP | 聚丙烯 |
| ABS | 丙烯腈丁二烯苯乙烯 |
| PMMA | 聚甲基丙烯酸甲酯 |
| GFRP | 玻璃纤维增强聚合物 |
| CFRP | 碳纤维增强聚合物 |
| Mg | 镁 |
| Ti | 钛 |
| WC | 碳化钨 |
| SiC | 碳化硅 |
| Si3N4 | 氮化硅 |
| Cu | 铜 |
| Al | 铝 |
上图这些材料涵盖不同的材料类别,例如金属、陶瓷材料、塑料等。例如,该图显示,工业陶瓷的模量非常高,但几乎没有阻尼能力。对于需要兼具高抗变形能力和中等阻尼能力的应用,金属材料或聚合物复合材料更适合,如图所示。相反,如果良好的阻尼性能在应用中至关重要,但机械承载能力却可以忽略不计,那么聚合物泡沫材料则是正确的选择。
这样,产品设计师可以一目了然地了解哪种材料类别符合特定应用的要求,从而预先选择合适的材料。对于想要更仔细地研究材料的材料科学家来说,该图表可以估算预期的力学性能。这在选择合适的测量系统和制定测试规范时非常有用。
来源:ABAQUS仿真世界





