CFD 博客 | 探索湍流中的非线性连续关系
本文翻译转载于:Cadence Blog
作者:Gaurav
要点
要点
●
湍流是一种普遍存在的现象,存在于从微观到宏观尺度的众多尺度流动中。
●
它涉及混乱、不规则的流体运动,通常以涡旋和涡流等旋转结构为特征。
●
湍流会显著影响气动阻力,并导致流体系统的能量耗散。
为何研究湍流?
为何研究湍流?
流体流动中的湍流行为是经典物理学中最令人关注且最具挑战性的问题之一。大多数流体流动都表现出湍流,湍流在已知宇宙的广泛尺度上发挥着关键作用。其影响范围广泛,从细胞内的微观生物过程和生物体的循环系统,到技术设备和家用电器。此外,湍流也存在于广泛的地球物理和天体物理现象中,包括行星内部、海洋、大气和恒星动力学,甚至延伸到星系和星系际尺度。
在整个 19 世纪和 20 世纪,许多杰出的物理学家和工程师致力于揭示湍流的奥秘。尽管湍流无处不在,但理解其潜在机制并准确预测其行为——即使在简单的场景中——仍然是经典物理学中尚未解决的重大问题之一。湍流研究的动机既在于其固有的机理复杂性,也在于其在科学和工程领域的潜在实际效益。
什么是湍流?
什么是湍流?
湍流是一种复杂的三维非稳定现象,常见于流体流动中,其特征是混沌和不规则的运动。与层流(流体微团沿平滑有序路径的运动)不同,湍流的速度、压力和其他流动特性会发生快速波动。这些波动以随机方式发生,并可能导致整个流体中形成涡流、涡旋和涡旋型态。
湍流的影响
湍流的影响
积极成果
●
增强传热:湍流改善对流传热,从而在热交换器和暖通空调系统等应用中实现更高效的冷却或加热。
●
能量耗散:湍流促进流体动能的耗散,有助于抑制振荡并减轻流体诱导力对结构的影响。
●
改善混合性和稳定性:湍流增强混合性,延迟流动分离,从而减少形状阻力,这在许多工业应用中都大有裨益。
负面后果
●
能量损失增加:流体流动系统中的湍流会导致更高的摩擦损失,从而降低整体效率。流体内剪切应力的增加会导致材料疲劳和设备磨损,进一步损害系统性能。
●
不可预测:湍流的复杂性使得预测流体行为变得极具挑战性,阻碍了工程系统的设计和优化。因此,工程师常常难以准确地建模和分析湍流系统。
●
不必要的混合:虽然湍流可以增强流体混合,但在需要不同流体层的应用(例如化学反应器)中,这可能是不利的。相反,湍流带来的混合和对流传热的增强会影响热交换器和热系统的效率,有时甚至会带来有益的影响。
●
不可控:与层流相比,湍流更难控制和稳定,这给各种流体动力学应用带来了重大挑战。湍流固有的不可预测性使得调节流速、温度和压力变得更加困难。
●
压力损失:与层流相比,湍流通常会导致更高的压降,从而增加流体输送系统的能耗。这会对系统设计和运行产生重大影响。
●
振动和疲劳:湍流会诱导浸没在流体中的结构产生振动,从而导致结构疲劳、潜在损坏以及工程系统中的能耗问题。因此,减轻湍流的影响对于确保这些系统的安全高效运行至关重要。
无序流动结构的特征
无序流动结构的特征
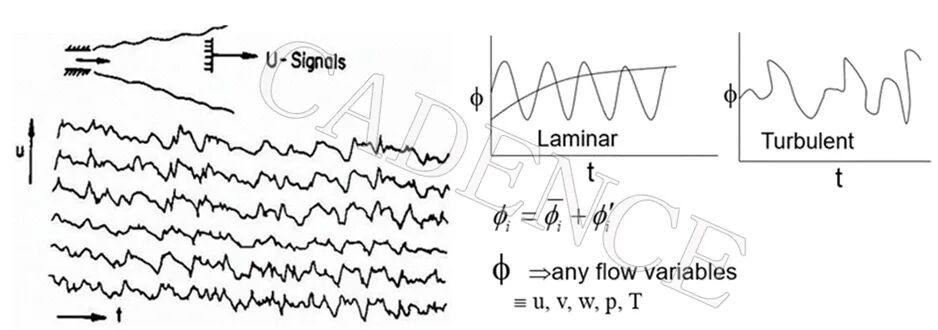
湍流系统表现出无序、混沌且看似随机的行为,因此很难预测其确切结果或型态。由于这些流动对初始条件高度敏感,即使是微小的变化也可能导致截然不同的结果。这意味着,即使是初始条件的微小变化也可能导致截然不同的结果,因此不可能重现完全相同的行为。湍流跨越了极其广泛的长度和时间尺度,从微小的涡流到巨大的大气运动。值得注意的是,即使是这些系统中最小的尺度也足够大,足以满足连续介质假设,该假设认为流体是连续的,而不是离散的。
湍流的一个标志是由于分子尺度的粘度而表现出增强的扩散(混合)和能量耗散特性。这意味着湍流系统在混合和分散物质以及将动能转化为热量方面非常有效。湍流本质上是三维的、随时间变化的和旋转的,这与层流不同。具体来说,旋转的存在是湍流的一个关键特征,因为它会导致涡旋和其他复杂结构的形成。另一方面,势流根据定义是无旋的,因此不可能是湍流。湍流的另一个决定性特征是其间歇性行为,其特点是空间和时间上都会出现一阵剧烈的活动,随后是一段相对平静的时期。这种不规则和不均匀的行为反映了复杂的动力学,使得湍流难以建模和预测。
长度和时间的尺度变化
长度和时间的尺度变化
湍流通常有四种主要尺度,分别描述流体运动的不同范围。这些尺度包括:
●
大尺度:此尺度由研究区域的几何形状决定,涵盖流动的整体尺寸和结构。
●
积分尺度或外尺度:此尺度约为大尺度的 10-20%。它用于衡量流动中蕴含能量的涡流。
●
泰勒微尺度:介于积分尺度和最小尺度之间,此中间尺度属于柯尔莫哥洛夫惯性子域。它表征了粘度效应开始影响流动的尺度,标志着从惯性范围到耗散范围的过渡。
●
柯尔莫哥洛夫尺度或内尺度:这是湍流尺度中最小的尺度,表示粘性力占主导地位且能量耗散的尺度。
值得注意的是,其他物理现象发挥重要作用的湍流中,可能涉及到额外的尺度,例如传热或燃烧。
参考文献:
“Turbulent Flows” by Pope Stephen B.
“Homogeneous Isotropic Turbulence” by J.L. Lumley.
Germano, M., Piomelli, U., Moin, P., and Cabot, W. H. (1991). A dynamic subgrid-scale eddy viscosity model. Physics of Fluids A: Fluid Dynamics (1989-1993), 3(7), 1760- 1765.
Hunt, J. C. R., Wray, A. A., and Moin, P. (1988). Eddies, Streams, and Convergence Zones in Turbulent Flows. Proceedings of Summer Program, Stanford University: Center for Turbulence Research, 193-208





