涡轮丨上交大:增材制造燃气轮机涡轮叶片的扰流柱三维形貌对流动换热影响机制研究
关键词:燃气轮机;涡轮叶片冷却;扰流柱;强化换热;增材制造;CT扫描
引言
引言
为了满足工程应用中对燃气轮机更高效率的追求,涡轮前入口温度在不断提高,目前已经远远超过金属所能承受的极限温度。为了避免涡轮叶片热烧蚀,冷却技术的引入是极其关键的。常用的冷却技术包括外部冷却和内部冷却,其中内部冷却通过把冷却空气通入叶片内部的专门通道进行冷却,其冷却性能依赖于内部通道的几何结构设计。扰流柱排列是增强内部冷却较为常见的结构布置。在实际应用过程中,叶片加工所引入的表面结构特征对扰流柱的换热性能影响往往是不能忽视的,因此厘清加工制造引入的表面特征在涡轮叶片内部扰流柱冷却过程中流动换热的影响一直是相关领域人员的关注方向。
作为典型的涡轮叶片内部换热单元,扰流柱冷却通过增大换热面积,增强流动掺混来增强内部表面的对流换热。国内外学者开展了大量关于扰流柱表面特征对其流动换热影响的相关研究。Pham等通过k-ω湍流模型仿真分析了C型端壁对于圆柱扰流柱换热方面的影响。Luo等提出了一种弯曲扰流柱的设计,并通过realizable k-ε数值模拟方法验证了其优于传统的右上扰流柱的换热性能。Zhou等采用SST k-ω模型研究了不同形状的扰流柱横截面(方形、圆形、椭圆形、NACA叶型轮廓和水滴形)对扰流柱换热的影响,发现椭圆形和NACA叶型轮廓的扰流柱换热最好。Yeranee等同样研究了不同形状的扰流柱(圆柱、方菱形、三角形和优化型)的流动换热性能,数值模拟发现优化型结果从增强流动掺混和增加换热面积两个方面起到了对换热的增强作用。除了几何形状,一部分学者研究了扰流柱表面粗糙度对流动换热的影响。Buresti通过开放式喷气风洞实验,研究表面粗糙度对圆柱绕流中亚临界、临界、超临界和过临界状态转变的影响。雷诺数在2.6×104~2.8×105,相对粗糙度在1.0×10−3~12×10−3,实验证实了粗糙度对扰流流态的显著影响,特别是粗糙度可以缩短过渡区域,在高粗糙度的圆柱中甚至可能消失。李广超等模拟并分析了在不同粗糙度下,雷诺数在Re=1×104~5×104的局部和平均努塞尔数分布,发现粗糙度的增加使扰流柱表面平均换热系数增大;雷诺数越大时,粗糙度对换热系数的影响越明显。根据以上的研究可以发现,扰流柱及其端壁的表面形貌特征对于其本身的流动换热特性影响是显著的。
目前,随着金属增材制造技术的成熟发展,新的加工方式引入的特殊表面结构对加工件应用过程中流热方面的影响亟需开展相关的评估研究。Kaur等通过X射线计算机断层扫描(CT)扫描和光学轮廓仪对增材制造部件进行了表面形貌获取,并以此进行数值模拟建模,研究了其对十四面体晶格的流动换热的影响。增材制造方法在涡轮叶片冷却领域同样开始普及,Snyder等采用CT扫描技术获得了不同加工角度的气膜孔样,扫描的结果表面气膜孔内部流道的加工偏差受到加工角度明显的影响。Furgeson等同样采用CT扫描技术获得了某种增材制造型孔的内部流道特征,发现气膜孔的实际直径要大于设计值,而气膜孔壁面厚度则略小于设计值。可以发现,增材制造对叶片气膜冷却孔的影响是比较显著的,但是目前有关涡轮叶片扰流柱的增材制造表面形貌表征以及相关的流动换热影响研究较少。
因此,本文研究的出发点正是基于CT扫描技术分布,获取增材叶片和传统铸造叶片内部扰流柱几何结构与表面特征,通过直接对加工的扰流柱进行计算域的建模,采用数值模拟的方式探讨两种加工方式的表面结构对扰流柱单元流动换热的影响。研究结果首先将与典型圆柱绕流努塞尔数实验关联式进行验证,后续从努塞尔数、流动损失等方面进行讨论分析。
方法
方法
2.1 叶片加工与扰流柱形貌提取
本文首先通过金属铸造和增材制造分别获得了两种加工方式下的某实验型号涡轮叶片。为了获取叶片内部冷却通道内的扰流柱及其两端壁面的表面特征,常规的光学形貌测量方法是无法实现的。参考Kaur等通过X射线计算机断层扫描(CT)法对燃气轮机叶片尾缘针翅结构表面形貌扫描的方法,本文采用相同的方法对本实验获得的真实叶片进行扫描,具体测量方法如图1(a)所示,通过把测试叶片的尾缘部分放置在旋转载物台上环形扫描即可获得其内部的形貌特征。对叶片扫描后,实际加工获得的叶片模型如图1(b)和(c)所示。
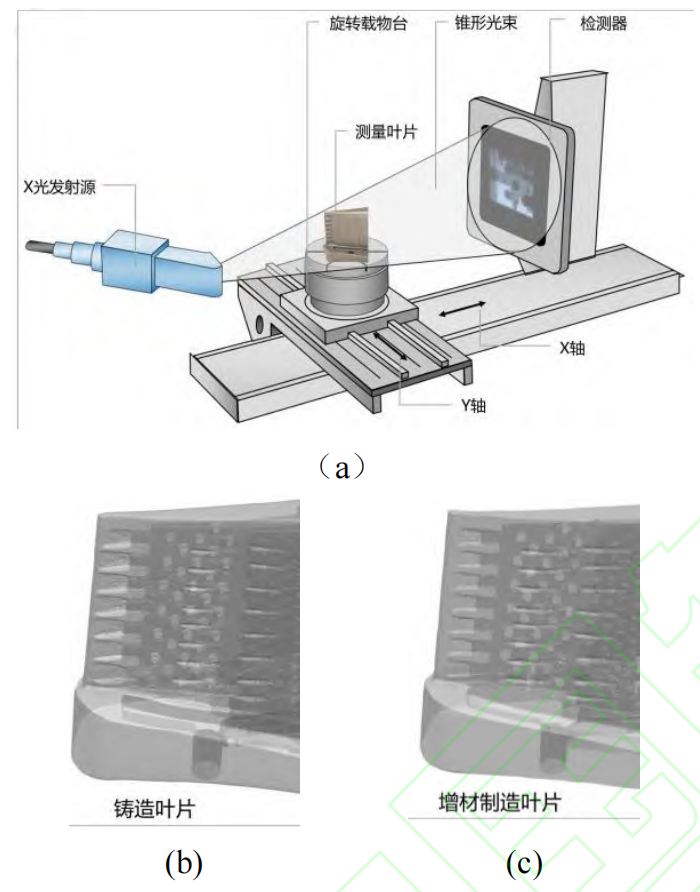
图1 计算机断层扫描(CT)法获得的叶片模型
本文的研究目标是某实验型号涡轮叶片内部的扰流柱单元,采用CT扫描的方法分别扫描了叶片内多个扰流柱的表面形貌,获取了两种加工制造方式下的扰流柱单元模型各个位置的平均表面粗糙度。随后测量了同一排6个扰流柱的直径,选取了其中具有代表性的扰流柱单元开展后续的研究,该扰流柱的表面形貌特征与未选择的扰流柱是相似的,且直径最接近6个扰流柱的平均直径,如图2所示。具体的扰流柱形貌如图3所示,选取了从扰流柱根部的向上的7个截面的数据进行两种加工方式下典型扰流柱形貌的分析,其中各处的截面的水利直径dₙ与圆形度φ的计算公式如下:
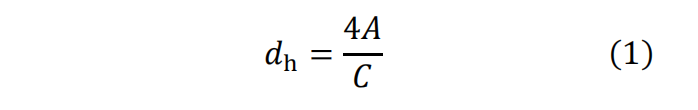
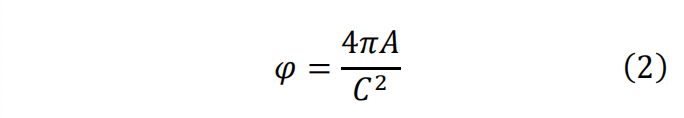
式中A为各个截面的面积,C为各个截面的周长,光滑扰流柱在叶片内的设计直径为1mm。通常,圆形度φ的取值在0~1之间,等于1则表明是标准的圆,越接近1表示该截面接近圆形,远小于1时表示该截面形状偏离圆形,可能是不规则或者是椭圆等。
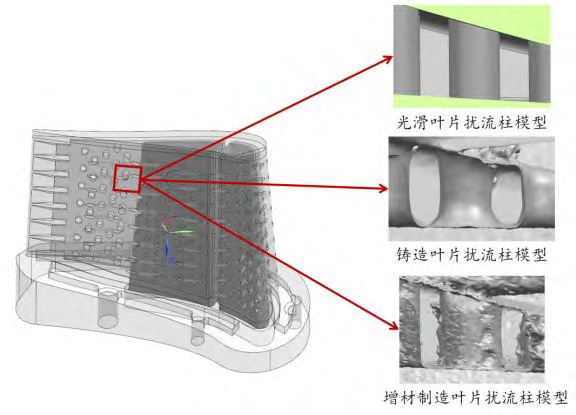
图2 扰流柱单元提取
图3表明铸造扰流柱的直径变化较大,扰流柱与端壁连接处呈现扩张的喇叭状,但是圆形度比较接近1;增材制造扰流柱的直径变化较小,但是存在很多不规则的截面,这是因为在金属粉末固化过程中温度控制不均匀,扰流柱表面存在更多的加工缺陷,也表现得更加粗糙。
表1总结了7个截面上扰流柱直径与圆形度的统计数据,其结果与图3观察到的结果是一致的,并且增材制造的扰流柱平均直径要大于铸造扰流柱。此外,根据CT扫描获得的上下端壁及扰流柱形貌,计算了三个表面上的算术平均粗糙度Ra,具体结果如表2所示。可以发现铸造所引入的表面粗糙度要小于金属增材制造所引入的表面粗糙度,其中金属增材制造的上壁面粗糙度要远大于铸造所引入的粗糙度。相较于铸造,增材制造引入的粗糙度在三个面上平均增加了85%的粗糙度。后续的研究正是基于实际加工获得的扰流柱形貌进行计算域的简化建模,同时将光滑扰流柱作为对比基准。
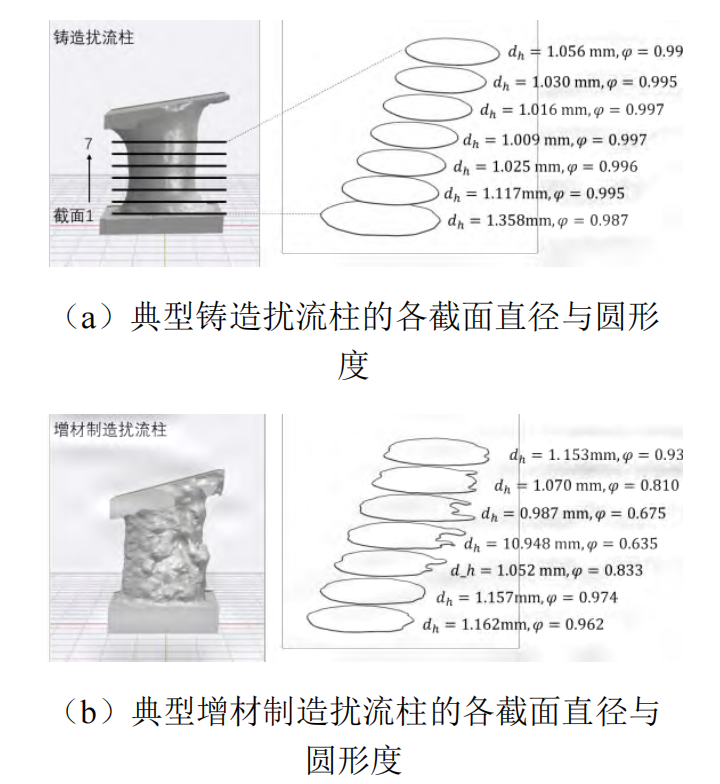
图3 两种加工方式扰流柱形貌对比
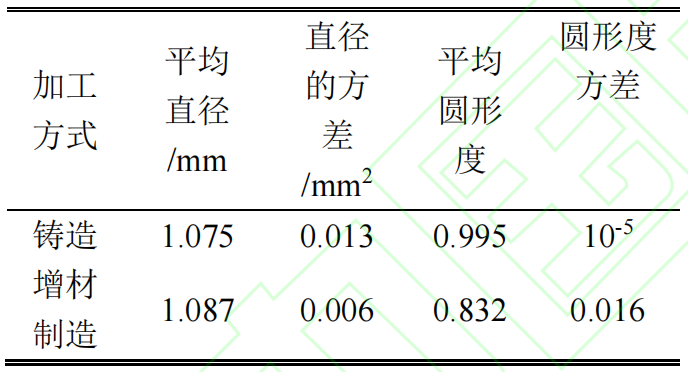
表1 不同加工方式下扰流柱形貌统计量
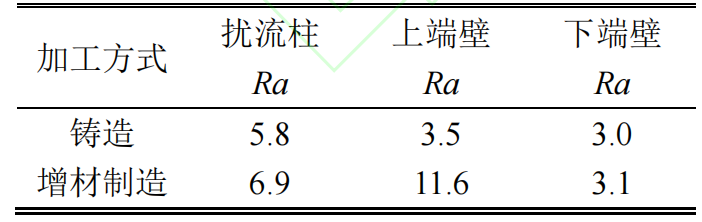
表2 不同加工方式下的扰流柱及上下端壁算术平均粗糙度Ra(单位:μm)
2.2 数值模拟验证
为了匹配雷诺数以及后续圆柱绕流实验关联式的验证,本文将光滑扰流柱放大8倍(D=8mm)进行计算。由于对于单个扰流柱单元的附近端壁曲率变化不大,计算域模型的上下端壁简化为平直壁面,夹角与扰流柱所处位置的上下壁面夹角一致,经过测量为12.6°。整个计算域几何参数如图4所示,除了光滑壁面的扰流柱外,还建立了铸造和金属增材制造获得的扰流柱计算域模型,铸造和增材制造扰流柱根据表1中的平均直径放大到8mm。
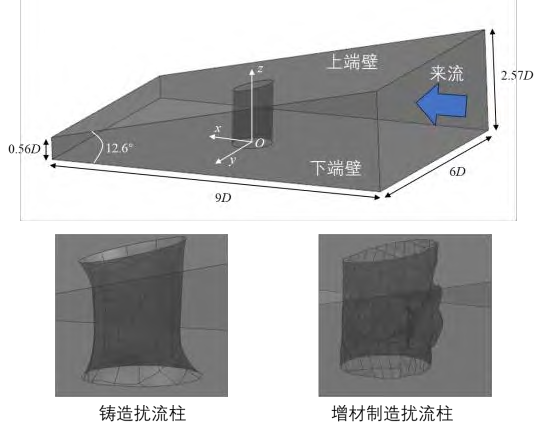
图4 扰流柱单元计算域
根据以前学者对扰流柱研究采用的湍流模型,本文采用SSTk-ω湍流模型来计算扰流柱附近的流动与换热。在进行本文的数值模拟研究之前,首先需要对湍流模型进行验证。模型验证的计算域如下图5所示,速度入口按照不同的雷诺数(Re=2917、5835、9725、14587)分别设置,雷诺数定义见式(3),来流温度为318.15K;出口静压为0.1MPa,温度为318.15K;上下壁面与圆柱壁面设置为恒温壁面,温度为298.15K;前后两边则为周期性边界条件。圆柱中截面的热流密度通过数值模拟获得,温差已知,因此数值模拟的圆柱中间截面上的平均努塞尔数可由式(4)获得。


从表3可以看出,随着雷诺数的增大,努塞尔数的增强表面圆柱表面的换热是增强的。同时雷诺数越大,仿真获得的圆柱绕流平均努塞尔数与实验关联式所计算的相对误差越小。当雷诺数大于9000左右时,预测误差在3%以内。同时本文对比了在高雷诺数条件下圆柱表面随角度θ变化的局部努塞尔数分布,从图6可知,仿真结果与实验结果的量值与趋势是一致的,预测的回升点均在80°左右,因此湍流模型的选择是合理的。
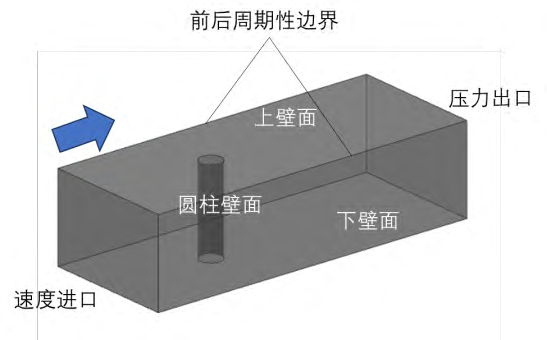
图5 湍流模型验证计算域模型
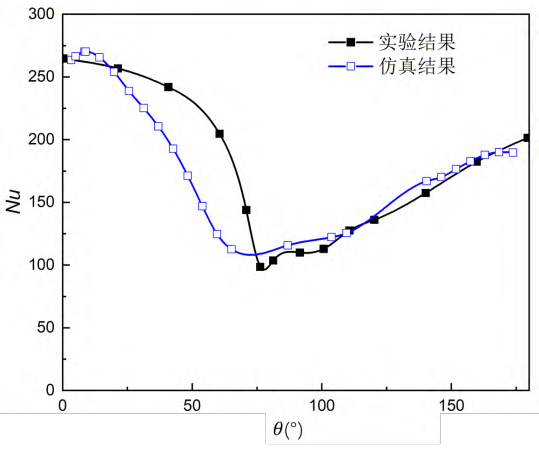
图6 局部努塞尔数分布(Re=70800)
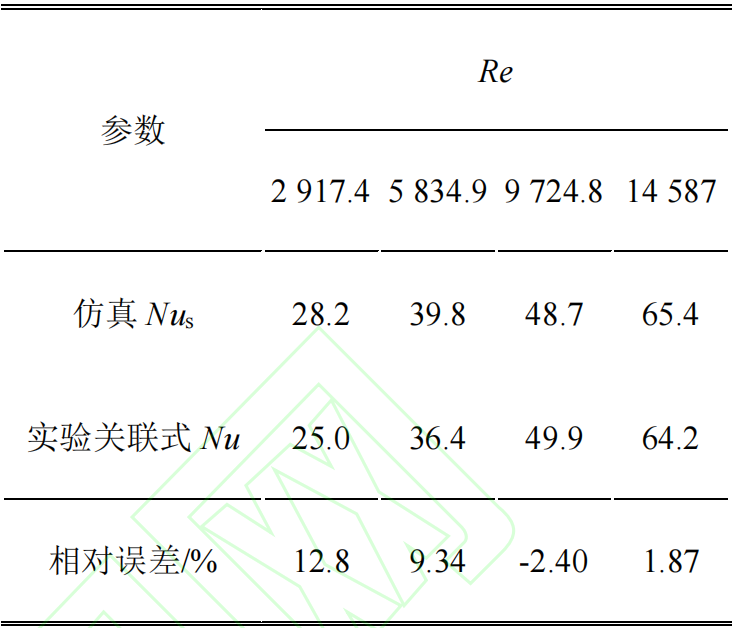
表3 不同雷诺数卜仿真与实验关联式获得的圆柱周向
平均努塞尔数对比
对于带有增材制造特征的扰流柱单元计算域,采用Fluent meshing进行多面体网格的划分,网格的细节如图7(a)所示,在扰流柱的壁面上对网格进行了加密,同时在所有壁面上附加了棱柱层网格,第一层网格厚度为了保证复杂形状扰流柱表面的计算精度,保证y+在1左右。为了验证网格无关性,本文计算了平均努塞尔数随网格数目的变化和扰流柱前缘驻点位置沿着z方向上压力随网格数目的变化曲线,分别如图 7(b)和(c)所示。从结果可以看出,随着网格数目的增加,换热和压强结果随着网格数目改变而变化的幅度在逐渐减小,当网格数目大于15万时,计算结果可以认为已经趋于稳定,考虑到计算效率与计算准确度,后续的光滑扰流柱、铸造扰流柱和金属增材制造扰流柱均按照15.5万网格的生成方式进行构建。
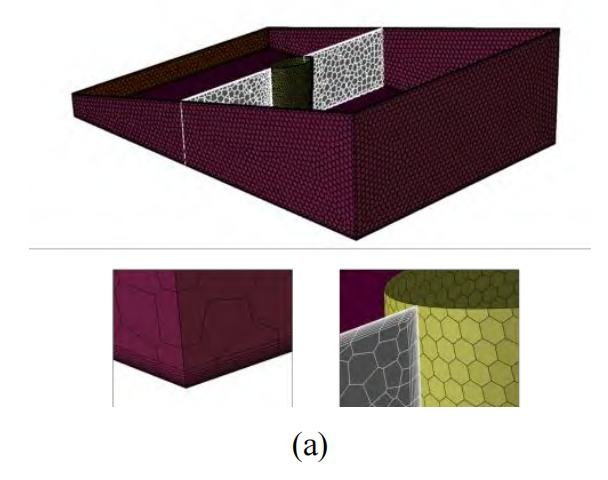
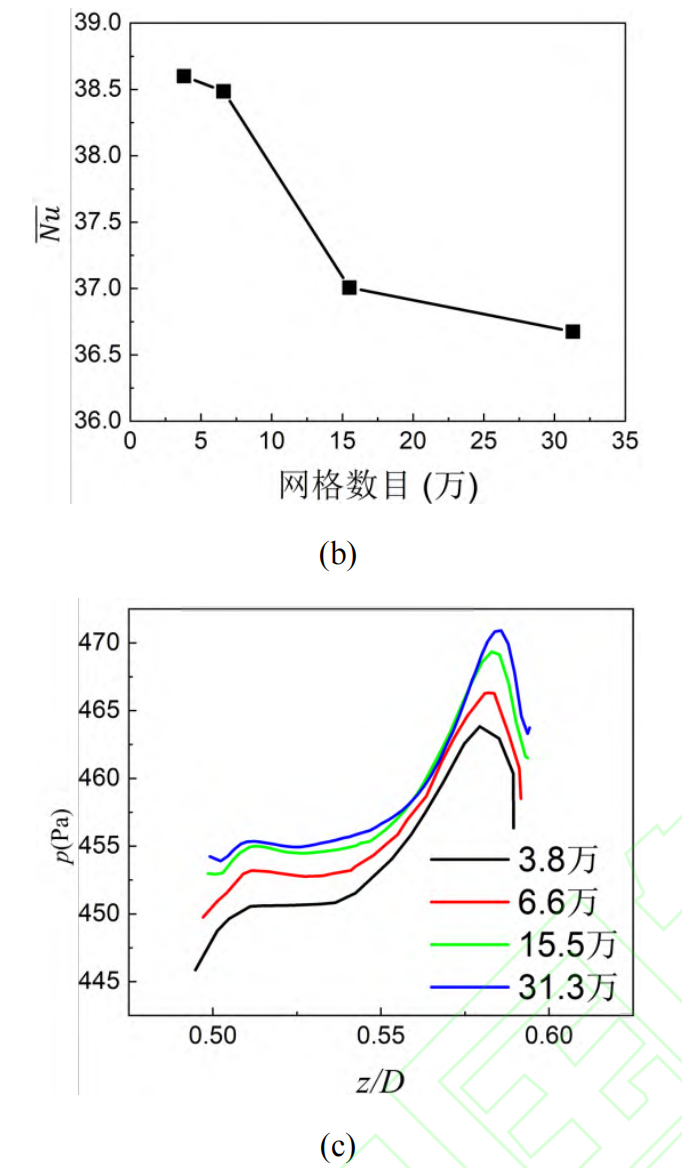
图7 计算域多面体网格划分与网格独立性验证
结果与讨论
结果与讨论
在验证完湍流模型的合理性和网格数目的无关性后,将与验证湍流模型时采用的边界条件设置赋予后续的扰流柱单元计算域。其中扰流柱本身保留CT扫描获得的表面形貌特征。上下端壁则根据FLUENT内部常用的沙砾模型赋予粗糙度,其中等效沙砾直径Ks按照式(6)的变换关系分别计算并设置,粗糙度均匀度Cs默认为0.5。为了验证此类壁面粗糙度添加方法的可靠性,根据粗糙壁面圆柱绕流的换热实验结果,首先在图5的计算域中的圆柱表面赋予了Ks/D=900×10−5量级的粗糙度,随后进行了两个不同来流雷诺数下的验证,将仿真获得的平均努塞尔数与实验经验关联式结果进行对比,其中光滑壁面采用式(5)进行计算,粗糙壁面采用式(7)进行计算,表4中结果显示仿真计算的换热努塞尔数与实验结果的相对误差均在5%以内,并且在壁面添加均匀粗糙度能够增强壁面的换热。
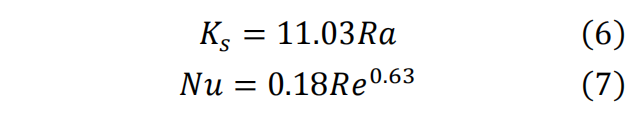
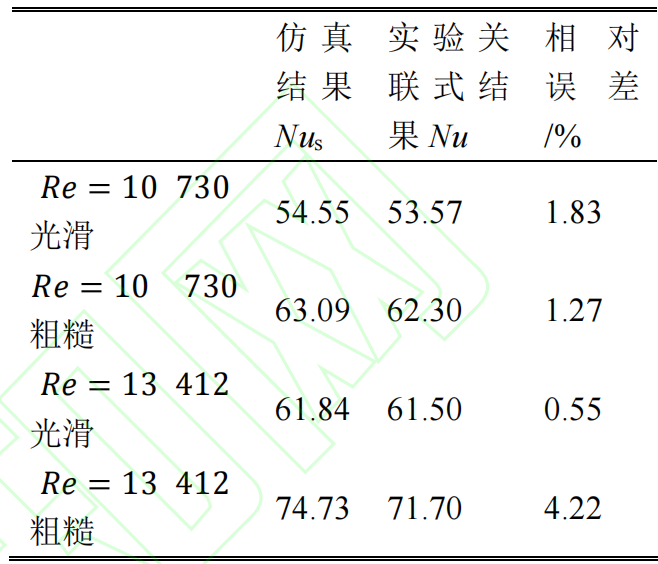
表4 圆柱周向平均努塞尔数对比验证
后续正式计算的工况除了加工方式不同的扰流柱计算域以外,本文还研究了不同来流雷诺数(Re=8536、17071、25606)下对扰流柱流动换热的影响,雷诺数范围涵盖了叶片内部扰流柱内的大多数来流情况,本节后续将讨论数值模拟结果。
3.1 不同加工方式下的扰流柱流场分析
为了进一步分析增材制造加工的扰流柱对内部流动的影响,本文提取了z/D=0.5平面上的流场进行分析。图8显示了Re=17071时z/D=0.5平面上的流线以及标准化速度云图,其中光滑扰流柱和铸造扰流柱在该平面上的流场是比较对称的,而金属增材制造获得的扰流柱因其表面突起的不对称性,从扰流柱右侧经过的流体出现分离壁面的现象要早于光滑扰流柱,流体分离后的扰流柱壁面努塞尔数将因此大幅减小。
图9绘制了Re=17071下的z/D=0.5平面上的湍动能云图,其中湍动能使用入口速度的平方进行了归一化处理。可以看到金属增材制造扰流柱下游的湍动能水平最高,光滑扰流柱的最低。湍动能越大,说明该区域的湍流水平越高,能量掺混传递的越快,越有利于该区域对应端壁的换热。此外,由于增材制造引起的扰流柱不对称性在湍动能分布上的表现更加明显,铸造和金属增材制造扰流柱均表现出了较为明显的湍动能不对称分布。
最后,图9对比了不同雷诺数下各种加工方式的扰流柱的阻力因子大小。阻力因子的定义如下式:
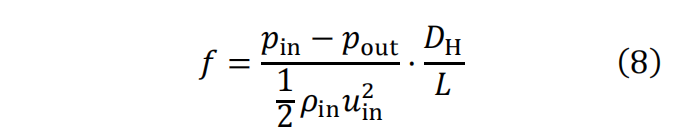
式中𝑝in和𝑝out分别为流体域入口和出口的压力,𝜌in为入口处来流的密度,𝐷H为入口水力直径,𝐿为整个计算域长度。对于所有工况,随着雷诺数的增大,阻力因子不断增大,其中铸造的扰流柱在低雷诺数下阻力因子要略小于光滑扰流柱,这主要是由于铸造扰流柱表面在靠近中部区域的直径较小,使得其对流道的阻塞面积小导致的;铸造扰流柱与端壁之间为渐扩连接,衔接更加光顺,能够减小马蹄涡等二次流的流动损失。而在高雷诺数下,由于壁面粗糙度导致摩擦引起的损失占主导,因而铸造扰流柱的阻力因子大于光滑扰流柱的。对于金属增材制造加工获得的扰流柱,由于其表面粗糙度远大于另外两种构型,其阻力因子在不同工况下都是最大的,并且在高雷诺数下损失系数要明显高于光滑和铸造扰流柱扰流柱。其中,在本文雷诺数研究范围内流经金属增材制造获得的扰流柱时阻力因子最大,最大流动损失增加了1.6%。
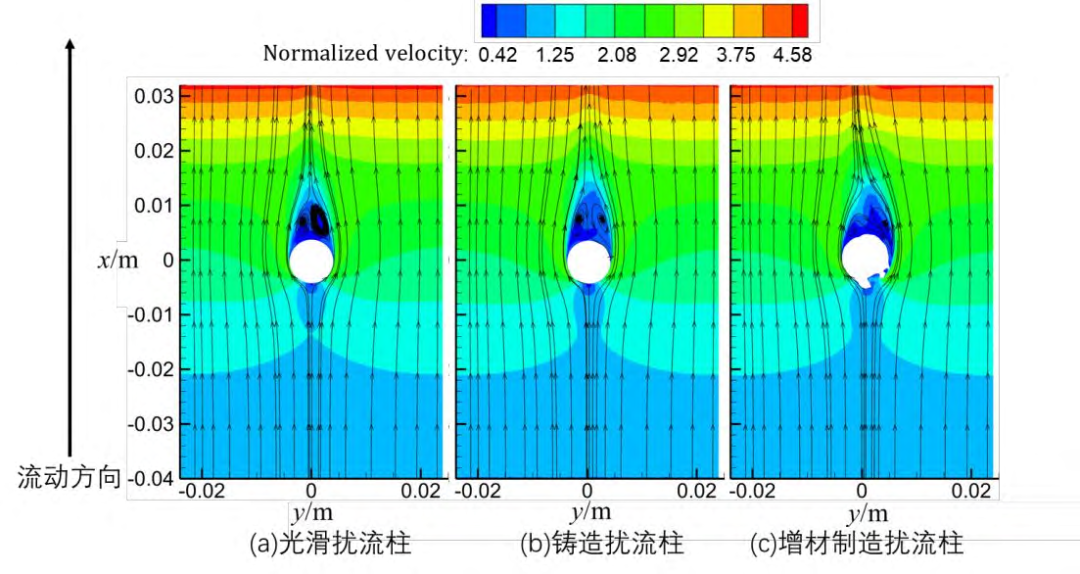
图8 三种扰流柱的绕流流场(Re=17071,z/D=0.5)
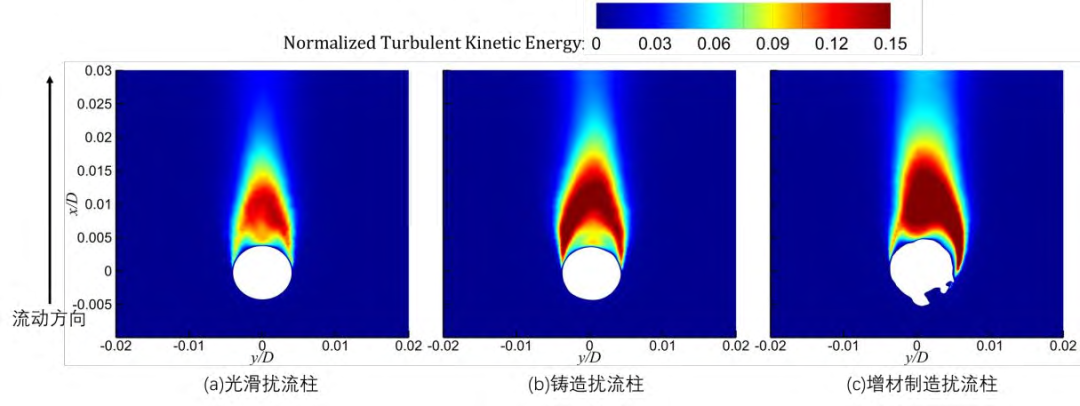
图9 三种扰流柱下游的湍动能分布(Re=17071,z/D=0.5)
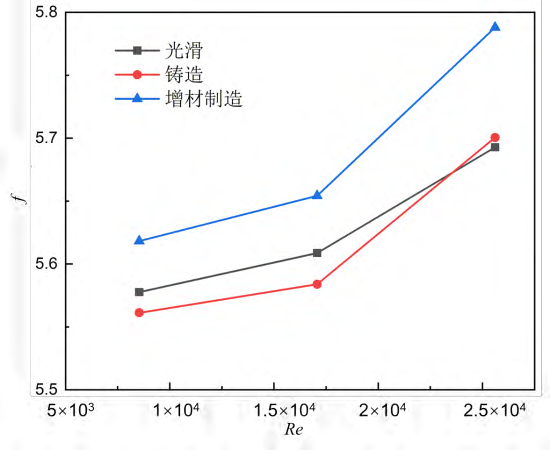
图10 扰流柱单元的阻力因子𝑓随雷诺数的变化
3.2 不同加工方式和雷诺数对扰流柱表面努塞尔数的影响

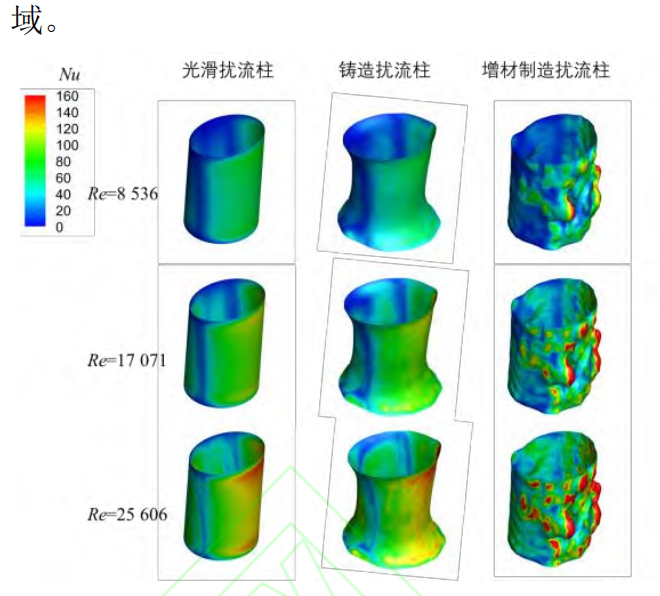
图11 不同加工方式和雷诺数下的扰流柱表面努塞尔数分布
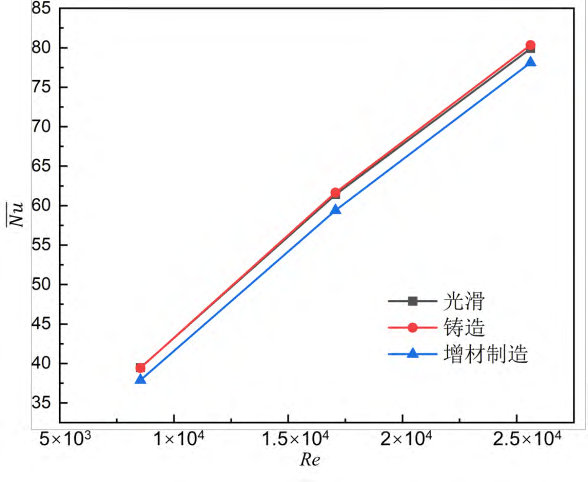
图12 扰流柱的面平均努塞尔数随雷诺数的变化
3.3 不同加工方式和雷诺数对上下端壁表面努塞尔数的影响

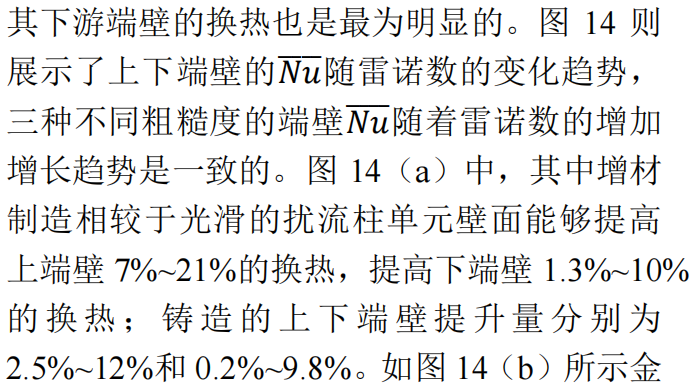
属增材制造粗糙度下的下端壁换热仅仅略强于铸造粗糙度的,并且二者也是要大于光滑下端壁的换热。粗糙度对换热的增强随着雷诺数的增加也愈发明显。需要注意的是,不同于上节中扰流柱表面的换热结果,由于端壁并未引入真正的形貌而是仅仅设置了粗糙度数值变化,所以相较于光滑端壁,铸造和金属增材制造的上下端壁的换热均得到了增强。

图13 不同加工方式和雷诺数下的上下端壁表面努塞尔数分布
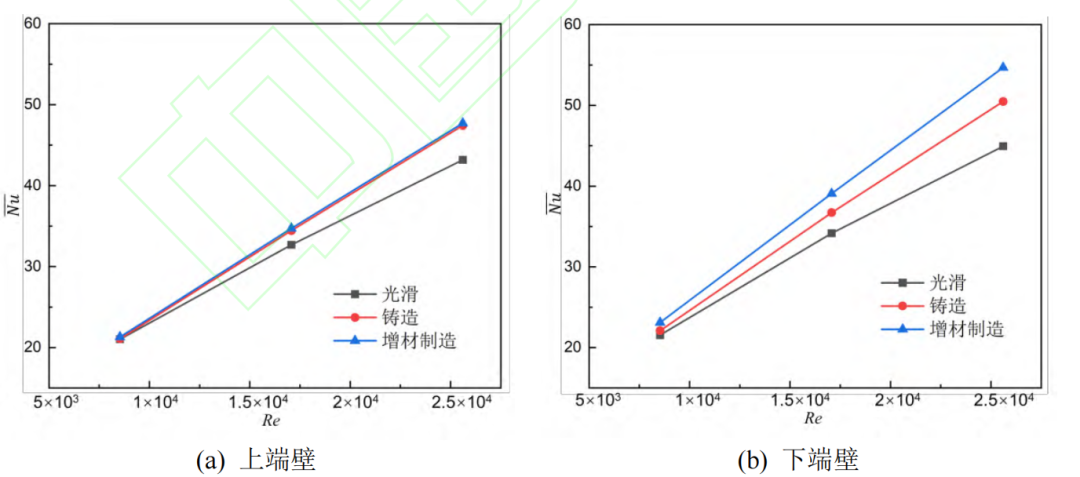
图14 上下端壁的面平均努塞尔数随雷诺数的变化
结论
结论
本文通过研究,得到如下结论:
(1)相较于铸造工艺,增材制造加工方式引入的粗糙度在三个面上平均增加了85%的粗糙度,其扰流柱的平均圆形度为0.832,铸造的为0.995,同时增材制造扰流柱沿径向的直径变化要大于铸造扰流柱;
(2)扰流柱能够增强下游的湍动能,从而增强掺混,提高扰流柱端壁的换热,并且端壁的粗糙度越大,换热越强。其中增材制造方式相较于光滑的扰流柱单元壁面能够提高上端壁7%~21%的换热,提高下端壁1.3%~10%的换热;铸造的上下端壁提升量分别为2.5%~12%和0.2%~9.8%。
(3)除了能够增强换热,增材制造引入的表面形貌以及端壁粗糙度会增大流动损失,其中金属增材制造的扰流柱最大增加1.6%的流动损失。
(4)本研究范围内,考虑加工引入的表面特征,相较于光滑扰流柱,铸造工艺下引入的表面形貌能够略微提高扰流柱表面的努塞尔数;而增材制造工艺下引入的表面形貌会导致扰流柱表面流动死区较多,绕流流动过早分离,进一步地将轻微削弱扰流柱本身的换热。





