基于Abaqus的大变形自适应网格划分技术实例
Abaqus的ALE(Arbitrary Lagrangian-Eulerian,任意拉格朗日-欧拉)自适应网格划分是一种用于处理大变形问题的技术,允许网格独立于材料移动,即使在发生大变形或材料丢失时,也可以在整个分析过程中保持高质量的网格。ALE是在Abaqus默认的Lagrangian算法(网格随材料同步变形,适用于小变形)基础上,增加网格自适应划分技术,因此可以把ALE看做是默认Lagrangian的增强版,在保留Lagrangian优势的同时,又引进了自适应网格划分技术,减少了大变形时的网格畸变。由于ALE自适应网格划分不改变网格的拓扑结构(不创建或删除单元),这意味着该方法在极端变形情况下保持高质量网格的能力有一定的局限性,比如流体流动极端的变形分析,此时使用ALE可能仍然得不到可靠解,那就要用到纯Eulerian法了。ALE又可分为Abaqus/Explicit ALE和Abaqus/Standard ALE,Abaqus/Explicit ALE主要用于模拟大变形问题,Abaqus/StandardALE主要用于声学领域,并用于模拟材料烧蚀或磨损。本文只针对Abaqus/Explicit ALE展开论述。
Abaqus/Explicit ALE自适应网格可作为连续自适应网格划分工具,用于大变形的瞬态分析问题(如动态冲击、穿透和锻造问题),在预计会有大变形的问题中,自适应网格划分所带来的网格质量的提高可以防止由于严重的网格畸变而导致分析终止。在这些情况下,可以使用自适应网格来获得比纯Lagrangian分析更快、更准确、更健壮的解决方案。本文中,主要讨论以下问题:正弦形状的模具向下运动,使矩形截面的橡胶坯件变形,分析橡胶坯件的受力情况,见图1。
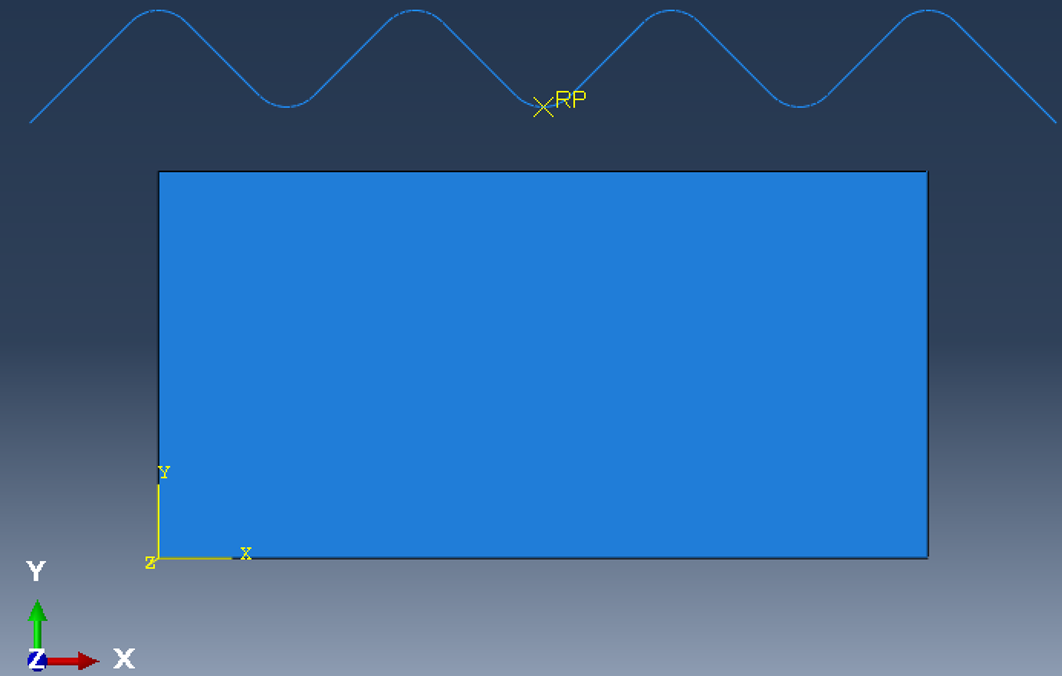
图1 模具挤压橡胶坯件
具体步骤如下:
1. 模型的建立
橡胶坯件、模具分别使用二维可变形、解析刚体来表征,见图2。
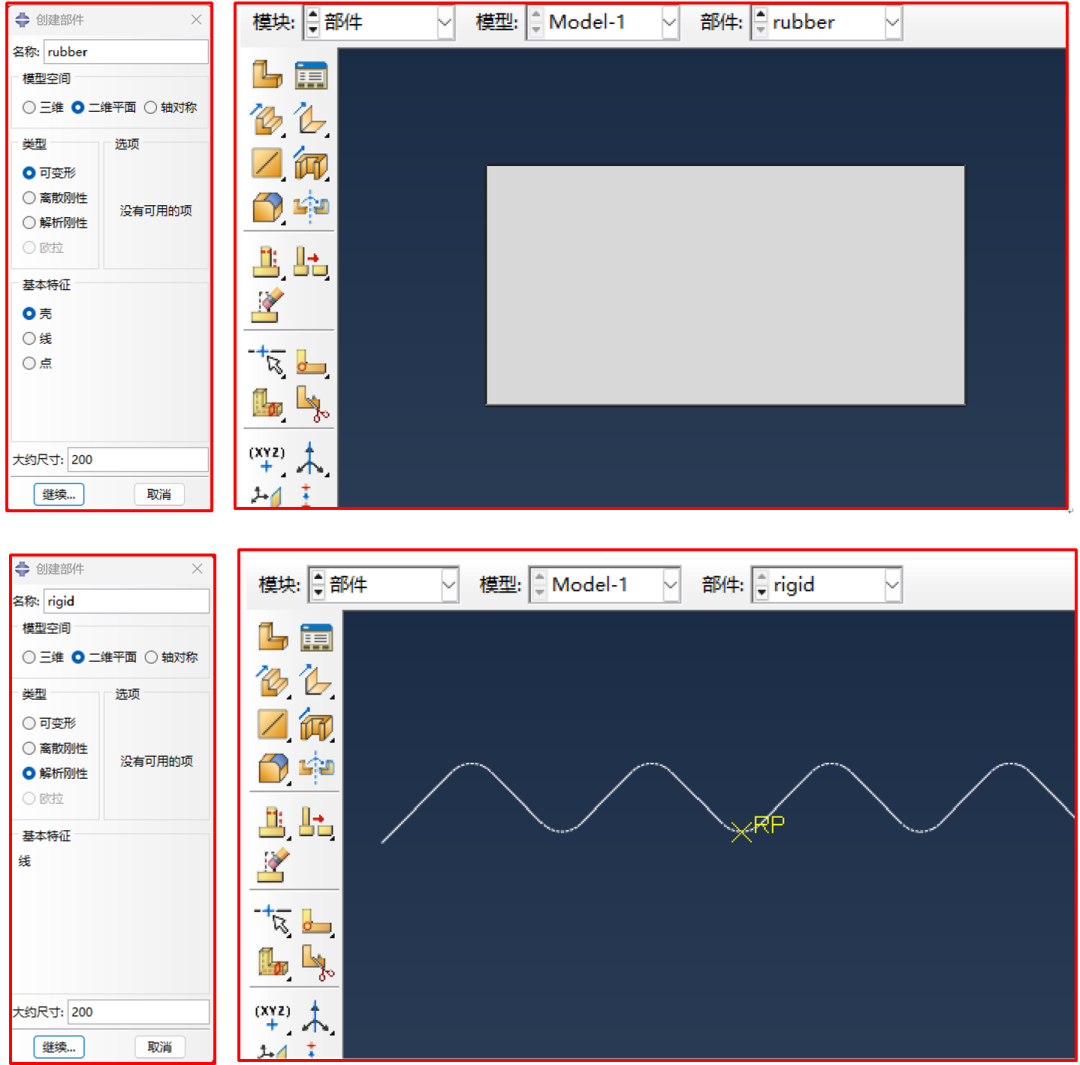
2. 材料属性的设置
设置橡胶材料属性,赋给坯件,模具使用解析刚体来表示,因此不需要赋予材料。
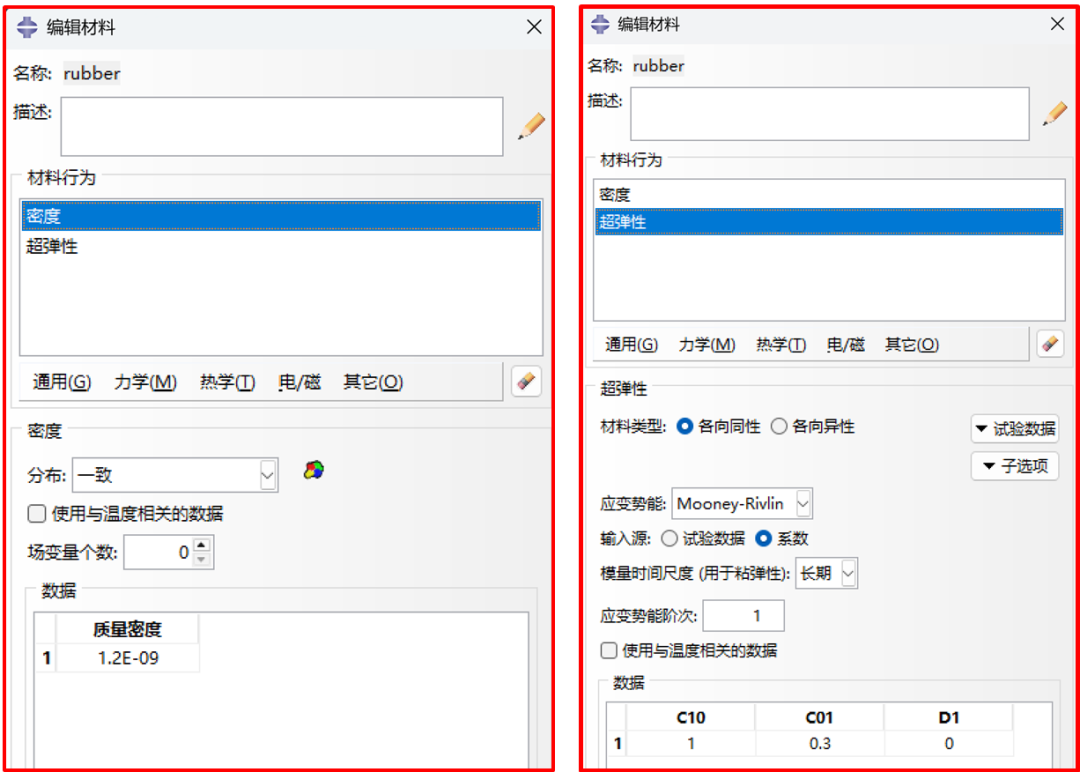
图3 橡胶属性设置
3. 装配体的生成
把以上两个部件按图1位置装配。
4. 分析步的设置
分析类型选择“动力,显式”,时长为0.1s,打开几何非线性,增量步采用默认设置。
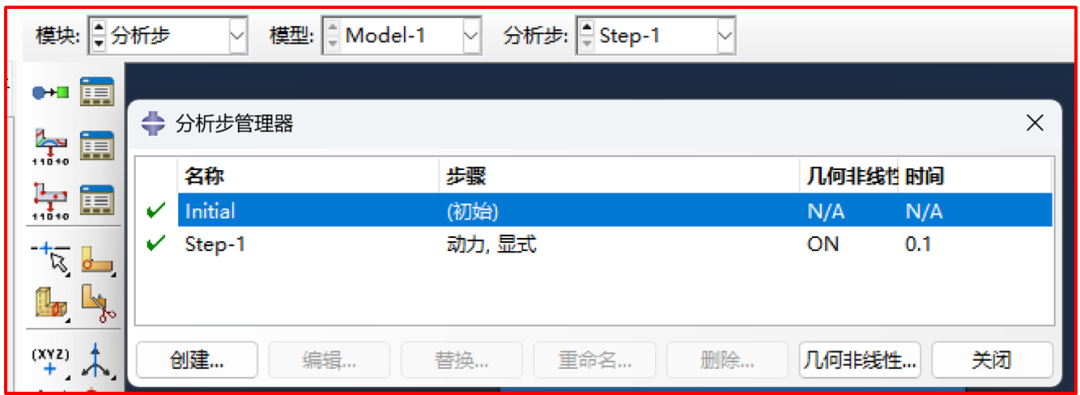
图4 设置分析步
设置好了分析步,就开始设置ALE自适应网格划分,在分析步模块中,选择“其他>ALE自适应网格区域>管理器”,见图5。
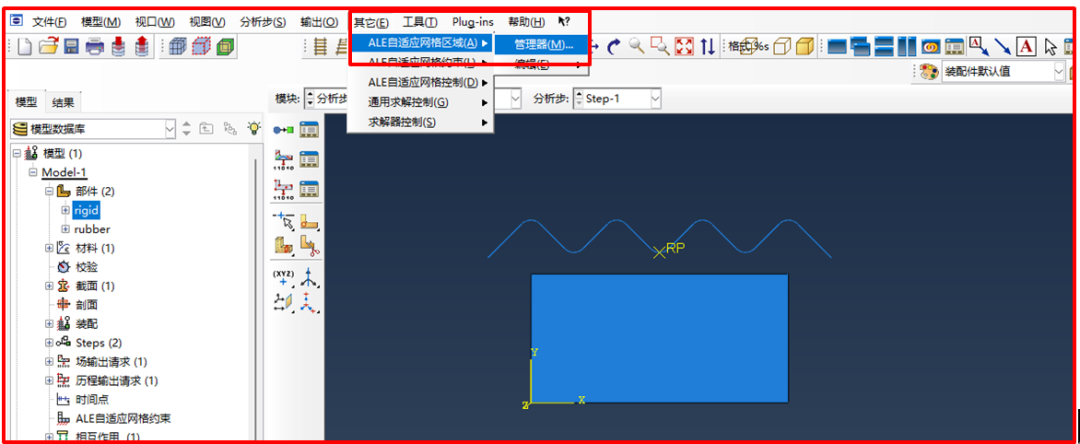
图5 创建ALE
弹出设置ALE设置界面,区域选择整个橡胶坯件。“频率”是指多少个增量步重新划分网格,这个值应该取小一些,“对每个增量步重划扫掠网格”是指每增量重新划分网格的次数,这个值可以取大一些。自适应网格控制可以采用默认设置,见图6。
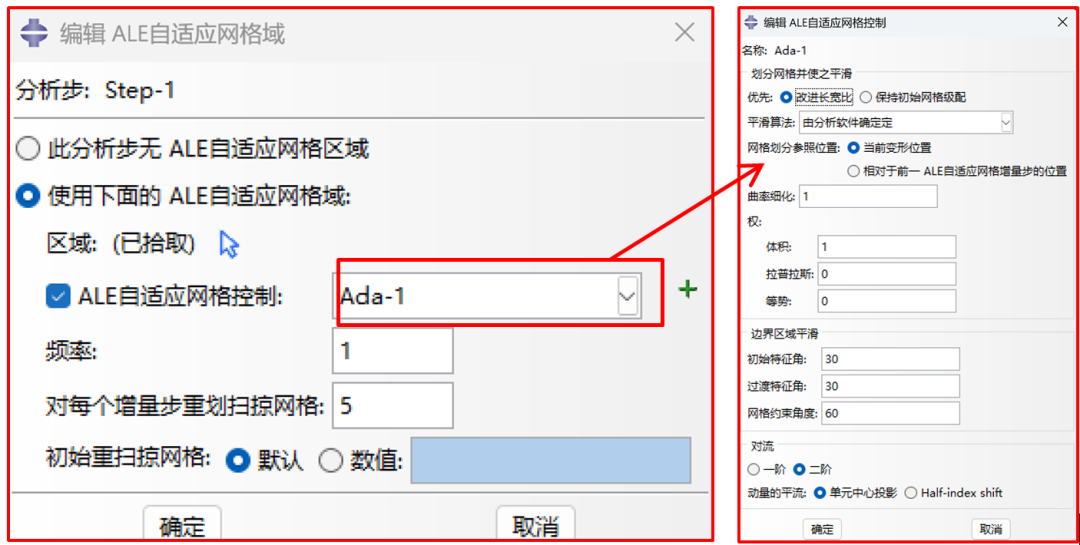
图6 编辑ALE
5. 相互作用的设置
在此处只需要设置模具挤压橡胶坯件时的接触,采用“面-面”接触,第一、二表面分别选择模具下表面、橡胶坯件上表面,见图7。
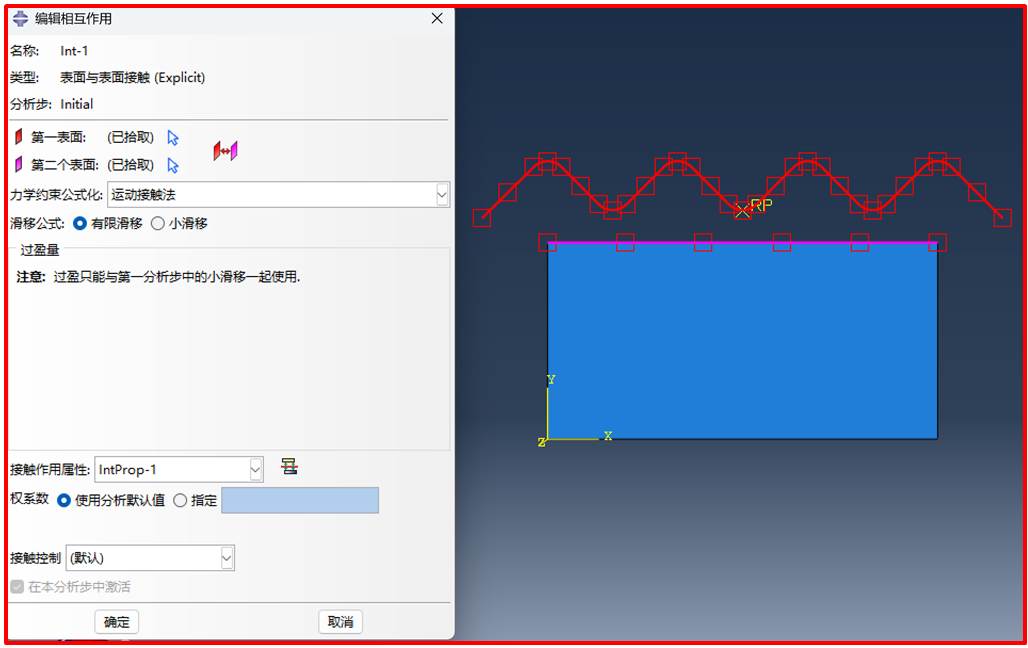
图7 “面-面”接触设置
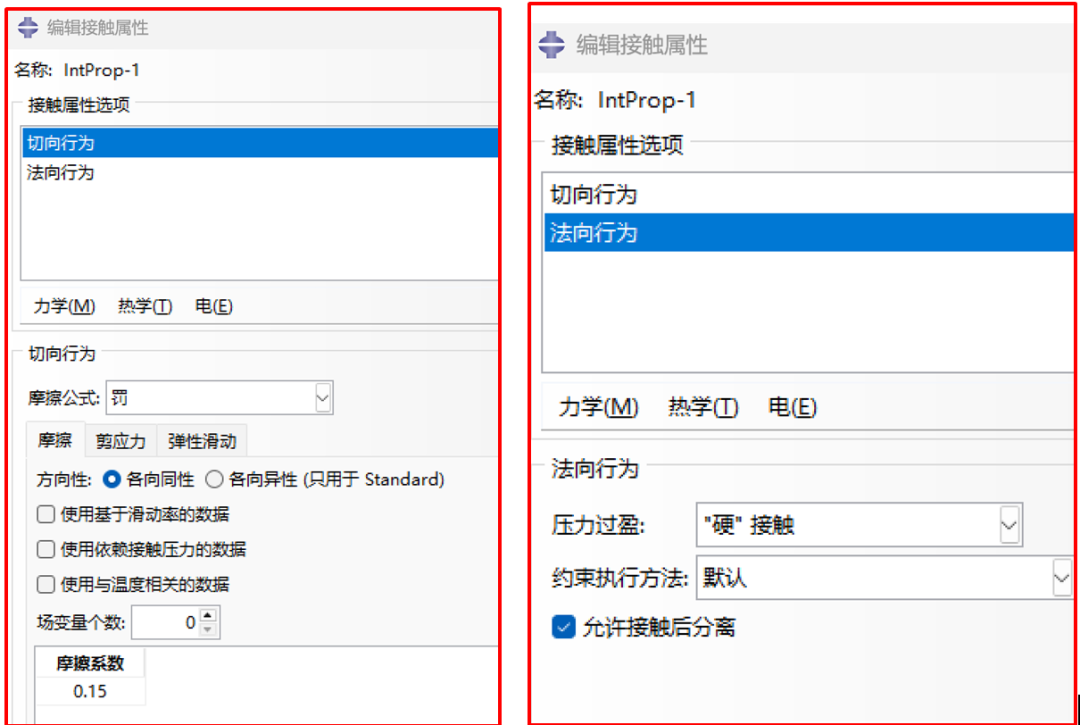
图8 接触属性
6. 约束与载荷的施加
为了方便施加约束与载荷,建立两个集,见图9。
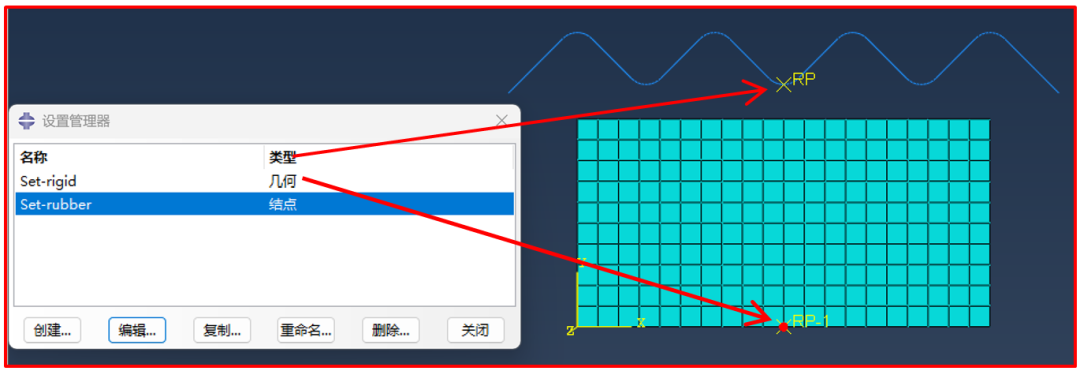
图9 创建集 合
橡胶底面设置Y方向约束,底面的中点设置X方向约束,这样设置是为了橡胶件在X方向能自由压缩。刚体的中点(即RP处)施加Y方向-20mm的位移,详细设置见图10。
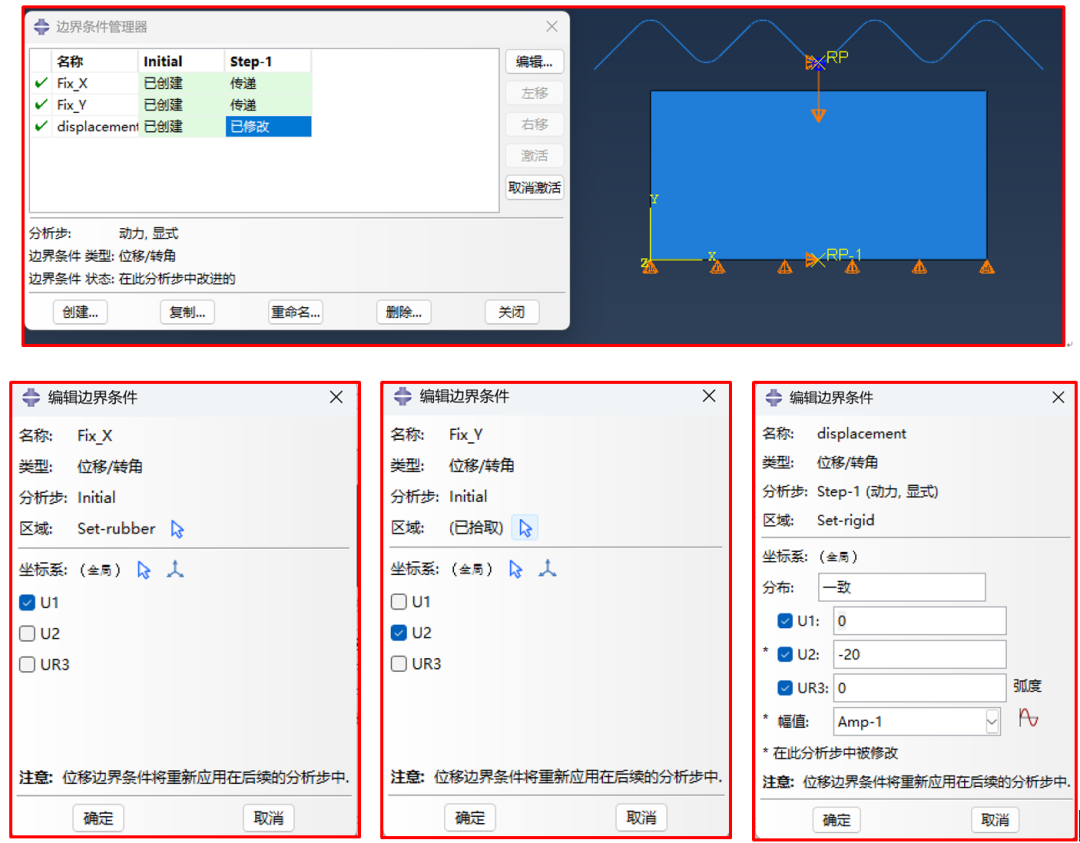
图10 约束、载荷的施加
7. 网格划分
对橡胶坯件进行网格划分,在设置单元类型时,需要特别注意:使用ALE自适应网格划分,几何阶次只能选择低阶线性,需要选择基于刚度的沙漏控制。见图11。
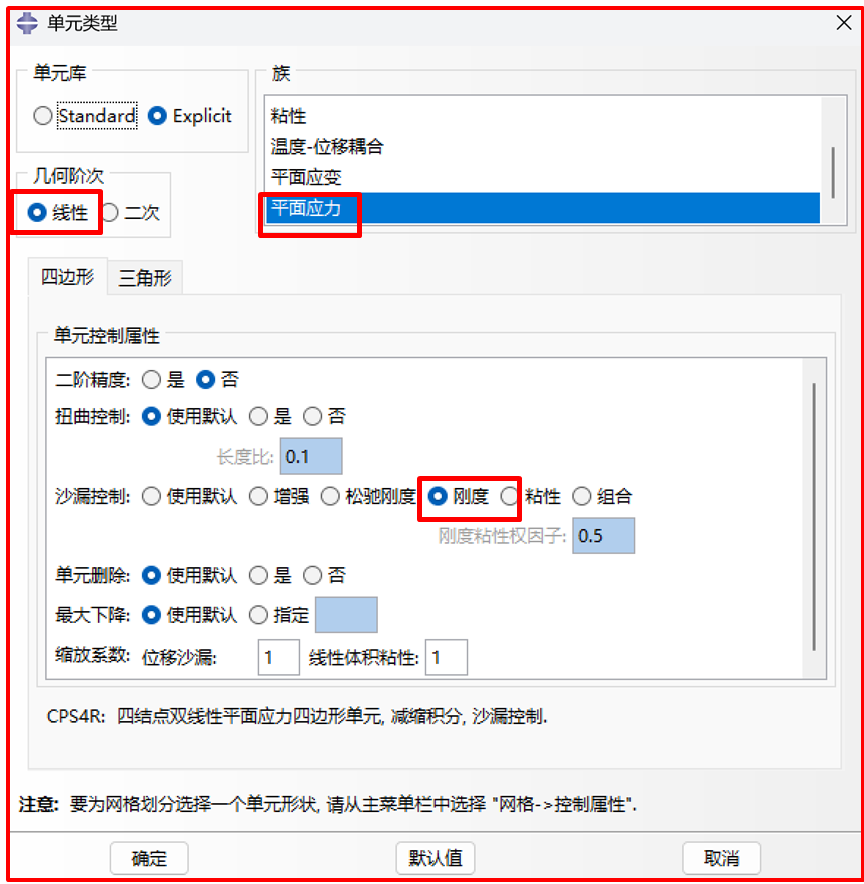
图11 单元类型的设置
8. 提交计算
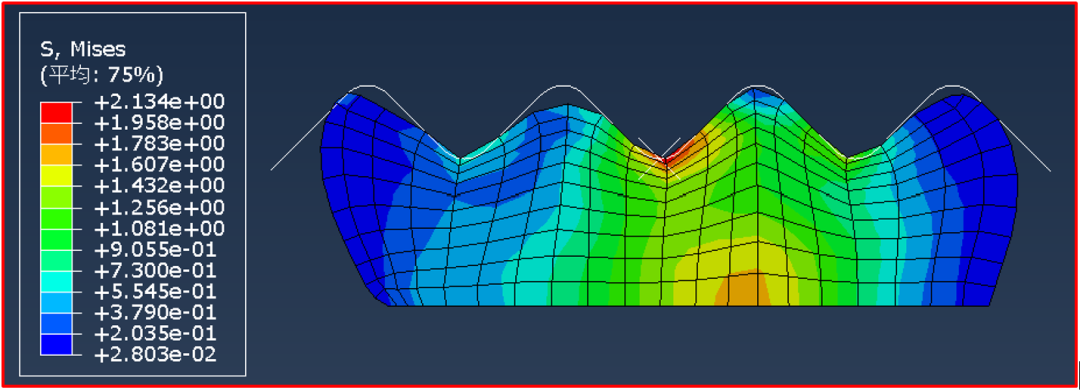
图12 有ALE时的结果显示
为了对比有无ALE自适应网格划分技术的计算效果,取消ALE设置,再计算一遍,结果如图13。
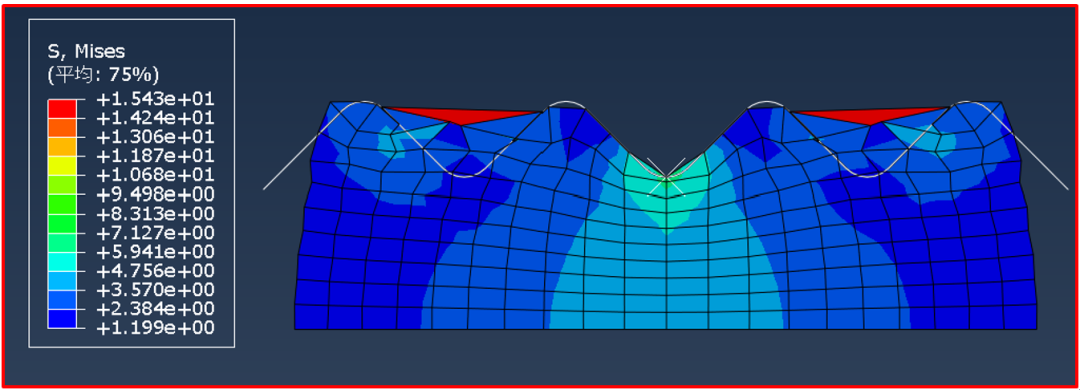
图13 无ALE时的结果显示
从图13中可知,若取消了ALE自适应网格划分,在模具积压橡胶坯件的过程中,有些单元发生畸变,无法 正常显示网格变形,计算结果是不可靠。





