有限元方法中的数值技术：列主元高斯消元法

高斯消元过程中如果在消去过程中出现 0 主元或者是主元非常小的话，消去法将失败或者数值不稳定。这时可以采用选主元的方法，进行处理。

计算原理

1. 设置增广矩阵       
2. 对        至       ，做3~6处理
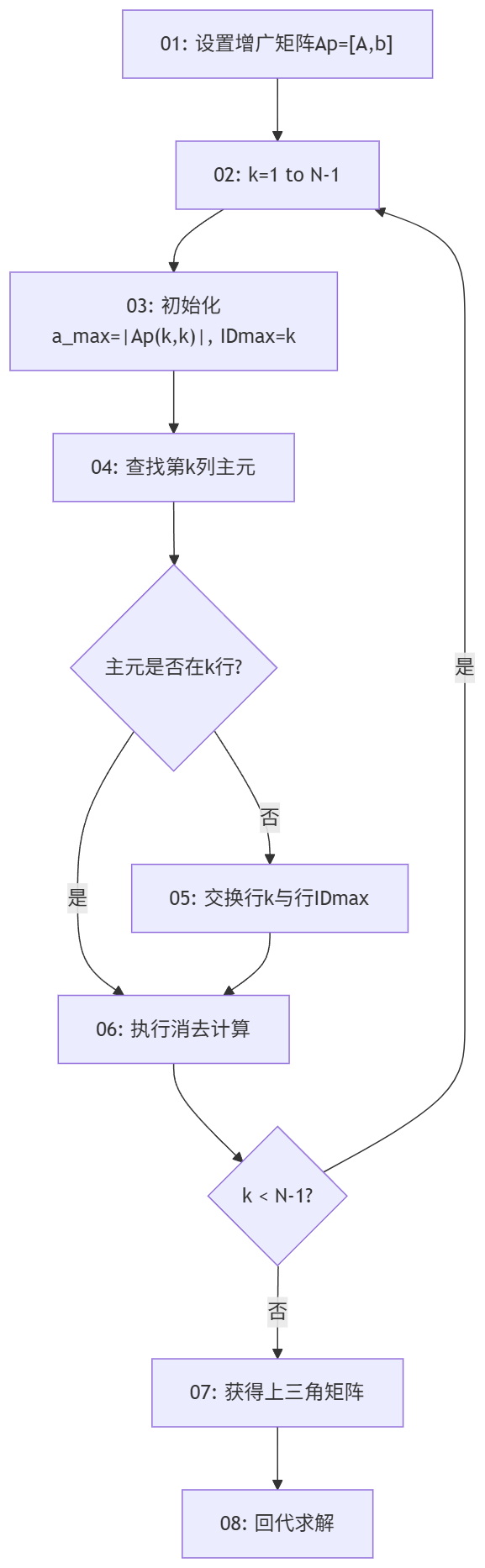
3. 设置一个元素       ，及标号       
4. 查找当列的最大元素，然后用标号        记录下这个元素所在的行数
5. 交换第        行与第        行的所有数据。其他元素保持不变
6. 完成5时已经完成了主元的选取，这时候可以按照上一节的消去法进行消去计算
7. 完成以上步骤之后，已经形成上三角矩阵
8. 对上三角矩阵进行回代，即可得到方程的解

Fortran数值实现

subroutine m_gauss(a,b,x,n)
! 列主元高斯消元法求解线性方程组
integer, intent(in) :: n
real*8, intent(in) :: a(n,n),b(n)
real*8, intent(out) :: x(n)

integer :: i,k,j
integer :: id_max ! 列主元对应的标号
real*8 :: a_up(n,n),b_up(n)
real*8 :: ab(n,n+1)
real*8 :: vtemp1(n+1), vtemp2(n+1)
 ab(1:n,1:n) = a
 ab(:,n+1) = b

!选主元
do k = 1,n-1
  elmax = dabs(ab(k,k)) ! dabs()计算双精度浮点数的绝对值
  id_max = k
! 寻找最大元素对应的标号
do i =k+1,n
   if (dabs(ab(i,k))>elmax) then
    elmax=Ab(i,k)
    id_max = i
   endif
enddo
! 与第k行进行交换
  vtemp1 = ab(k,:)
  vtemp2 = ab(id_max,:)

  ab(k,:) = vtemp2
  ab(id_max,:) = vtemp1
! 交换完毕，进行消元
do i = k+1,n
   temp = ab(i,k)/ab(k,k)
   ab(i,:) = ab(i,:) - temp*ab(k,:)
enddo
enddo

! 打印ab，此时已经变换为上三角矩阵
print *, 'Augmented matrix [A|b] after elimination:'
do i = 1, n
print'(7F12.6)', (ab(i,j), j = 1, n+1)
enddo

 a_up(:,:) = ab(:,1:n)
 b_up(:) = ab(:,n+1)

call uptri(a_up,b_up,x,n)

endsubroutine m_gauss

数值案例

主程序：

program main
    implicitnone
    integer, parameter :: n = 6
    real*8 :: a(n,n), b(n), x(n)
    integer :: i
    
    ! 初始化矩阵A和向量b
    a = reshape([ &
        -3.3435d0, -0.4946d0,  0.3834d0, -4.9537d0, -2.4013d0, -3.5446d0, &
         1.0198d0, -4.1618d0,  4.9613d0,  2.7491d0,  3.0007d0, -3.6393d0, &
        -2.3703d0, -2.7102d0, -4.2182d0,  3.1730d0, -0.6859d0,  3.6929d0, &
         1.5408d0,  4.1334d0, -0.5732d0,  3.6869d0,  4.1065d0,  0.7970d0, &
         1.8921d0, -3.4762d0, -3.9335d0, -4.1556d0, -3.1815d0,  0.4986d0, &
         2.4815d0,  3.2582d0,  4.6190d0, -1.0022d0, -2.3620d0, -3.5505d0  &
    ], shape(a), order=[2,1])
    
    b = [9.0537d0,  0.0228d0, -8.4177d0, -4.6380d0, 10.5575d0, 9.8252d0]
    
    ! 调用高斯消元法求解
    call m_gauss(a, b, x, n)

    print *, "x:"
    do i = 1, n
        write(*, 100) "x(", i, ") = ", x(i)
    enddo

100format(1x, A, I1, A, F10.6)
endprogram main

输出：

 x:
 x(1) =   1.265159
 x(2) =   0.110264
 x(3) =  -1.245209
 x(4) =  -0.433799
 x(5) =  -0.990933
 x(6) =  -2.620118

 

注意：子程序中默认：implicit real*8(a-z)

参考文献

1. 宋叶志,茅永兴,赵秀杰.Fortran 95/2003科学计算与工程[M].清华大学出版社,2011.