接触基础知识:接触计算中的penalty(罚函数)方法
有限元接触分析中的罚函数法(Penalty Method)是一种广泛应用的数值算法,说罚函数大家可能不一定立刻理解,但其实可以理解成一根根非常硬的弹簧用以强制满足接触界面的非穿透条件。以下从基本原理、算法实现、优缺点、应用场景及参数设置等方面进行全面解析:
一、基本思想与数学模型
罚函数法假设接触面间存在虚拟弹簧。当发生穿透时,弹簧产生抵抗力:
其中:
为接触压力(法向力), 为接触刚度(惩罚因子), 为穿透量(接触面嵌入深度)。
理论上,当 时穿透量 ,但实际因为我们进行的是数值计算而不是理论计算, 不可能取无穷大,所以就都会有些小的穿透,就看穿透多大大家能接受了。其实上述的一切就是为了用一些个比较硬的“弹簧”保证“不会有穿透的发生”。
二、数值实现特征
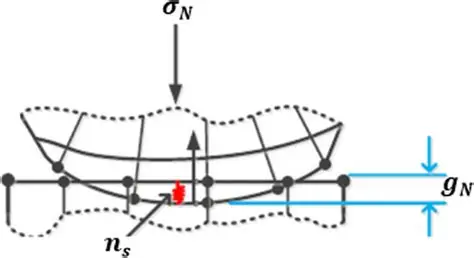
一般来说对于点对面的方法有两种实现方式,一种是在单元节点上进行检测、另外一种是在积分点处进行检测,就以最简单的节点处进行检测为例,对于从面的节点,进行该节点到主面的投影(住从面的网格大概率不一致),得到投影点的坐标,进而反向求得该点的参数坐标,那么穿透量就可以由以下的公式计算得到
这里是以2D下的接触为例,其中点1,2为投影的主面(一条边)上的两个节点。然后就可以计算接触力
也就建立了接触力与主面从面相应节点的位移之间的关系,非常的简单直接,也不用引入新的自由度!如果是显式计算到这基本上就完了,如果是隐式计算还需要计算切线刚度矩阵,这个对于大小滑移还有点不一样,后续再详述。
上面说的是法向的接触力,其实切向一样也是选用个罚函数因子,然后计算切向的摩擦力,
不过不同的点在于这里切向的力未必是对的,只是先“试一下”,所以叫做试切向力,因为其并不一定满足摩擦力的基本原则:
其中 为摩擦因子。
三、技术优势与局限
下面讨论下penalty接触的适用性:
| 优势 | 局限性 |
|---|---|
| 计算效率高 | 精度依赖参数 |
| 收敛性好 | 无法消除穿透 |
| 通用性强 | 摩擦模型简化 |
最后令开发者和使用者最烦恼的往往就是总是需要调整罚因子,去得到不同材料、不同接触情况下稳定的收敛和精确的结果,很多人写过一些自适应的调整罚函数因子的方法,但往往只在某个领域好用,稍微换一个另外的领域(比如你模拟金属接触,我模拟橡胶接触)这些建议的penalty因子往往取不到比较好的效果,这个时候就有引入拉格朗日算子法(LM),与ALM方法的必要,这个且听下回分解。





