CFD|基于CFD 方法的景区人行悬索桥气动特性研究-上
本研究采用CFD 软件midas NFX 对特定景区人行悬索桥进行数值模拟,深入探究了该悬索桥主梁的气动特性及涡激共振现象,分析了影响主梁三分力系数、涡脱频率和涡激共振起振风速的因素及其机理。
桥梁涡激共振
桥梁涡激共振作为一种典型的流体-结构相互作用现象,历来是桥梁工程和流体力学研究领域的重要课题。大幅度的涡激共振不仅会引起不适,还可能影响行车安全和结构的疲劳性能。因此,深入理解涡激共振的机理、预测其发生条件以及探索有效的控制策略,对确保大跨度桥梁的设计安全和运营稳定具有重要意义。
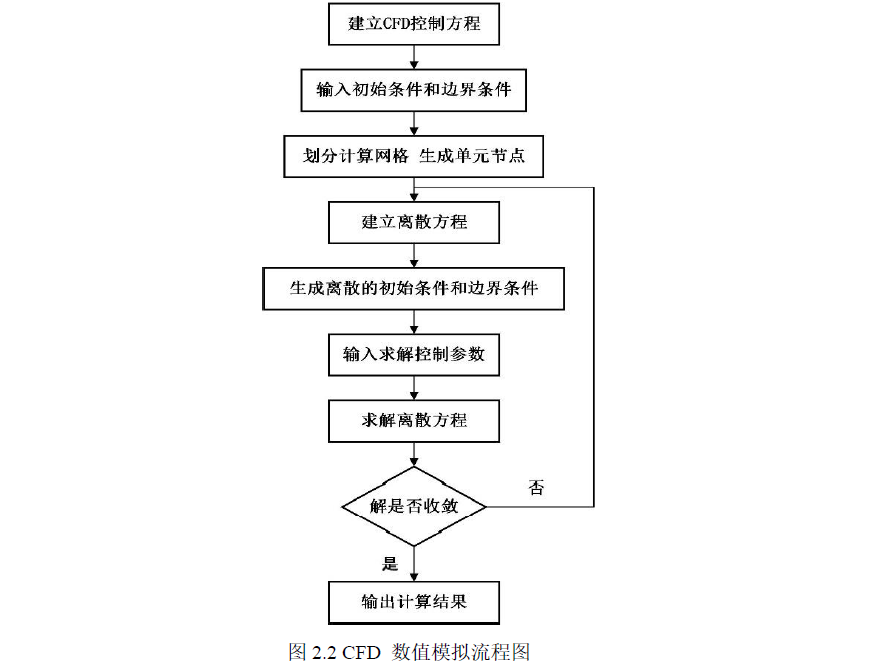
CFD 的数值求解步骤
网格生成:在计算域内生成网格,用以划分流体流动区域。
方程离散化:将连续的流体动力学方程转换为离散方程,以便在每个网格单元上进行数值求解。常用的离散化方法包括
有限差分法(Finite Difference Method)
有限体积法(Finite Volume Method)
有限元法(Finite Element Method)
边界条件和初始条件的设定:根据实际问题设定适当的边界条件(如流体速度、压力、温度等)和初始条件。
数值求解:使用迭代方法求解离散方程组,得到流体在各个网格单元的速度、压力和其他相关物理量。
结果后处理和分析:对计算得到的数据进行处理和分析,以得到流体流动的详细信息,如速度场、压力场、温度场等。
midas NFX 介绍
midas NFX 是MIDAS IT 公司开发的一款多物理场仿真和优化设计软件,基于有限元方法原理。它提供了一个全中文的用户友好界面,将结构、热、流体分析集于一体,支持多种分析类型,包括线性和非线性静力分析、模态和屈曲分析、热传递和热应力分析、线性和非线性动力学分析、多体动力学分析、疲劳分析、复合材料分析、优化设计(拓扑和尺寸优化)以及CFD分析。
软件具有工作界面友好、支持多种单元混合模型(如实体、壳、框架等)、计算准确快速、结果可靠等优点,适用于各类工程设计和分析需求。特别是在21 世纪,产品设计的分析需求已经从单一物理场过渡到多物理场综合分析,从强度校核过渡到疲劳寿命分析,从分析校核过渡到优化设计,从单一柔性分析过渡到刚柔耦合分析。midas NFX 正是为顺应这些需求而提供的一个仿真分析驱动的设计平台。
软件还涵盖结构、温度、流体及它们之间的相互关系分析,提供 产品分析的整体解决方案。它还支持CPU 和GPU 的高性能并行计算,能够处理复杂的多物理场问题,特别适用于需要精确模拟和分析的高端工程领域。例如,在桥梁风致振动研究中,midas NFX 可以用于分析桥梁结构在风荷载作用下的动态响应,帮助工程师评估和优化桥梁设计,确保其安全性和稳定性。
总的来说,midas NFX 是一个强大的工程仿真工具,它提供了一套全面的解决方案,能够应对各种工程分析和设计挑战。无论是在结构、热、还是流体分析领域,midas NFX都能提供高效、准确的分析结果,帮助工程师、设计师以及科研工作者在产品开发的各个阶段做出更好的决策。
静力三分力系数数值模拟算例
本章首先将参考文献中描述的人行悬索桥主梁断面模型作为基准,使用midas NFX软件进行静力三分力系数的数值计算。随后,将所得模拟结果与文献中的数据进行对比分析,以此验证数值模拟在本研究中应用的可靠性和准确性。
桥梁主梁断面截取自于某景区山谷上的人行悬索桥,该悬索桥与本文研究的桥型一致,桥系结构相似。文献截取的主梁断面之一如图3.3 所示,主梁纵梁采用工字钢130c,未设置风嘴。主梁断面高度为0.35m,宽度为2.43m

midas NFX 数值模拟过程
(1)建立模型
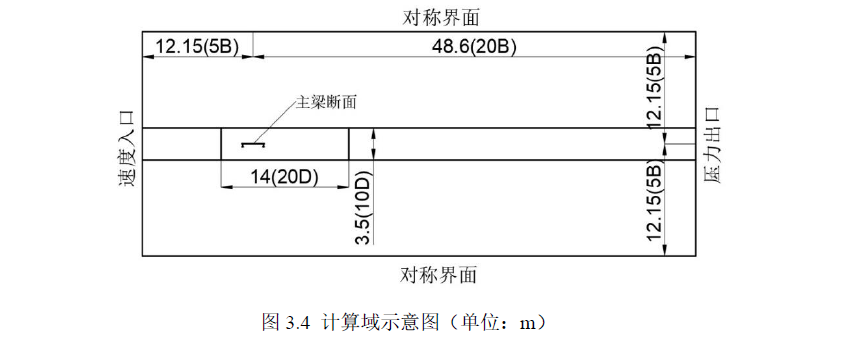
在CAD 中建立文献中描述的悬索桥主梁断面的二维几何模型,并建立风场计算区域,在符合《公路桥梁抗风设计规范》要求的前提下,对文献的风场计算区域进行缩小处理。如图3.4 所示,为提高运算的速度与精度,网格划分时,将风场计算区域分块,近壁面区域宽14m,高3.5 米。风场计算区域中,左侧速度入口距离主梁断面中心为5B,即12.15m;右侧压力出口距离主梁断面中心为20B,即48.6m;上下对称边界距离主梁断面中心为5B,即12.15m。风场计算区域总宽度为60.75m,总高度为24.3m,总面积为1476.225m2。根据阻塞度公式(3-11),在2D 平面内,建筑物最大迎风面积转化为主梁断面高度,同理,计算区域横截面积转化为此风场计算域的高度,经计算,此风场计算域阻塞度为1.4%,符合《公路桥梁抗风设计规范》计算域阻塞度不得低于3%的规定。最后将CAD 二维线框文件导入midas NFX 软件,并生成面域。

(2)定义材料及特性
1)定义材料
midas NFX 提供了众多材料,并给出了各材料相应的特性指数。选择AIR-25℃,流体为不可压缩模型,质量密度为1.11845kg/m³,空气属牛顿流体,流体粘度为1.8444×10⁻⁵kg/(m·s)。
2)定义单位特性
添加单元特性CFD 2D 类型,赋值予前文定义的AIR-25℃,材料坐标系为总体直角坐标系。
(3)划分网格
有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素[64]。从几何表达上讲,平面应力和平面应变情况设计的单元求解方程也不相同。在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同。
在本文中,有限元网格的划分被认为是影响数值计算分析结果精度的关键因素。通常情况下,网格越细密,计算结果越接近真实情况,尤其是靠近主梁断面的网格对数值模拟的精确性有显著影响。为了平衡计算机的运算效率和模拟结果的准确度,本研究将风场计算区域划分为近壁面区域和外围区域。其中,近壁面区域的网格密度高于外围区域,并对靠近壁面的区域进行进一步的网格加密处理。如图3.5(a)所示,为了更直观地展示网格划分情况,选择了第二种网格划分方案的模型进行示意,图中绿色部分代表近壁面区域网格,黄色部分代表外围区域网格。具体措施如下:
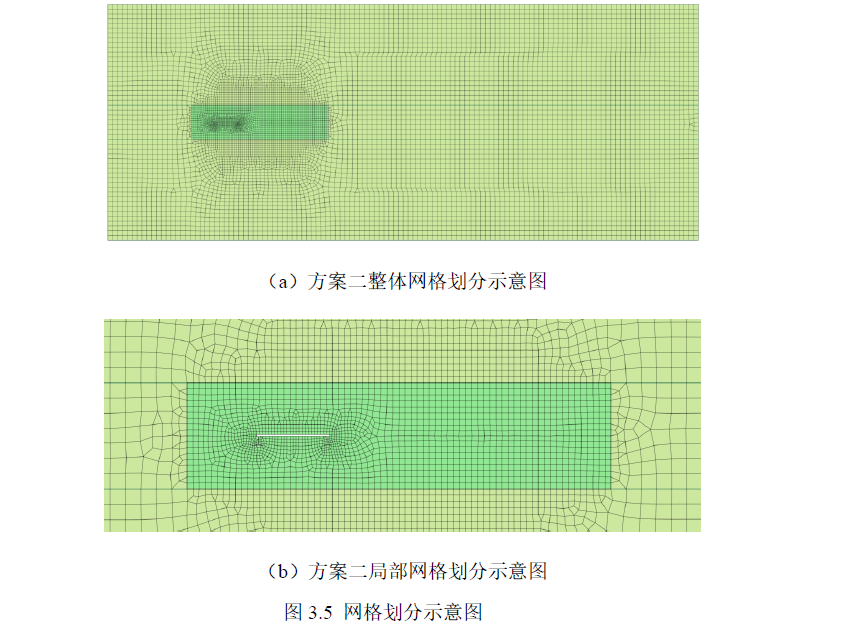
1)壁面处网格尺寸小于近壁面区域网格尺寸,如图3.5(b);
2)近壁面区域边界网格尺寸小于外围区域网格尺寸,且近壁面区域边界网格尺寸与近壁面区域网格尺寸相等如图3.5(b);
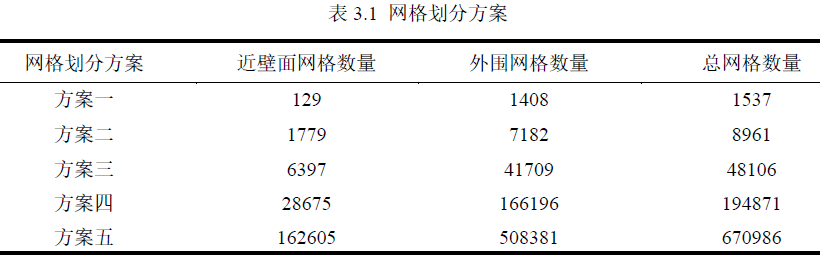
3)为验证网格密度与主梁断面的数值模拟计算结果精度的关系,如表3.1 所示,本文给出五种网格划分方案。
(4)定义边界条件
对于风场计算域来说,通常定义主梁断面的壁面边界及风场区域四周的边界为模型的计边界。如图3.4 所示,风场计算区域的左侧定义为速度入口,入口风速为7m/s;风场计算区域的右侧定义为压力出口,默认压力数值为0,即大气压;风场计算区域的上下对称边界定义为速度边界,速度与入口风速一致,为7m/s;主梁断面边界定义为无因次距离壁面(y+)边界,第一个节点y+或y 的数值为软件默认值65
(5)求解
CFD 分析环节中,求解类型选择稳态CFD,分析控制界面,模块默认为流体流动。因求解类型为稳态求解,故分析中的时间增量对结果影响不大,因此,此处按照工程习惯,将时间增量定为0.005 秒,步骤数为4000 步,最大迭代次数为5 次,初始求解步骤为1,每20 步输出一次结果。初始条件中,定义湍流动能和湍流长度尺寸,根据式(3-12)、式(3-13)、式(3-14)及式(3-15)求得湍流动能为0.09447476,湍流长度尺寸为0.0245。湍流模型选择RNG k-Ɛ模型,默认根据体和场进行网格变形。
输出控制界面,选择静压力与速度,并自定义三分力系数公式:阻力系数
 、升力系数
、升力系数 与扭矩系数
与扭矩系数 Moment Coefficient。
Moment Coefficient。

静力三分力系数计算结果
利用CFD 软件midas NFX 对所述模型进行计算后,分别得到五种网格划分方案下的风轴静力三分力系数,即阻力系数 、升力系数
、升力系数 与扭矩系数
与扭矩系数 ,并与文献的结果进行对比。如表3-2所示,(表中差值指本文求得的静力三分力系数与文献三分力系数的差值的绝对值)。得出一下结论:
,并与文献的结果进行对比。如表3-2所示,(表中差值指本文求得的静力三分力系数与文献三分力系数的差值的绝对值)。得出一下结论:
(1)本研究发现,当计算区域近壁面网格和外围网格数量较少时,得到的静力三分力系数与文献结果相差较大;但随着网格数量的增加,这一差异逐渐减小;
(2)本研究中的方案四得到的静力三分力系数与文献结果的差异最小,表明方案四的网格划分方式与文献中的类似;
(3)通过以上分析,验证了CFD 软件midas NFX 在模拟主梁断面在风场中的状态及静力三分力计算中的准确性和可靠性,为本文后续研究的准确性提供了有力的保障
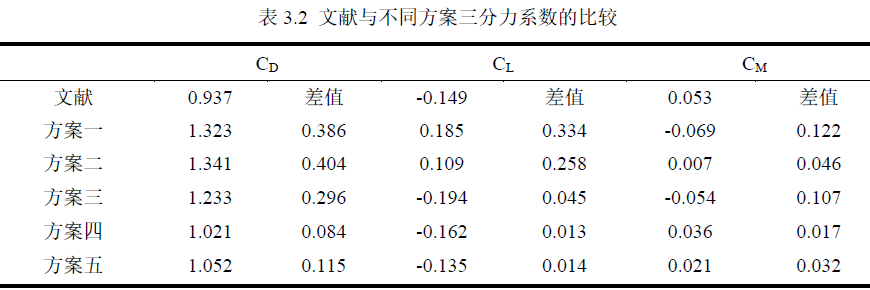
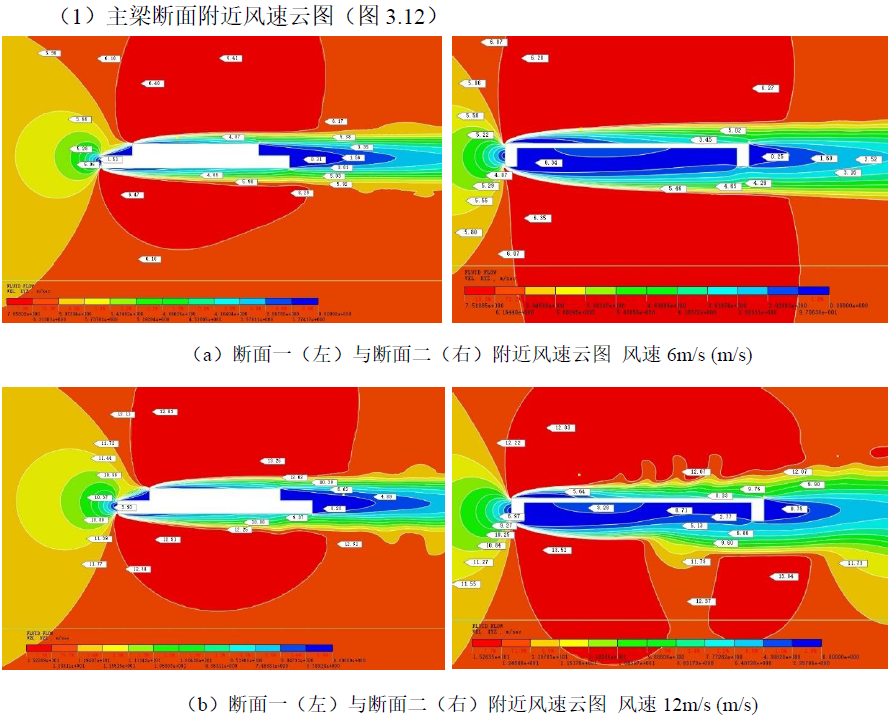
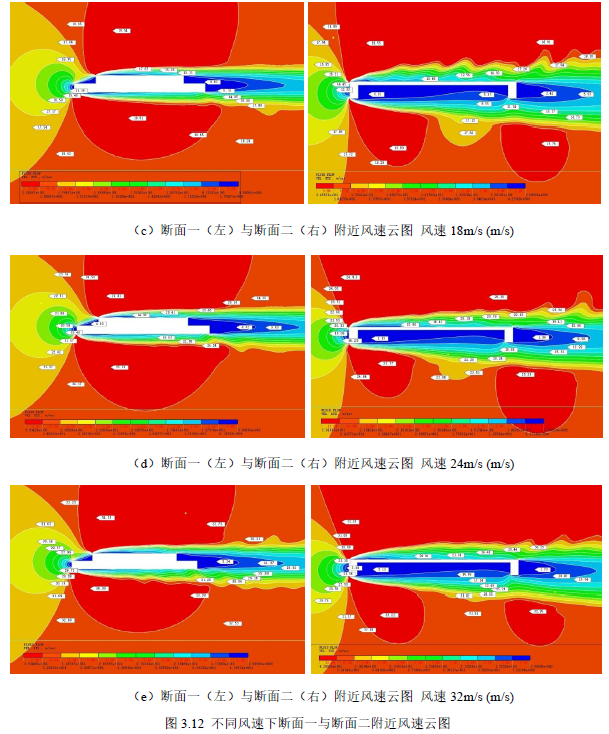
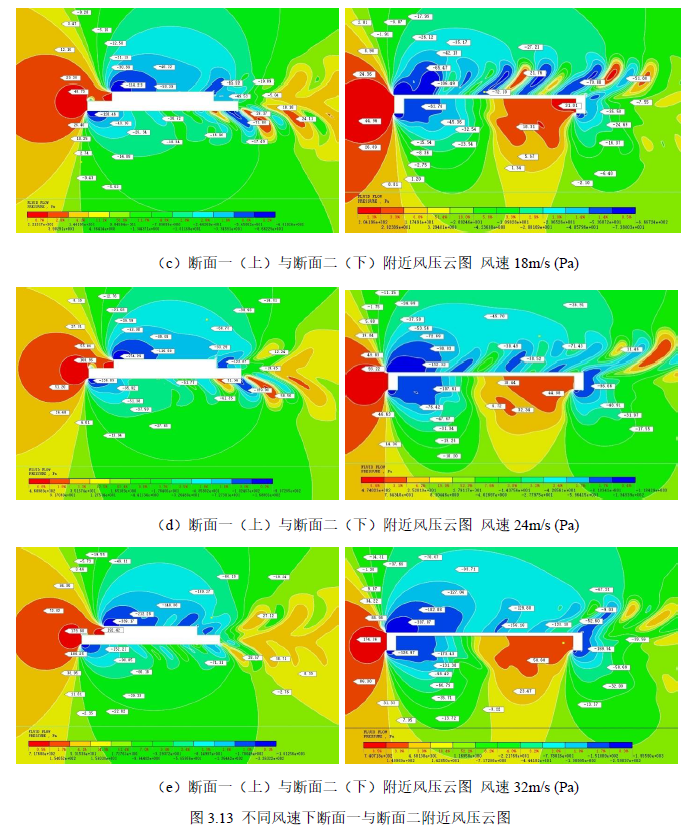
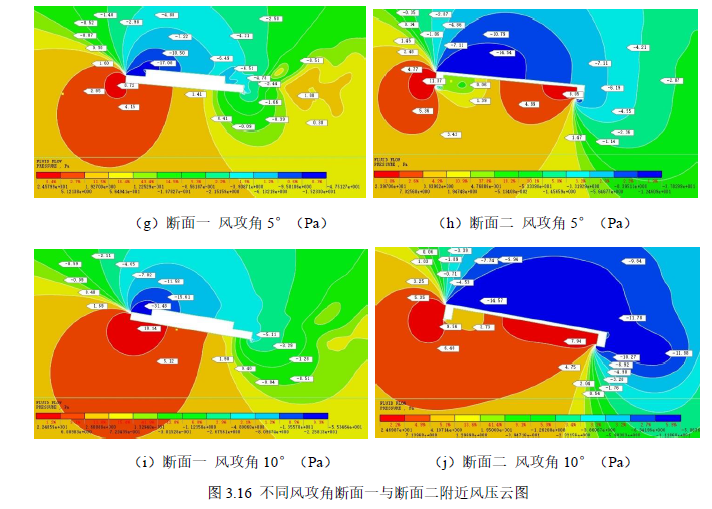
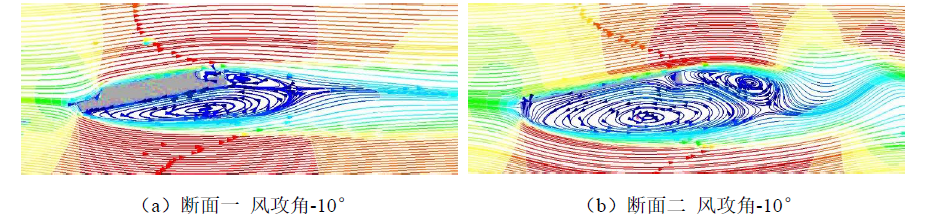
通过仿真模拟生成的主梁断面附近的风速云图和风压云图来分析不同风速对主梁静力气动特性产生影响的具体原因。所有风速工况均选取模型计算的第2001 步(即中间步)作为分析的基准点,以确保分析的一致性和可靠性。
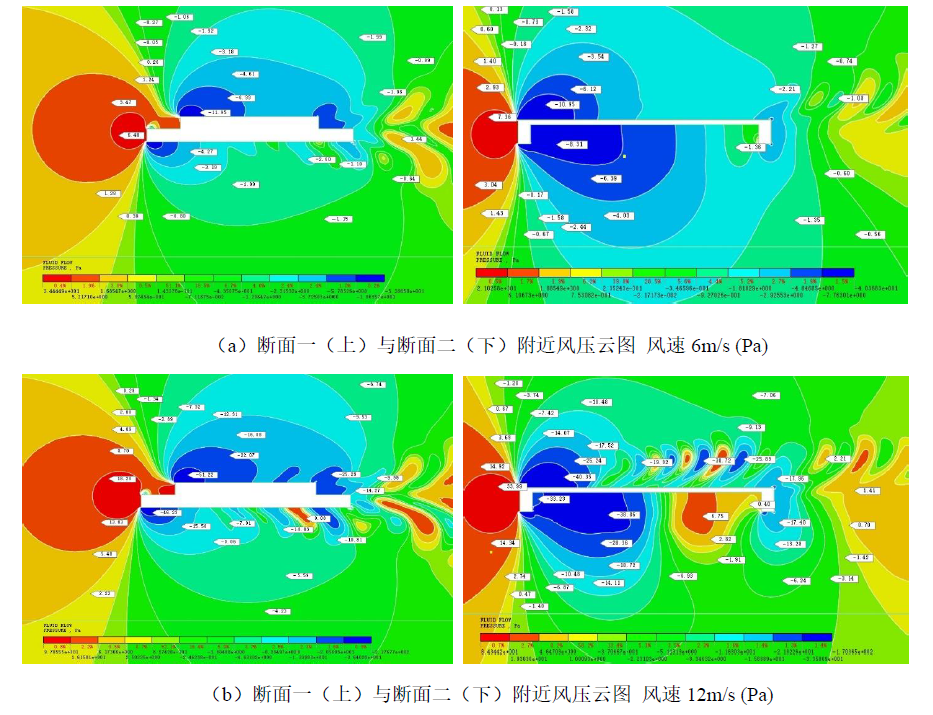
主梁断面附近风压云图(图3.13)
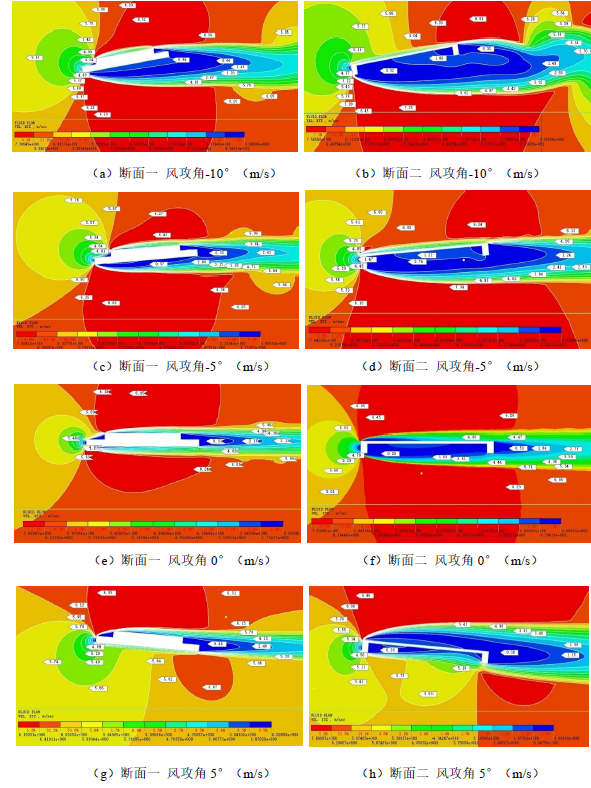
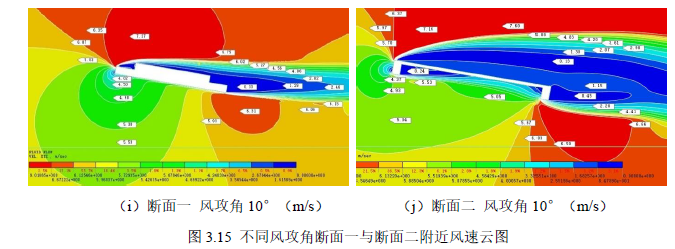
主梁断面附近风速云图(图3.15)
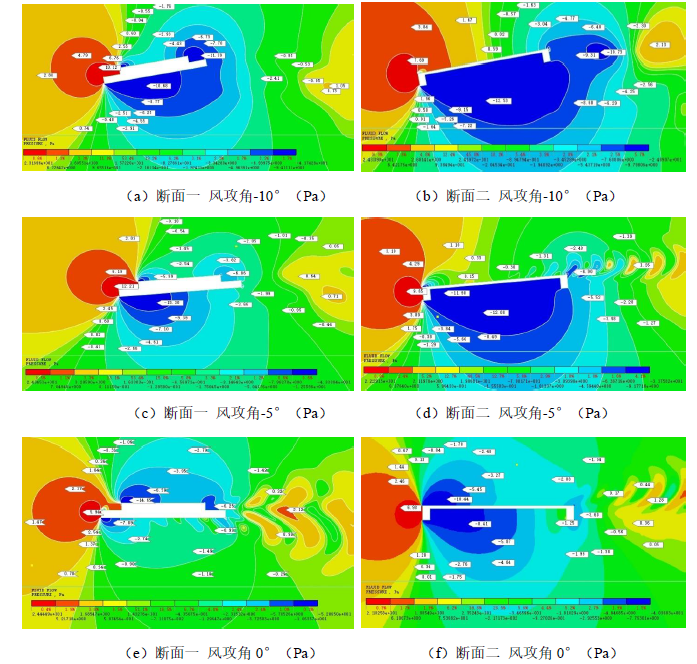
主梁断面附近风压云图(图3.16)
主梁断面附近来风流线图(图3.17)

本章小结
本章主要探讨了景区人行悬索桥主梁的静力气动特性,包括静力三分力系数的求解过程,以及风速、风攻角和断面风嘴对静力气动特性的影响,并分析其机理。
首先介绍了静风荷载的形成,根本原理是伯努利原理。据此推导出静力三分力系数,包括风轴静力三分力系数和体轴静力三分力系数,以及它们之间的转换关系。
为了验证CFD 软件midas NFX 的计算准确性,本研究选取了文献中的模型进行对比分析,发现结果与文献模拟结果基本一致,且网格越密,结果越精确。这为后续的数值模拟研究提供了可靠保障。
接着,本研究基于实际工程建立了简化模型,并以静力三分力系数为核心,分析了风速、风攻角和风嘴对主梁静力气动特性的影响。具体分析如下:
(1)总体来说,静力三分力系数随风速增加而增大,但变化不明显,尤其是扭矩系数。这是因为随着风速增加,断面迎风侧与背风侧的压力差及上下侧压力差均成平方增加,而静力三分力系数公式中的风速增速也成平方增加,导致静力三分力系数变化不显著。
(2)随着风攻角增大,主梁断面的升力系数和扭矩系数呈增大趋势,而阻力系数先减小后增大,最小值出现在0°风攻角附近。这是因为主梁断面改变了其附近的气流形态,导致断面迎风侧与背风侧风压差、上下侧风压差发生相应变化,进而影响阻力荷载、升力荷载和扭矩荷载。
(3)风嘴的引入可以有效降低主梁断面的阻力系数,其中圆风嘴的效果最显著,但可能会小幅增加升力系数和扭矩系数。综合考虑,圆风嘴在降低静力三分力系数方面表现最佳,因为它能引导气流顺畅流过主梁断面,减少气流分离再附着现象。
(4)通过比较断面一和断面二,发现规则断面的静力三分力系数较低。这是因为规则断面对流经其附近的气流影响较小,导致断面左右侧及上下侧的气压差较小。
作者:
彭 一
文章摘自
硕士专业学位论文
《基于CFD 方法的景区人行悬索桥气动特性研究》





