自适应收敛可视化图神经网络 | ACVGN:一种可解释的智能滚动轴承故障诊断方法
论文基本信息
论文题目:
Adaptive Convergent Visibility Graph Network: An interpretable method for intelligent rolling bearing diagnosis
论文期刊:Mechanical Systems and Signal Processing
论文日期:2025年
论文链接:
https://www.sciencedirect.com/science/article/pii/S0888327024006599
作者:Xinming Li (a), Yanxue Wang (a,b), Shuangchen Zhao (c), Jiachi Yao (a,b), Meng Li (a)
机构:
a: School of Mechanical-Electronic and Vehicle Engineering, Beijing University of Civil Engineering and Architecture, Beijing, 100044, China;
b: Beijing Key Laboratory of Performance Guarantee on Urban Rail Transit Vehicles, Beijing University of Civil Engineering and Architecture, Beijing, 100044, China;
c: College of Education, Capital Normal University, Beijing, 100048, China
团队带头人简介:王衍学教授,北京建筑大学机电与车辆工程学院执行院长,博士生导师,入选北京市百千万人才工程,青年北京学者,德国洪堡学者,广西海外高层次人才计划,主要从事机械系统动力学建模分析、动态信号处理与特征提取、装备故障自诊断与智能维护、剩余寿命预测与健康管理、无损检测与嵌入式系统方向的研究工作。主持包括5项国家自然科学基金,德国洪堡基金,广西自然科学杰出青年基金等在内的多项省部级以上课题10余项。(来源: https://jdxy.bucea.edu.cn/dtxw/6674668781d94e2da33d81f463730fac.htm)
目录
1 摘要
2 引言
3 相关研究内容
3.1 图神经网络
3.2 时间序列数据的图表示构建
4 所提方法
4.1 ACVG算法
4.2 具有可微分池化机制的图分类模型
4.3 ACVGN算法
4.4 基于ACVGN的智能机械故障诊断框架
5 实验验证
5.2 数据集预处理
5.3 实验分析
6 结论
1 摘要
在机械设备维护领域,故障诊断的高效性和准确性至关重要。传统的图神经网络(GNN)方法已被应用于利用时间序列数据进行故障诊断,并取得了一定效果,但仍存在不足。这些方法的主要问题在于将时间序列数据映射为图数据,通常会导致重要的时间信息丢失,且计算效率较低。这些局限性可能导致诊断结果不尽如人意,从而影响机械系统的使用寿命和整体性能。
为克服这些问题,提出了一种新的端到端智能诊断框架——ACVGN,该框架结合了自适应收敛可视化图(Adaptive Convergent Visibility Graph Network, ACVG)算法与增强版DiffPool模型的优势。ACVG算法作为该方法的核心,通过巧妙地将时间序列数据转化为图格式,能够有效地保留数据中的局部和全局动态信息。该表示随后由改进后的DiffPool模型处理,该模型专为高精度分类任务设计,并具备强大的GNN能力。实验结果表明,在广泛应用的滚动轴承数据集上,ACVGN框架在图数据映射效率和故障诊断准确性方面均显著优于现有方法。上述成果不仅验证了所提方法的有效性,还突显了其在涉及时间序列数据分析和图基机器学习任务中的潜在应用前景。本研究推动了更智能、高效、精确的机械设备诊断工具的发展,确保了故障检测和诊断的有效性,从而有望延长机械系统的使用寿命,并提升其整体功能。
关键词:深度学习,智能诊断,图神经网络,自适应收敛可视化图网络,可解释性框架
2 引言
传统机械故障诊断主要依赖操作人员在特征提取与模式识别方面的经验知识,然而,随着人工智能的发展以及深度学习技术的快速进步,智能故障诊断开辟了新的研究路径。
现有的故障诊断方法大致可分为数据驱动方法与物理模型驱动方法。由于机械设备本身的复杂性,基于物理建模的方法在机械设备中的应用受到了较大限制。机械系统所涉及的物理过程通常表现出非线性与动态特性,因此准确建模与预测系统行为具有相当大的挑战性。相较之下,近年来数据驱动方法获得了更广泛的关注。基于数据挖掘的方法可通过多种神经网络架构自动提取故障特征并完成特征分类,例如卷积神经网络(CNN)、循环神经网络(RNN)、长短期记忆网络(LSTM)以及自编码器。这些研究充分展示了数据驱动方法在故障诊断领域中的发展与成效。然而,尽管上述深度学习方法在特征提取和故障分类方面取得了显著进展,但它们普遍忽视了数据样本之间的关联性,从而难以充分挖掘数据所蕴含的结构信息与几何特征。
随着物联网与多种信息感知技术的不断进步,工业系统所产生的数据规模日益庞大,这些数据往往具有非规则空间拓扑特征,例如网络结构与流动模式。监测系统中使用大量传感器采集多通道、多维度的信号,生成大量具有图结构特征的数据。面对这一挑战,近年来兴起了一类基于非规则图结构建模的数据依赖性深度学习方法。图结构作为一种典型的非欧几里得数据表示形式,由节点(样本)与边(关系)组成,能够保留丰富的结构信息。通过构建样本之间的关联图,可以有效刻画样本间的关系。尽管图结构数据具有极高的表达潜力,但传统深度学习模型在处理非欧几里得数据时存在困难,如图 1 所示。在图 1(a) 中,卷积计算以二维或三维张量为输入,采用固定卷积核对欧几里得数据执行卷积操作;而图 1(b) 中的图卷积计算则以节点特征向量为输入,卷积核随节点邻接关系变化,从而能够对非欧几里得数据进行卷积运算。
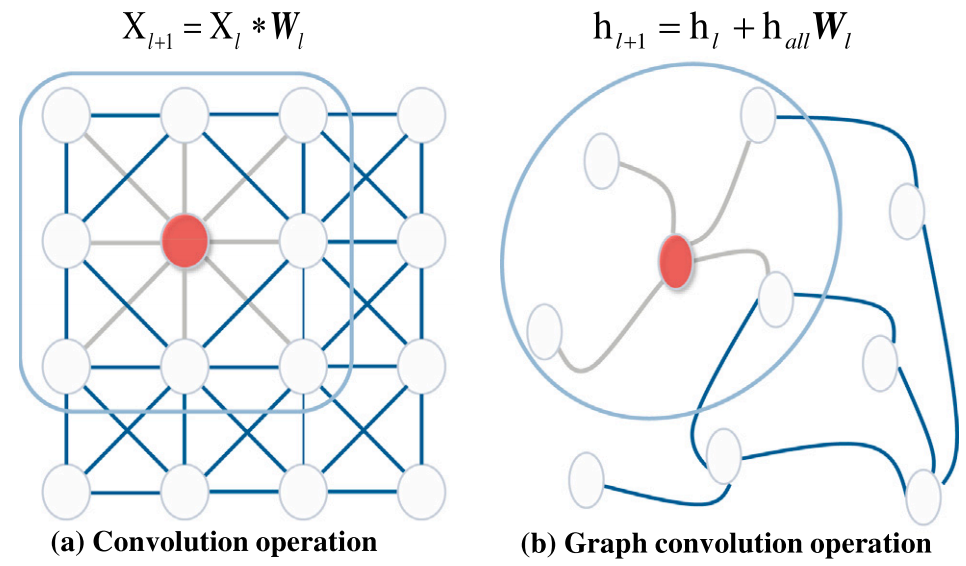
图 1 传统卷积操作与图卷积操作之间的区别
图神经网络(GNNs)在处理图结构数据方面展现出强大的能力,广泛应用于多个领域,大量研究进一步印证了GNN的多样化应用潜力。然而,将时间序列数据高效转换为图数据依然是一项关键挑战。因此,近年来大量研究聚焦于开发高效的图构建方法,并进一步利用GNN架构提升故障诊断性能。
为了将时间序列数据转换为图数据,已有多种技术被提出。这些方法涵盖了基于阈值、相似性、重构以及深度学习的转换策略。尽管相关方法日益丰富,但近年来通过将时间序列数据映射为图结构,并借助GNN进行故障分类的研究方向,被认为具有广阔的发展前景。该领域的首次重要突破是由研究者提出的可视图(Visibility Graph, VG)算法,该方法通过固定映射规则将时间序列转换为图结构。其有效性促使一系列后续优化方法的提出。例如,为应对噪声干扰问题,Gao 等人提出了有限穿透可视图( Limited Penetrable Visibility Graph, LPVG),通过引入不满足可视性标准的有限边,提高了油气水等领域的分类性能。在进一步优化VG算法的趋势下,Xuan等人结合圆形系统与图嵌入技术,提出了圆形有限穿透可视图( Circle Limited Penetrable Visibility Graph, CLPVG),在无线电信号分类任务中取得了优异效果。
在这些可视图及其变体算法中,每一个采样点被视为图中的一个节点,节点间关系依据特定的映射规则构建,如图 2 所示。尽管该类算法为时序图构建领域作出了重要贡献,但它们存在一个共性问题:由于映射规则基本固定,图结构在训练过程中也是固定的。在面对如故障监测数据这类复杂任务时,这种刚性结构限制了模型对复杂动态场景的适应能力。因此,亟需进一步研究能够自适应学习与动态调整的图结构模型。
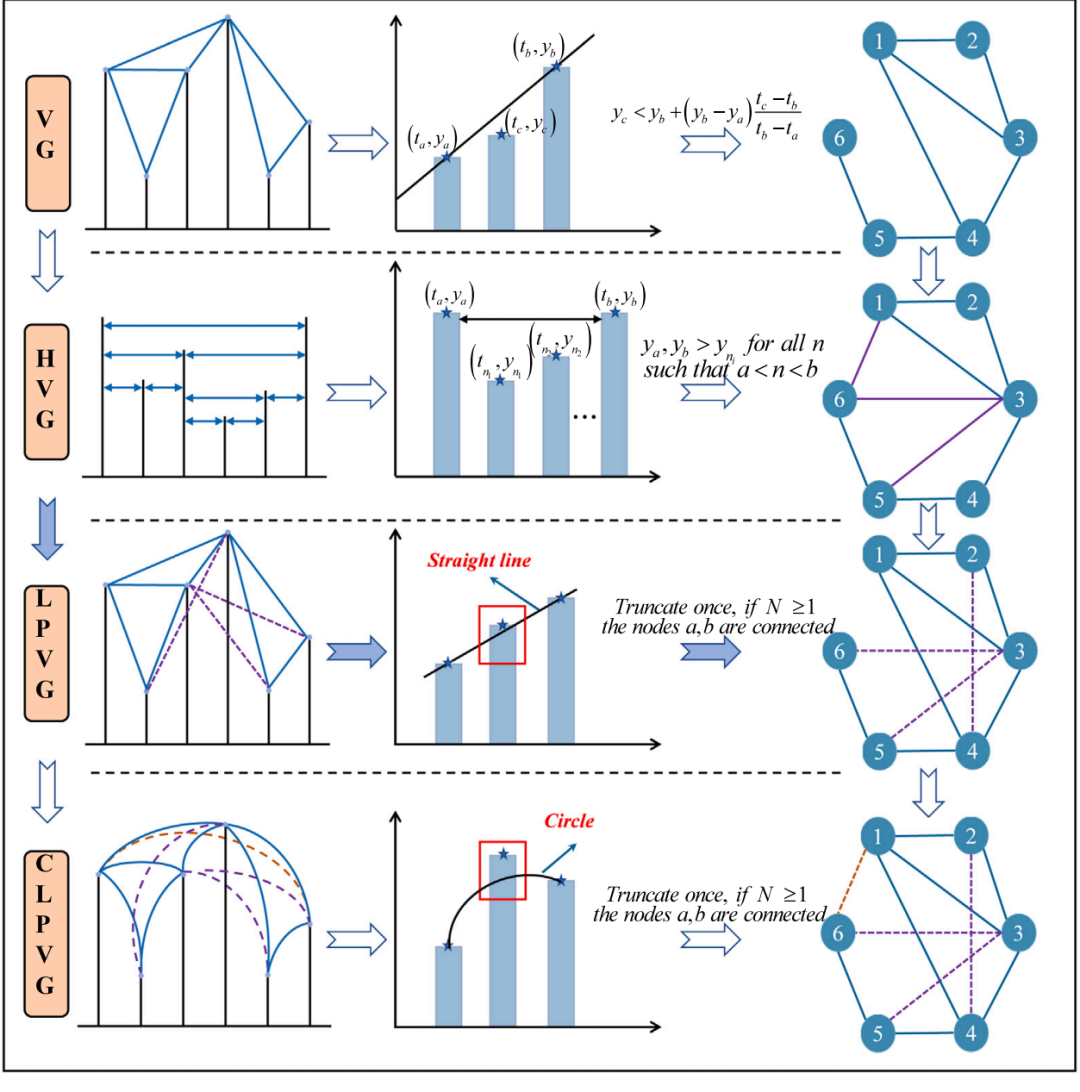
图 2 可视图(VG)及其衍生算法的图映射规则示意图
在当前智能诊断技术的发展中,深度学习模型的可解释性问题已成为关键关注点,尤其是在基于图的分析方法中表现尤为突出。GNN在处理复杂数据集与挖掘深层模式方面具有强大能力,但其模型结构通常被视为“黑箱”,缺乏足够的透明度,使用户难以全面理解并信任其决策过程。因此,近年来研究重点逐渐转向开发既具高精度又具可解释性与可靠性的诊断方法。当前的研究工作主要集中在将可解释性嵌入到模型结构中或通过事后分析技术实现模型解释。这些方法既确保了模型在预测性能方面的有效性,又能够提供与人类专家知识及直观推理相契合的可理解性结果。其中,事前可解释性注重模型结构本身的设计,使模型在建模阶段就具备可分析性与透明性;而事后可解释性则指在模型训练完成后,通过特征重要性评分、偏依赖图(partial dependence plots)以及特征可视化等手段,对其复杂内部机制进行解析。可解释性作为智能诊断方法的基础特性之一,对于推动故障诊断方法的发展,并确保其满足真实工业场景中的高标准应用需求具有重要意义。
本文提出了一种新颖的自适应收敛可视图神经网络框架(ACVGN),用于实现机械设备的智能诊断。这一方法在将时间序列数据映射为图结构的过程中引入了神经网络层级建模,显著提升了结构转换的灵活性与效率。该框架结合了自适应可视图算法与改进型DiffPool结构(后者是GNN中常用的图分类模型)构建了一个完整的端到端智能诊断系统。ACVGN的自适应特性使其能够同时聚合样本的局部与全局信息,从而在分类精度方面表现出显著优势。本研究的主要贡献包括以下几个方面:
首次提出了自适应收敛可视图算法(ACVG)与自适应收敛可视图神经网络框架(ACVGN)。ACVG算法突破了传统可视图算法的局限性,能够动态地将时间序列数据转换为图结构;同时,ACVGN框架充分利用该算法的自适应特性,在显著减少图映射时间的同时,提升了分类精度。
构建了一种面向机械设备的智能诊断框架,该框架将改进型DiffPool技术与自适应可视图算法无缝融合。该创新组合在总体性能方面相较于现有诊断方法有显著提升。
探讨了图学习的可解释性问题,通过对ACVGN映射结果的图结构可视化,深入分析了不同图结构类型之间的差异。这一过程为理解结构差异如何影响机械设备智能诊断任务提供了新的视角与理论支撑。
3 相关研究内容
根据图论,图结构数据可表示为 ,其中 表示节点(或顶点)集 合, 为边集 合, 表示节点 与 之间的边。图 的邻接矩阵 被定义为如下元素组成的矩阵:
因此,在一个具有 个节点的图中,二值邻接矩阵 表示节点 与 之间是否存在边:若节点之间存在边,则 ;反之,则 。除邻接矩阵 外,图结构还可由拉普拉斯矩阵 与度矩阵 表示。这三者之间的关系如图 3 所示。通常,图结构数据还包含一个节点特征矩阵 ,其中 表示节点数量, 为节点特征向量的维度。
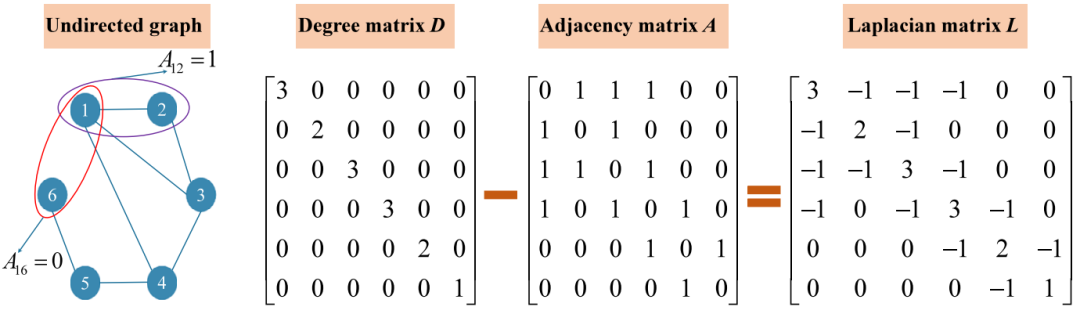
图3 拉普拉斯矩阵的计算
在模型训练过程中,邻接矩阵 与特征矩阵 被作为输入送入GNN,并通过以下公式所示的前向传播过程得到输出结果。在公式中, 表示图神经网络操作, 表示神经网络框架中的层数。
最经典的图神经网络算法之一是图卷积网络(GCN)。受 CNN 的启发,GCN将传统的数据分析方法扩展到图结构数据,通过聚合、更新与循环三个步骤完成特征提取。其核心思想是通过反复聚合某一节点及其邻居节点的特征,生成新的节点表示。节点更新规则如公式所示:
其中, 表示包含自连接的图的邻接矩阵, 为单位矩阵。 表示第 层更新后的节点表示,等同于该层的特征矩阵。第 层的可训练权重矩阵记为 ,而 表示施加于矩阵乘积输出上的非线性激活函数,例如 Sigmoid、ReLU、tanh 等。在GCN中,每一层的计算过程通过将邻接矩阵 与节点表示 相乘得到,每个节点的邻域特征被聚合后,再与权重矩阵 相乘。最终结果经由激活函数 处理,得到新的特征矩阵 ,该矩阵融合了所有邻居节点的特征信息。
本文主要介绍了四种将时间序列数据映射到图结构数据的常用方法。
3.2.1 KNN图(KNN Graph)
若节点 是节点 的 个最近邻之一,则在节点 与 之间建立一条边,从而构成所谓的 -近邻图( -Nearest Neighbor Graph, KNNG)。参数 决定了每个节点的最大邻居数,是影响图结构稠密度的重要超参数。在 维空间中,每个节点的 top- 邻居通常通过其与其他点之间的距离来定义,最常用的度量方法为欧几里得距离(Euclidean distance),其定义如下:
因此,当给定一个 维空间中的点集 时,可以通过计算各节点对之间的距离 ,构建该点集上的 -近邻图(KNNG)。具体做法是将每个点与其 个最近邻连接,以获得节点 的邻居,其表示如下:
其中, 表示节点 的邻居集 合, 表示点集 上节点 的前 个最近邻。本文设置 。
在采用KNNG方法构建图数据时,节点之间所形成的边权重通过高斯核函数(Gaussian kernel function)进行计算,其表达式如下:
其中, 表示节点 与节点 之间的边权重, 为高斯核函数中的带宽参数。需要特别注意的是,在使用高斯核函数计算边权重时,距离 需进行归一化处理,以确保不同维度的特征在距离计算中具有相同的影响力。通过此过程,KNNG可用于构建包含边权信息的邻接矩阵 ,从而实现将时间序列数据 映射为图结构 。
3.2.2 半径图(Radius Graph)
在 算法中,采用余弦相似度(cosine similarity)度量节点之间的距离,以判断两个节点之间是否应建立边连接。第一步是计算点集 中两个节点 与 之间的余弦相似度,其计算公式如下:
其中, 表示节点 与 的点积, 与 分别表示节点 与 的模长, 表示两节点之间的余弦相似度。
为了判断两个节点之间是否存在边连接,假设点集 中任意两个节点 和 的余弦相似度为 ,在给定阈值 的情况下,若 ,则在节点 与 之间建立一条边;否则,不建立连接。由此,节点的邻居可通过以下公式表示:
本文中假设阈值 。需要注意的是,在该算法中,边权重通常并非直接由余弦相似度计算获得。这是因为余弦相似度的取值范围为 ,而边权重一般需定义在区间 内。因此,在算法中,通常需要将余弦相似度值映射至 区间,该映射过程可通过以下方式实现:
其中, 表示将 映射至区间 后的归一化值。最终,节点集 合之间的距离可通过以下公式计算得到:
其中, 表示节点 与 之间的距离,该距离值等价于边权重 。通过上述数据预处理步骤,即可获得带权邻接矩阵 ,从而构建出图结构数据 。
3.2.3 可视图(Visibility Graph, VG)
由 Lacasa 提出的可视图(Visibility Graph, VG)算法,实现了将时间序列数据映射为复杂图结构数据的转换过程。该算法的基本原理是:将离散时间序列中的时间数据点定义为图结构中的节点,若任意两个数据点之间满足可视性准则,则在它们之间建立连接线,作为图中的边。其可视性映射规则可描述如下:
其中, 与 分别表示节点 与 的坐标,任意位于节点 与 之间的数据点的坐标定义为 ,其中时间满足 的条件。
当两个数据点之间的柱顶满足可视性映射规则时,即视为两点之间存在连接。在图结构中,该连接为无向边,节点之间不可自连,且任意两柱状图之间的连线不得穿越其他柱状图。上述映射过程将时间序列数据转换为图神经网络可处理的格式,即图结构数据。
3.2.4 有限穿透可视图(Limited Penetrable Visibility Graph, LPVG)
为提升图构建方法的灵活性,并在将时间序列数据映射为图结构数据时引入更多连接,研究者在VG算法的基础上提出了有限穿透可视图(LPVG)算法。与VG算法的映射规则不同,LPVG引入了一个超参数——有限穿透距离 ,并规定:当节点 与节点 之间的连线被其间最多 个其他柱状图穿越,且 时,视为节点 与节点 之间存在一条可穿透边。该规则意味着节点 与 之间存在一条边,且可确保每个节点至少具有 条边。由于连接性更强,LPVG还表现出更优的抗噪能力。
4 所提方法
本节将详细介绍新颖的时间序列到最优图数据映射算法——自适应收敛可视图神经网络(ACVGN)。此外,针对大规模图数据计算复杂度高的问题,提出了一种改进型DiffPool算法。最终,通过将ACVGN与改进型DiffPool算法相结合,构建了一个创新的端到端图分类智能诊断框架。
4.1 ACVG算法
为解决现有 及其衍生算法在映射灵活性差与映射效率低方面存在的问题,本文首次提出了一种新方法——自适应收敛可视图算法(ACVG)。该算法旨在尽可能保留原始时间序列数据的结构特征,同时提升图构建的效率。ACVG算法通过将时间序列数据转换为图结构,并结合一维卷积算子对图进行训练,从而实现图分类模型的构建,如图 4 所示。具体而言,目标是将给定的时间序列数据映射为由节点与边构成的图 。
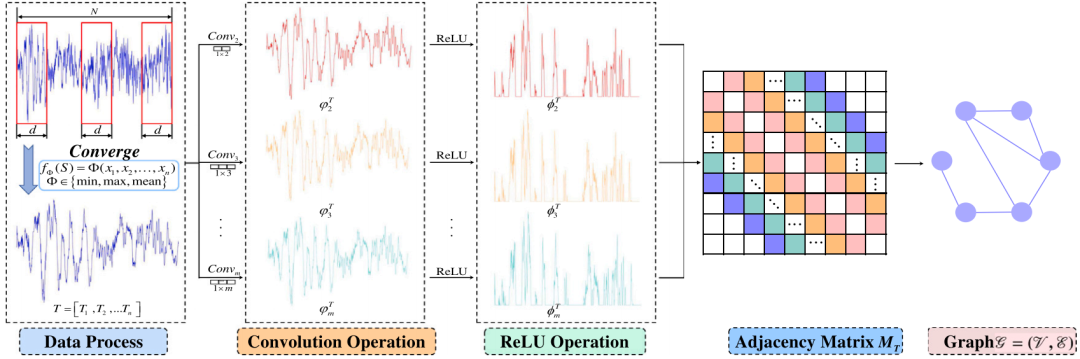
图4 将时间序列数据映射到图结构的ACVG算法
然而,实际采集的时间序列数据通常维度较高,若直接进行图建模将导致计算复杂度显著上升。因此,有必要通过时间窗机制对原始数据进行截断,并对子样本进行聚合,以降低计算负担。这一策略有助于避免信息损失,并提升模型的泛化能力。在ACVG算法的第一步中,长度为 的原始时间序列数据 被划分为多个长度为 的子样本,每个子样本对应一个标签。若任意两个子样本之间无重叠,则该子样本集 合可表示为:
其中, 表示子样本, 表示子样本对应的标签, 为获得的子样本数量, 为每个子样本中的采样点数。所得子样本集 合 随后将进行聚合操作:
假设 表示子样本 中的数据点, 表示聚合函数,该函数可以为最大值、最小值或均值等操作。通过聚合操作后,子样本集 合可表示为:
其中, 表示对子样本 应用聚合函数 所得到的结果;同时, 表示样本点 处的信号值。为了更有效地捕捉时间序列的局部信息与全局动态特征,本文引入了一维卷积算子,该算子采用 个不同的卷积核长度 对结果子集 进行处理。 的特征序列可通过下式获得:
其中, 表示一维卷积层,该层采用长度为 、步长为 1 的卷积核进行操作。超参数 用于控制两个时间采样点之间的距离,从而有助于提取局部信息。通过调整 的取值,可从时间序列数据中提取不同层次的局部信息,进而捕捉数据中存在的多样化模式与特征。
为减弱噪声干扰、提升模型的准确性与性能,本文采用 ReLU 激活函数 对进行处理,该过程可表示为:
最后,通过将经过一维卷积与去噪处理后的特征序列以对角平行方式排列,构建出一个带权的 邻接矩阵 ,从而实现对给定时间序列数据 的图结构映射,生成图 。

其中, 表示连接节点 与节点 之间边的权重。本文提出的ACVG算法通过对子样本的聚合以及借助一维卷积层生成不同复杂度的图结构,有效捕捉了信号值中的局部与全局信息特征。该卷积层充分利用了原始信号值及卷积核长度 ,最终构建出带权邻接矩阵 ,实现了将原始时间序列数据 映射为图的过程。邻接矩阵 是通过对时间跨度敏感的卷积操作动态生成的,它不仅表示节点之间是否存在连接,更基于底层数据模式量化了关系的强度与特征。这种邻接矩阵构建方法,使模型能够捕捉并融合图结构中更为细腻的关系差异,从而为数据动态特征提供更丰富、具解释性的图表示。
4.2 具有可微分池化机制的图分类模型
一旦通过ACVG算法将信号数据映射为图结构后,通常采用图卷积网络(GCN)执行分类任务。然而,在处理大规模图数据时,直接使用GCN会对模型的计算复杂度构成显著挑战。为了解决这一问题,DiffPool算法被提出,作为应对大规模图数据高计算复杂度的可行方案。
DiffPool是一种可微的图池化模块,利用深度图神经网络为每一层节点学习可微分的软聚类分配,将节点映射到一组聚类中。关键在于,DiffPool利用GNN模型的输出学习节点的聚类分配矩阵,使用由GNN生成的第 层嵌入矩阵作为第 层的输入。这使得每个GNN模块能够接收来自前一层的节点嵌入,并聚合特征以生成新的节点嵌入,再传递至下一层,如图 5 所示。
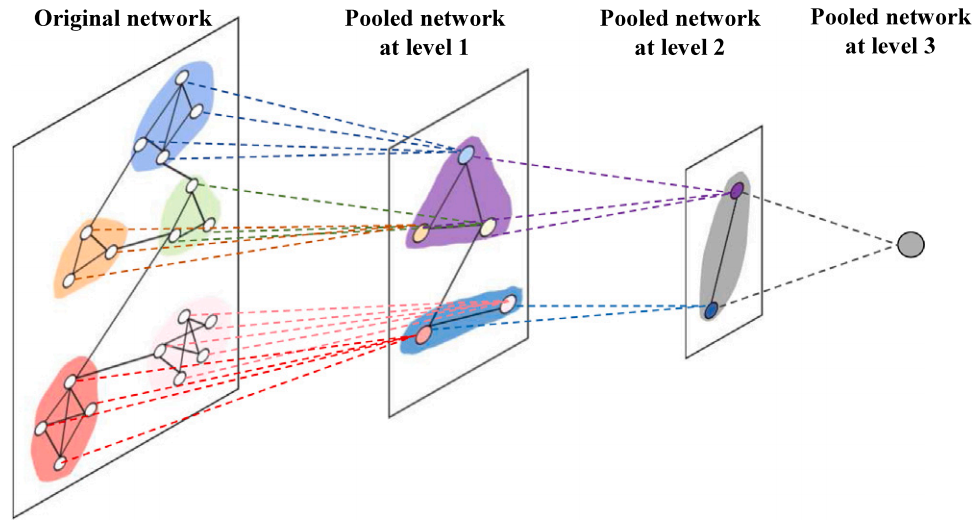
图 5 Diffpool算法示意图
该架构不仅可提取有利于图分类的节点嵌入,还可用于执行图的层次池化,从而实现出色的模型训练性能。假设在第 层学习到的簇分配矩阵表示为 。其中, 的每一行表示第 层中的一个节点 或簇,而每一列对应于下一层 的一个节点簇 。简而言之, 对第 层中的每个节点进行了软分配,将其归属于第 层的一个或多个簇。这种软分配特性使得每个节点可以被分配到多个不同的簇中,从而提供一种更为灵活和细致的图结构表示。DiffPool 的输入定义为 ,其中 表示第 层的邻接矩阵, 表示该层的节点嵌入矩阵。
DiffPool层对输入图进行粗化: 。从而生成新的粗化邻接矩阵 以及粗化图中每个节点或簇的嵌入矩阵 。这通过接下来的两个公式来实现:
矩阵 和 是由两个独立的图神经网络(GNN)生成的,这两个网络分别对输入的邻接矩阵 和簇节点身份矩阵 进行处理。第 层通过嵌入标准的 GNN 模块来计算上述输入:
将邻接矩阵与聚类节点身份矩阵输入至标准 层,得到聚类节点的新嵌入矩阵。同时,通过结合 函数与第 层的池化 进行计算,从而生成聚类分配矩阵:
通过该操作,生成了最终的嵌入向量,该向量表示整个图的全局表示。随后,该全局表示向量被输入至分类器,用于执行图分类任务。
4.3 ACVGN算法
本文的ACVG算法可实现将时间序列数据映射为图数据,并与DiffPool图分类模型结合,构建用于机械设备智能诊断的神经网络架构。该网络利用一维卷积提取数据特征,从而提升映射效率,并取得优异的分类性能。 需要指出的是,该模型除了图的邻接矩阵外,还需为每个节点提供特征向量。对于单通道时间序列数据,可通过ACVG获取邻接矩阵,聚合操作所得的信号值可作为每个节点的特征序列,从而实现ACVG与DiffPool的集成,构建分类网络。对于多通道数据序列,本文以双通道数据为例进行说明,其中两个通道表示如下:
随后,将该特征向量输入至连接层进行分类。由此,构建出一个可用于机械设备故障智能诊断的完整框架,称为ACVGN框架。与现有的VG及其衍生方法相比,ACVG通过卷积与去噪操作,从时间序列中同时提取局部信息与全局特征,进而将故障数据映射为最优图结构,显著提升了模型训练效率。借助该映射技术并结合基于图的分类方法,数据中的时间信息得以完整保留。
4.4 基于ACVGN的智能机械故障诊断框架
图 6 展示了ACVGN模型的整体框架。首先,在机械设备运行过程中,利用加速度传感器采集振动信号。采集到的振动信号被划分为两类:单通道序列数据与多通道序列数据。对于多通道数据 与 ,ACVG算法分别将其映射为图 与 。
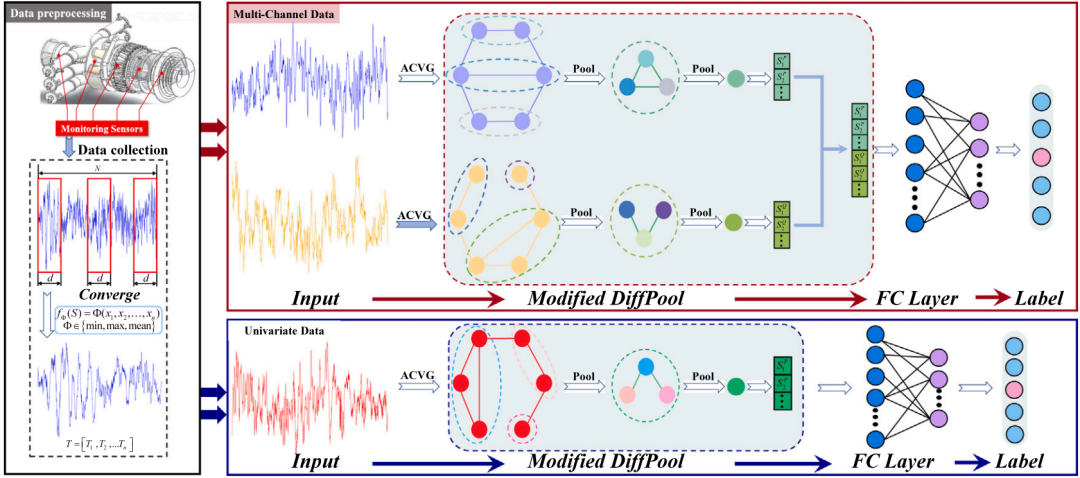
图 6 提出的ACVGN分类框架结构
随后,改进后的DiffPool模型分别处理 与 ,得到对应的特征向量。将这特征向量拼接后生成最终的节点特征向量,并将其输入至全连接层进行处理与分类。对于单通道数据,其处理流程与双通道数据基本一致,唯一区别在于无需进行特征拼接。即:时间序列数据通过 算法转换为图数据,再通过DiffPool获得对应的特征向量,并将其输入至全连接层实现分类。值得注意的是,在模型训练过程中,同时训练图映射过程与图分类过程,以确保所映射构建的图结构更适配原始数据,同时充分挖掘潜在信息,提升模型的图映射速度与分类精度。
5 实验验证
5.1 数据集描述
(1)CWRU 数据集:本研究所采用的第一个数据集为凯斯西储大学故障数据集,该数据集已被广泛用于轴承故障诊断研究中。本研究中选取了缺陷尺寸为 0.1778 mm 与0.5334 mm 的内圈故障、外圈故障与滚动体故障数据子集作为分析对象。
(2)MFPT 数据集:第二个数据集为机械故障预防技术(Mechanical Failure Prevention Technology, MFPT)数据集。其中,前 20 个数据集来自轴承测试平台,包括:3 组正常状态数据、3组恒定载荷下的外圈故障数据、7 组变载荷下的外圈故障数据以及 7 组变载荷下的内圈故障数据;其余 3 组数据来自实际机器,包括:油泵轴承、中速轴承与行星齿轮轴承。在本研究中,选取了其中 13 组工况信号数据:包括1 组正常运行数据、6 组在不同载荷下的外圈故障数据,以及 6 组在不同载荷下的内圈故障数据。实验期间,输入轴转速为 25 Hz,数据采样频率为48,828 Hz。
(3)DIRG_Bearing 数据集:由意大利都灵理工大学的 DIRG 实验室采集,该数据集主要用于高速航空轴承的故障分析,采样频率为 51,200 Hz。实验过程中,研究人员在轴承内圈上人为诱导局部损伤,形成锥形凹陷,根据凹陷直径将其分为 0A(无损)至6A 共七种类型。在本研究中,选取了在轴转速为 200 Hz、两种不同负载条件下采集的振动信号数据,共构成 14 组不同工况的信号数据,用于实验与分析。
(4)XJTU_Gearbox 数据集:该数据集为西安交通大学开源的故障数据集,实验用电机为 3P。实验中故意制造了四种轴承故障状态和四种行星齿轮故障模式。本研究中,选取了四种轴承故障状态的数据集,包括外圈故障、内圈故障、滚动体故障和复合故障,采样频率为 20,480 Hz。
5.2 数据集预处理
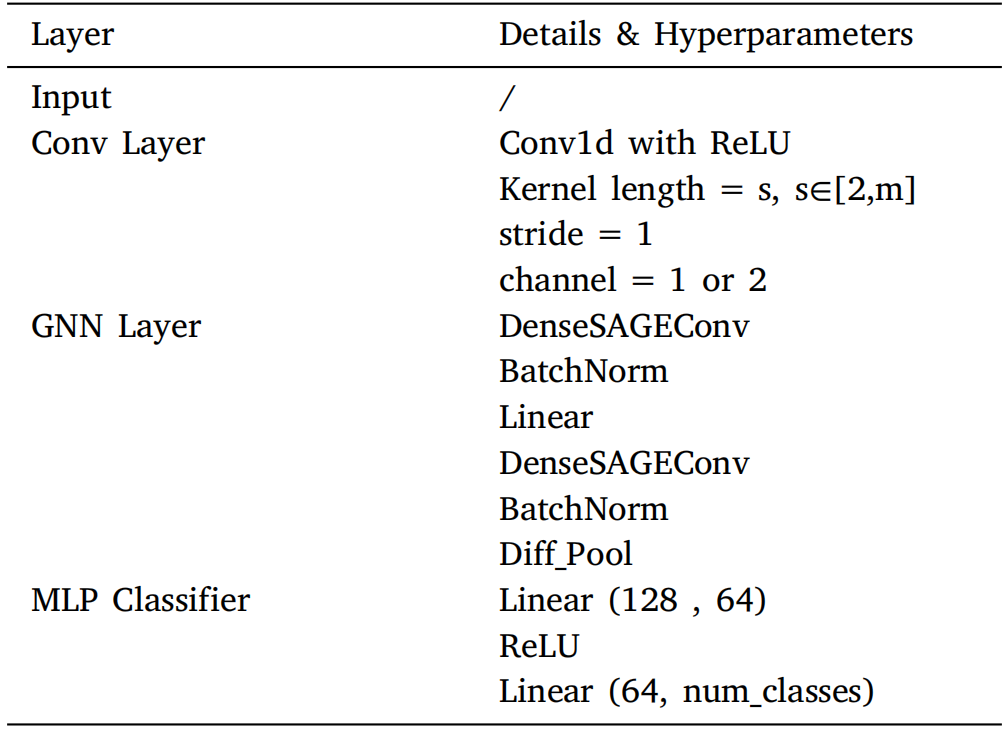
在本研究中,整合了来自五个不同的故障数据集,每种故障类型共采集了 320,000 条数据点。为高效处理该数据,采用了长度为 1280 的滑动时间窗口,并设置聚合步长为 10。该处理流程即每隔 10 行进行一次聚合操作(如最大值、最小值、均值),从而为新的采样点生成一个特征值,最终形成由 128 个节点组成的图结构。为确保样本量均衡,将每类故障信号数据中 70% 分配至训练集,剩余 30% 用于测试集。最终,训练集包含 224,000 个数据点(约合 175 个图),测试集包含96,000 个数据点(约合 75 个图)。具体的模型结构详见表 1。
表1 ACVGN的具体模型架构
5.3 实验分析
案例一:ACVGN 的参数优化。在案例一中,研究了三种聚合技术(最大值、最小值、均值与超参数 m 对ACVGN 模型分类精度的影响。图 7 中的实验结果表明,超参数 m 的引入使ACVGN 算法能够灵活地将时间序列数据映射为图结构,增强了模型的适应性与分类能力。特别地,当 m = 7 时,ACVGN算法在所有五个数据集上均获得了最高的分类准确度,证明该参数设置可通过控制节点邻居数量有效提取相关特征。
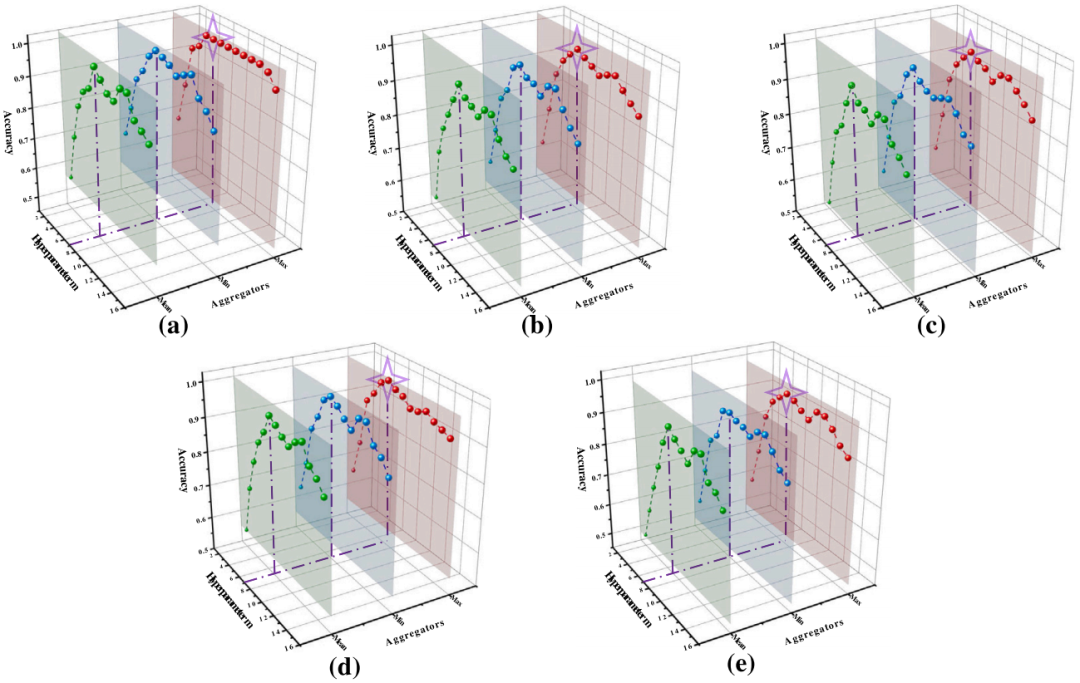
图 7 ACVGN 在五个数据集上分别采用不同超参数 m 和不同聚合方法下的分类准确率变化曲线图。其中:(a)CWRU,(b)BUCEA,(c)XJTU,(d)DIRG,(e)MFPT
研究还发现,在三种聚合操作中,最大值(max)聚合使 ACVGN 模型实现了最佳分类效果。这主要是由于最大值聚合能够提取信号数据中的峰值特征,关键于故障识别,并对一定类型的噪声具备鲁棒性,能在噪声环境中保持峰值检测能力。这进一步凸显了通过合适的聚合方式与超参数 m 调整,ACVGN算法在时间序列数据处理与分类性能方面的潜力。
最后,评估了 ACVGN 算法在不同通道数量下的诊断框架性能,并在四种数据类型下的八个子数据集上均取得了优异的分类结果。模型在多种通道数据类型中展现出较强的通用性与可靠性。如图 8 所示,比较了单通道与多通道数据的实验结果:多通道输入相比单通道输入,分类准确度提升约1%。例如,在BUCEA、XJTU 和 DIRG 数据集中,当使用单通道数据时,ACVGN 的最高准确率分别为 97.68%、96.57%和 99.18%;而使用多通道数据时,准确率进一步提升至 98.82%、97.65%和 100%。这表明多通道数据可提供更多信息,有助于模型进行更有效的特征抽取,提升分类性能。
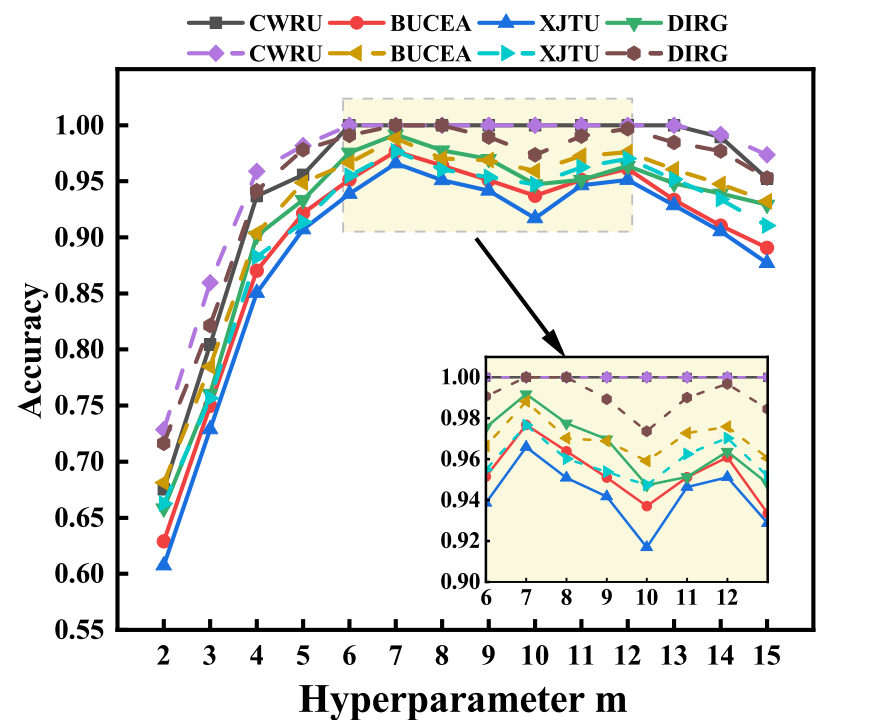
图8 不同通道数据对模型分类准确率的影响(实线表示单通道数据,虚线表示多通道数据)
综上,研究结果突显了 ACVGN 在处理单通道与多通道数据时均具有卓越的分类效果与通用性,显示其在智能诊断与分析中具有重要的应用价值。
案例二:不同图构建方法对模型性能的影响。在基于图神经网络的时间序列数据分析中,将时间序列数据映射为图结构数据是关键步骤。为验证所提出的ACVG算法的有效性,将其与几种常用的图构建方法进行了对比分析。具体而言,选取了两种通用构建方法:KNN 图与半径图,以及两种领域特定方法:可视图(VG)与有限可穿透可视图(LPVG),用于将时间序列数据转换为图结构数据。
随后,利用上述五种图构建方法所生成的图数据,分别应用于七种图分类算法进行实验: GraphSage、图注意力网络(Graph Attention Network, GAT)、GCN、简化图卷积网络(Simplified Graph Convolutional Network, SGCN)、切比雪夫图卷积网络(Chebyshev Graph Convolutional Network, ChebyNet)、图同构网络(Graph Isomorphism Network, GIN),以及高阶图卷积网络(Higher-Order Graph Convolutional Network, HO-GCN)。通过对比不同图构建方法在相同分类算法下的分类准确率,验证了本文提出的ACVG算法的优越性。实验结果如图 9 所示,ACVG算法在多种图分类算法下均展现出更高的分类准确率,表明其在捕捉时间序列数据间关系方面具有更强的能力,从而显著提升了图分类模型的性能。该优势在不同数据集上均得到了验证,进一步突显了ACVG图构建方法的泛化能力。
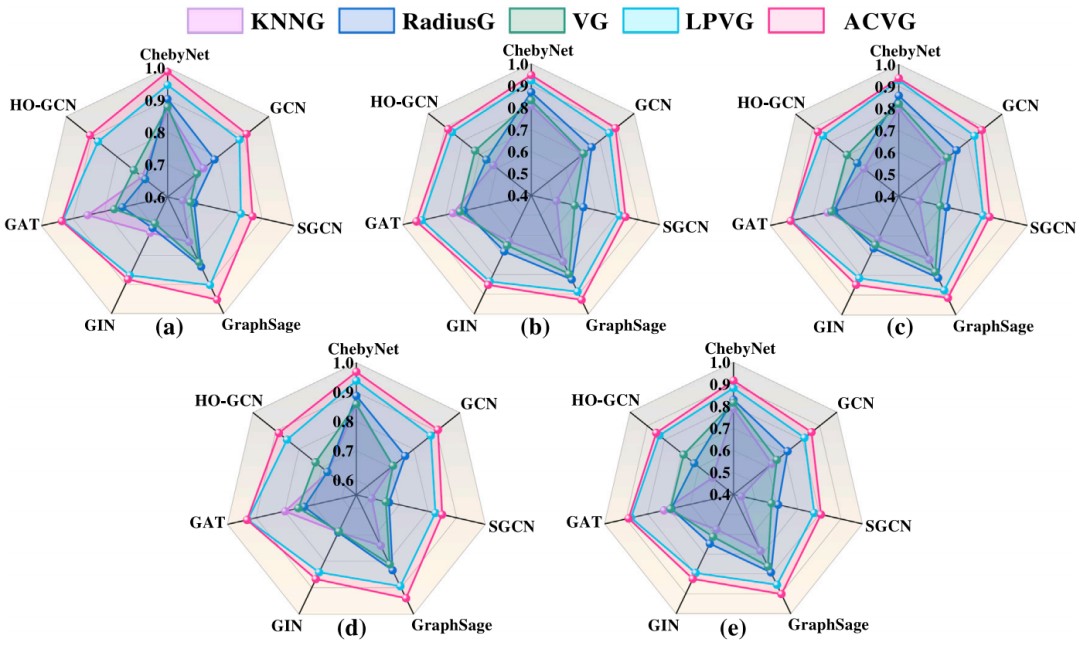
图 9 五种图构建方法在不同数据集上的实验结果表现。其中:(a)CWRU,(b)BUCEA,(c)XJTU,(d)DIRG,(e)MFPT
图 9 展示了在相同图分类算法下采用不同图构建方法时模型性能的显著差异。例如,当采用KNNG与LPVG所映射的图数据作为GAT的输入时,其分类准确率相较于使用RadiusG与VG映射数据有明显提升。而ChebyNet在所有五种图构建方法下均获得了最优结果。
表 2 展示了案例二中七种图分类算法与五种图构建方法在 BUCEA_Bearing 数据集上的分类结果,并标注了每种图分类算法下的最优结果。
表2 ACVG与其他图映射方法的比较
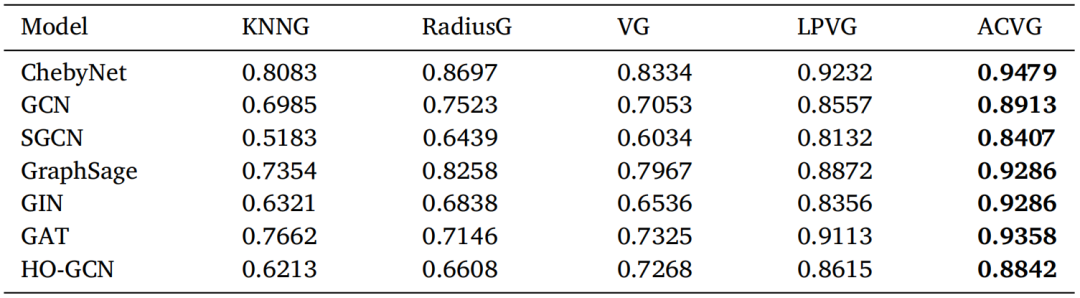
研究结果表明,当采用ACVG算法将时间序列数据映射为图数据作为输入时,七种分类算法的分类准确率均优于其余四种图构建方法。这主要归因于其余四种构建方法的刚性特征,限制了它们对不同数据分布及噪声条件的适应能力,进而影响了其泛化性能。相比之下,ACVG算法具备更强的灵活性,能够更有效地捕捉信号的深层特征,从而显著提升分类精度。这一发现表明,图拓扑结构的先验知识对模型性能具有显著影响,强调了在智能诊断任务中选择恰当拓扑结构的重要性。相比之下,ACVG算法具备更强的灵活性,能够更有效地捕捉信号的深层特征,从而显著提升分类精度。这一发现表明,图拓扑结构的先验知识对模型性能具有显著影响,强调了在智能诊断任务中选择恰当拓扑结构的重要性。
最后,对三种可见域图构建方法VG、LPVG 和 ACVG的时间复杂度进行了分析。对于一个含有 个节点的图, 通过引入超参数 来限定每个节点的邻居数量,其时间复杂度为 。相比之下,VG在图构建过程中需要计算每个节点与 个节点之间的边关系,其时间复杂度为 。而 LPVG 在 VG 的基础上引入了可穿透距离的限制,使其时间复杂度显著高于 VG。值得注意的是,VG 与 LPVG 都需要通过条件语句判断节点之间的边关系,而 ACVG 为矩阵操作,因此可以加载至 GPU 上运行,提升图映射效率并降低映射耗时。在相同数据集输入条件下,分别记录了三种构建方法映射出的十个图,并测量了图数据输入 GCN 算法并完成一个训练周期所需的时间。结果如图 10 所示,ACVG 的图映射时间与单周期迭代时间远短于 VG 与 LPVG,分别仅为 3.17 秒与 1.2 秒。该结果归因于 ACVG 构建方式的灵活性。实验结果表明,ACVG 算法不仅具备较低的时间复杂度,同时在提升图映射效率与分类准确率方面表现优异。因此,在可见域应用中选择合适的图构建方法至关重要。
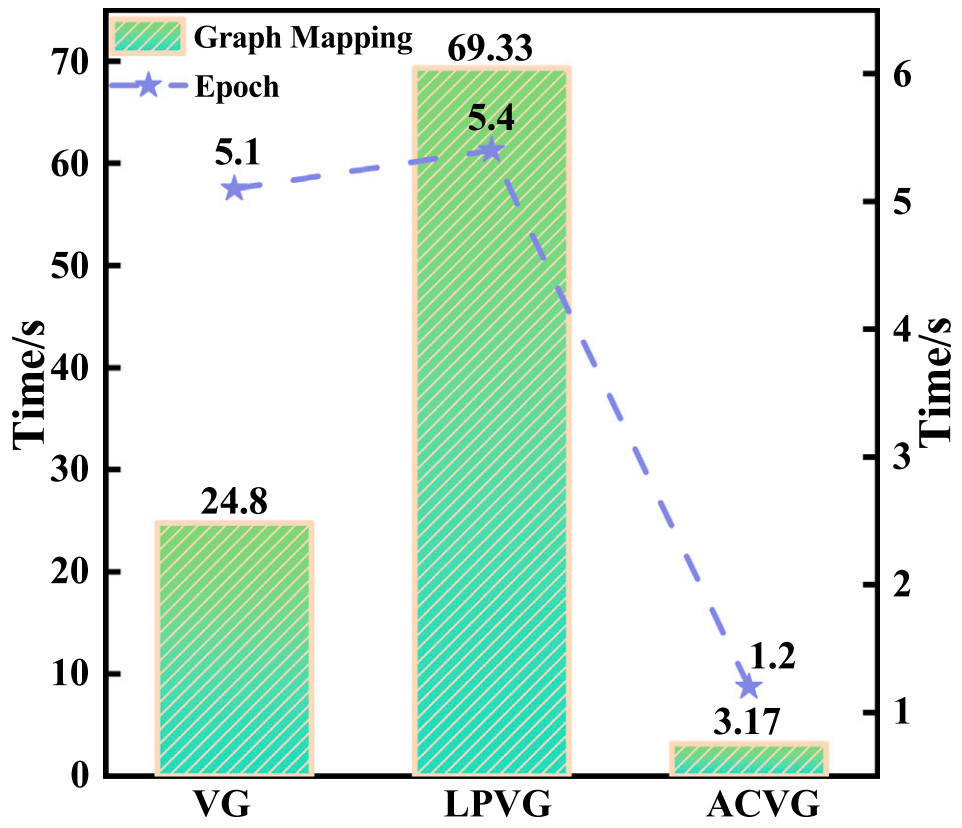
图10 三种图映射方法的图构建时间与单周期迭代时间对比图
案例三:ACVGN 的分类性能评估。在案例三中,通过与三类典型基线模型对比,验证了ACVGN在智能诊断领域的性能表现。首先,采用传统的神经网络模型 LSTM 对故障数据进行分类。接着,使用具有 18 层神经网络结构的 ResNet 模型执行故障分类。最后,将案例二中提到的七种图分类算法(包括 GraphSage、GAT、GCN、SGCN、ChebyNet、GIN和 HO‑GCN)作为对比基线模型。各方法在五个数据集上的分类准确率结果详见表 3。
表3 不同方法在五个数据集上的分类性能
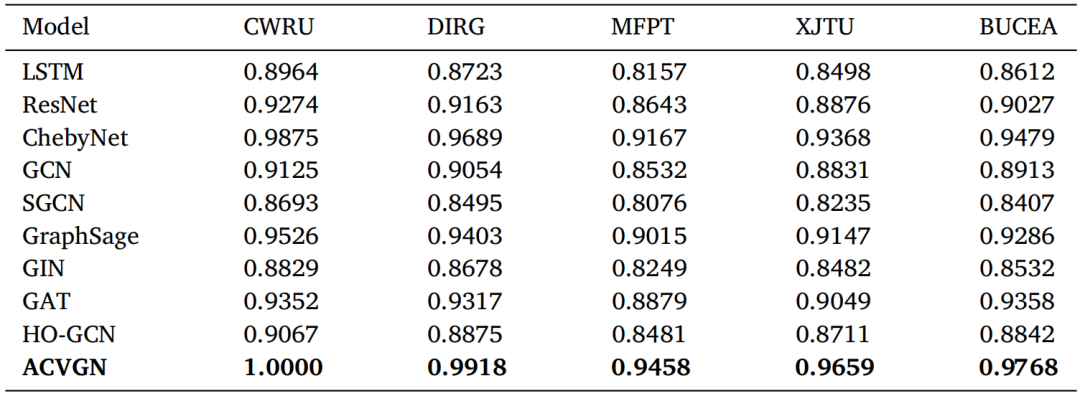
首先,将 ACVGN 与深度学习模型 LSTM 和 ResNet 进行对比。如表 3 所示,ACVGN 在所有五个数据集上都优于 LSTM 和 ResNet 的分类准确率。需要指出的是,LSTM 和 ResNet 分别是时间序列和图像领域的典型深度学习分类模型,在多种任务中表现良好。因此,可以推断:将时间序列数据映射为图结构,有助于捕捉信号间潜在关联特征,并结合图分类模型实现更优分类效果。
其次,将ACVGN与图分类算法 ChebyNet、GCN、SGCN、GraphSage、GIN、GAT、HO‑GCN 进行对比。上述七种图分类算法的嵌入结构列于表 4。
表4 图分类算法的嵌入

对比结果显示,ACVGN在不同数据集上均表现出明显的分类优势,反映出其卓越的泛化能力。这主要归因于 ACVGN模型设计中:其不仅持续提取有助于图分类的节点嵌入,也能融合原始信号的局部与全局信息(通过超参数控制),从而实现优异的训练表现。综上所述,实验结果证实:ACVGN 相比其他基线模型具备显著优势,突显了本文提议方法在智能诊断领域的有效性。
案例四:ACVGN 的可解释性说明。作为一种图分类模型,ACVG能挖掘并可视化从时间序列数据映射而来的图结构,对理解模型的预测与决策过程尤为重要。因此,为增强 ACVGN算法的可解释性,对不同工况下映射出的图进行可视化与对比分析,以示例方式提升模型的可解释能力。
为此,使用生成的加权邻接矩阵对时间序列映射成的图进行可视化。图绘制通过 Gephi 实现,并采用OpenOrd 布局。为突出不同工况图结构间的差异,去除了权重特别微小的边,将边按权重值使用渐变色着色——颜色越深表示边权重越大,即两个节点之间关系越紧密,如图 11 所示。
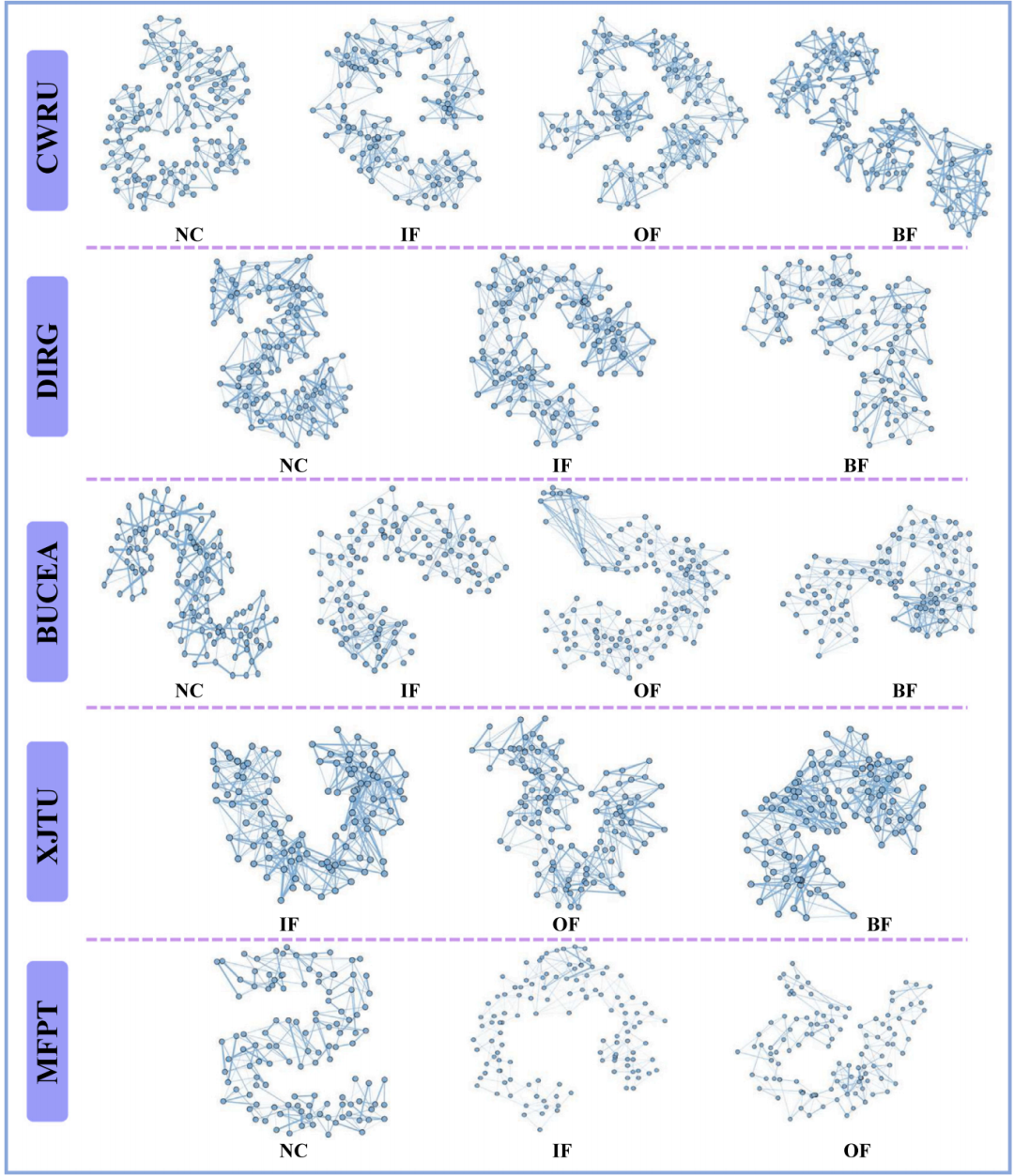
图11 不同数据集中通过 ACVGN 映射得到的图结构可视化结果
通过对节点连接关系分析,可得到以下结果,横向比较:同一数据集中不同工况下的图结构明显不同,有助于故障类型的识别与分类。纵向比较:不同数据集中相同工况对应的图结构表现相似。例如,NC(正常)工况下的图呈现类似英文字母“S”的结构,而IF(内圈故障)工况的图结构则更像大写字母“U”。这是由于不同故障引发的故障频率与振动特征存在差异,映射后的图结构也随之变化。此外,尽管某些工况(如IF 与OF)的图结构相似,但由于ACVGN 的DiffPool 模型不仅输入图结构(邻接矩阵),还结合每个节点的特征向量,因此仍能有效区分它们,实现高精度分类。
6 结论
本文提出了一种先进的的机械设备智能诊断框架——ACVGN。该框架融合了自适应收敛可视图(ACVG)算法与改进的 DiffPool 模型,具备完备的数据处理能力,能够对时间序列数据进行自适应处理,将其映射为最优图结构,并实现局部与全局信息的融合,从而显著提升分类准确率。
所提出的 ACVG 算法能够高效地将时间序列数据转换为图结构,有效克服了传统可视图算法在构图刚性与效率方面的不足。同时,结合经过优化的 DiffPool 模型进行图分类,与自适应可视图算法协同作用,构建出功能强大的 ACVGN 智能诊断框架。该框架在处理时间序列数据时具有良好的适应性,不仅能够生成最优图结构,还能显著缩短映射时间;同时,通过聚合样本中的局部与全局信息,有效提高了故障分类性能。
实验结果表明,ACVGN 框架在泛化能力与分类精度方面均优于现有主流方法。此外,通过对 ACVGN 所映射图结构的可视化分析,揭示了不同图结构之间的差异性,为图学习的可解释性研究提供了新思路。





