04.显式时间步长
LS-DYNA采用的显式中心差分法是有条件稳定的,只有当时间步小于临界时间步时稳定。显式分析通过控制稳定极限来控制时间步长,稳定极限和单元的长度和波速相关;材料的刚度越大,波速越高,其稳定极限越小;密度越高,其波速越低,稳定极限越大。本文介绍时间步长的计算公式和定义方法。
【1】临界时间步长
临界时间步长是通过系统的最高频率来定义的,定义如下:

其中ωmax为最大自然角频率。
由杆件的的自然频率:
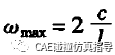
C是波速,L是单元的特征长度。
波速:

临界时间步长:

C是波速,其中L/C是一个弹性应力波传递过该单元的时间;其中 特征长度I和波速c取决于单元类型。
【2】不同单元的波速
①梁单元

②壳单元
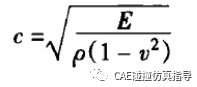
③体单元

【3】LS-DYNA中时间步长
在LS-DYNA中临界时间步尺寸自动计算;它依赖于单元长度和材料特性,在计算时间步时需要检查所有单元,为达到稳定采用一个比例系数(缺省为0.9)来减小时间步。
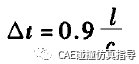
从而对于整个有限元模型来说,控制实际计箅时间步长的是最小尺寸单元,当模型的网格质量不是很好的时候,如有很多的小单元存在,此时计算的时间将成倍增加,为减小计算量,需要人为地控制LS-DYNA时间步长,称之为质量缩放。此时在不改变有限元模型的前提下,加大实际计算时间步长,以壳单元为例,如下图:
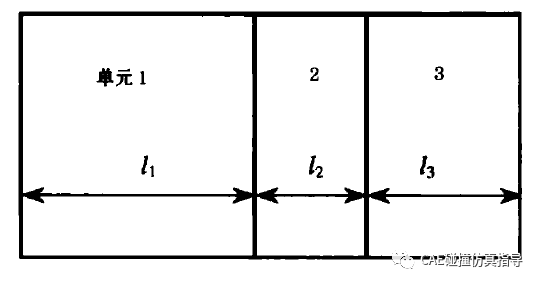
壳单元
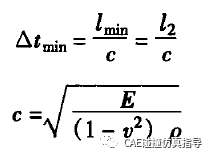
由上面公式可知,可以通过调整该单元的密度来增大它的时间步长〈弹性模量一般不调整,因为接触中需要真实的弹性模量),LS-DYNA由关键字誉CONIROL_ TIMSIEP中参数DT2MS来人为控制时间步长,通过输人期望的实际计算时间步长,程序自动增加对应单元的密度:
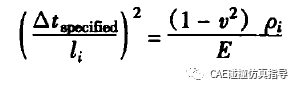
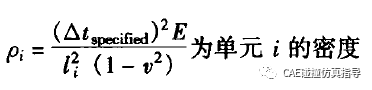
在LS-DYNA中,有两种质量缩放方案:
(1)DT2MS为正的时间步
通过调整单元密度,使得所有单元都具有相同的时间步长,只用于惯性效应不重要时。
(2)DT2MS为负的时间步
质量缩放只用于小于指定时间步长的单元。
使用质量缩放可以显著地降低求解的时间,需要注意的是,某些单元密度的增加必然导致有限元模型整体质量的额外增加,当需要考虑模型的惯性效应时,应该对增加质量的百分比进行控制(同时还需考虑接触的稳定性),即不可任意地设定实际计算时间步长,一般情况下,应控制质量增加百分比在5%之内,在ISDYNA运行窗口中有该参数的显示。
显式分析中,基于时间段开始时刻t,模型的状态通过时间的增量△t发生变化。状态能够发生变化而且要保留对问题的精确描述,一般的时间增量非常短。如果时间增量比最大的时间增量长,此时间增量就是所谓超出了稳定极限。超过稳定极限的可能后果就是数值不稳定,会导致解答不收敛。





