结构力学和结构拓扑优化前沿研究分享
文一:
具有无缝可调各向异性的旋纹超材料的数据驱动拓扑优化
摘要:
我们提出了一个双尺度拓扑优化框架,用于设计具有优化弹性响应的宏观物体,这是通过微观尺度上的空间可变单元结构实现的。在微观尺度上为细胞网络选择的旋节拓扑结构(其灵感来自于旋节分解过程中形成的自然微观结构)允许无缝的空间分级以及可调的弹性各向异性,并且它由与底层高斯随机场相关的一小组设计参数来参数化。宏观边值问题由有限元离散,有限元除了对位移场进行连续插值外,还对微观设计参数进行连续插值。通过假设尺度分离,宏观尺度上的局部本构行为被识别为基于局部设计参数的微观结构的均匀弹性响应。与经典的FE2型方法不同,我们使用深度神经网络,用数据驱动的代理模型取代了昂贵的微尺度均匀化,该模型准确有效地将设计参数映射到有效弹性张量上。该模型基于有限元数值均匀化后的均匀刚度数据进行训练。作为一个额外的好处,机器学习设置允许自动微分,这样就可以准确地计算灵敏度(优化问题所需的),而不需要数值导数——这一策略的前景远远超出了弹性刚度。因此,该框架为基于数据驱动代理模型的多尺度拓扑优化提供了一个新的机会。
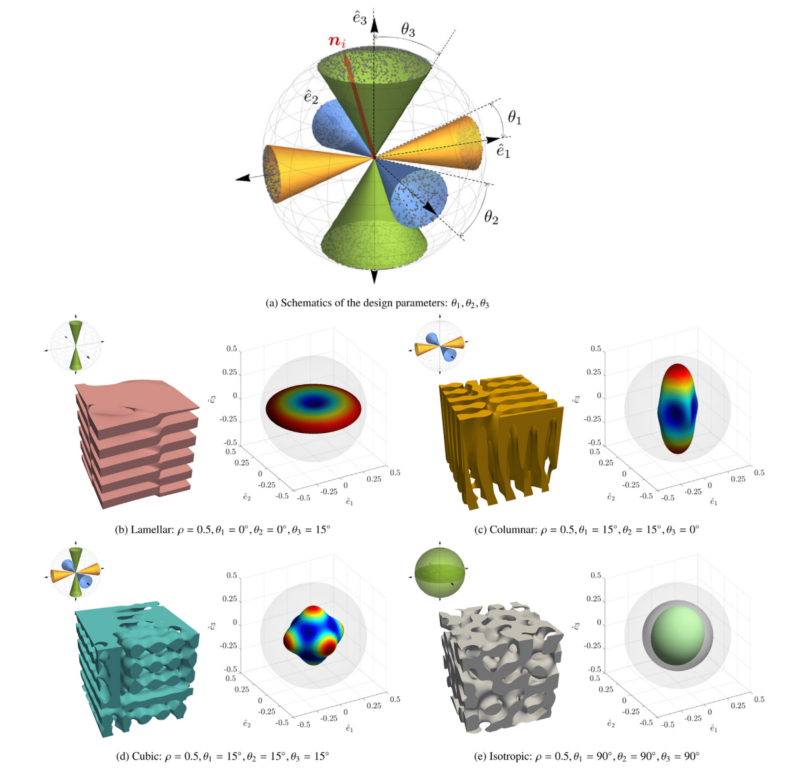
图:旋纹拓扑生成及其代表性实例
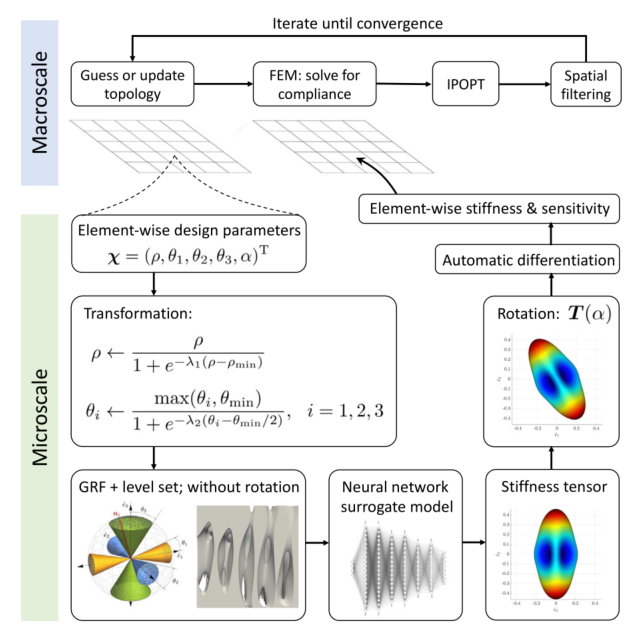
图:超材料结构拓扑优化框架的示意图。
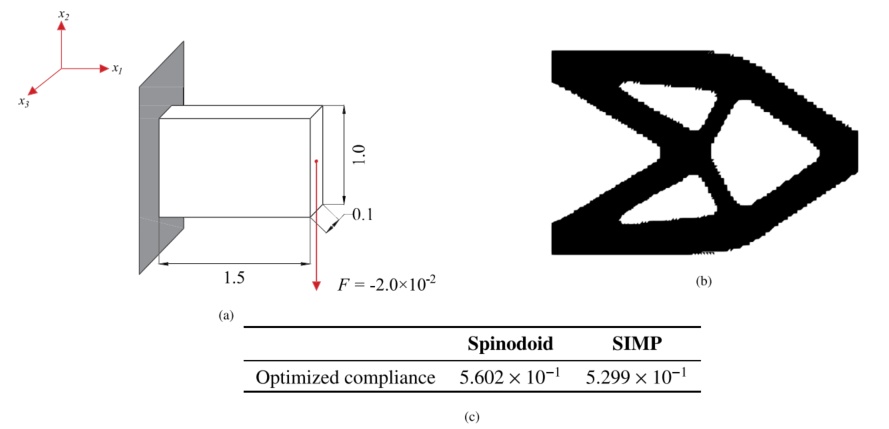
图:基准I:(a)端部加载悬臂梁的示意图,其顺应性有待优化。(b) 使用SIMP方法获得的最优拓扑的前视图。(c) 在微观尺度上(通过所提出的方法)和固体材料(通过SIMP)的旋纹结构的最佳顺应性的比较。
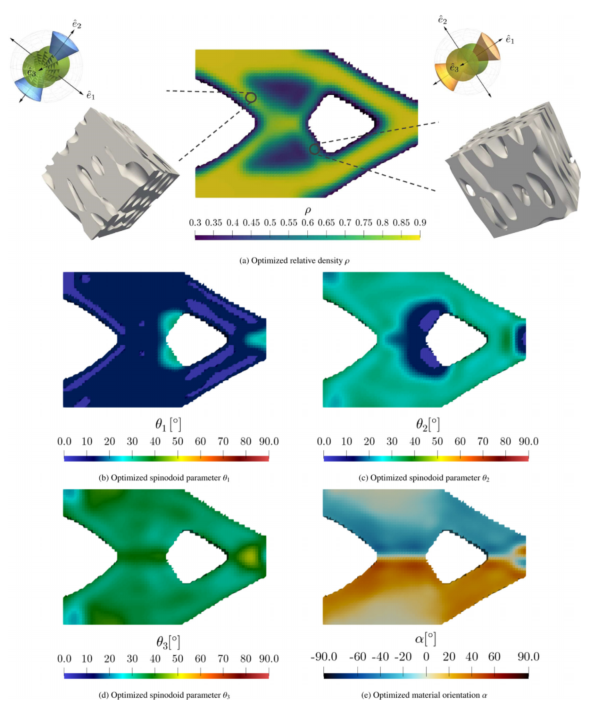
图:基准I:具有棘状微尺度结构的悬臂梁的最佳拓扑结构(材料分布、各向异性和取向)的前视图。空间变化的设计参数在整个机身上进行了说明,(a)中显示了两个不同微尺度拓扑的例子。
文二:
具有最小动态柔度的双层网格填充涂层结构的多尺度拓扑设计
摘要:
本文提出了一种新的多尺度拓扑设计策略,用于填充逐层双材料晶格微结构的涂层结构,其目标是最小化宏观结构在时谐激励频率下的动态柔度。双材料微观结构的优化与宏观结构的拓扑设计同时进行,以充分考虑两个尺度之间结构演化的相互作用。在宏观尺度上,采用基于速度场的水平集方法对宏观结构的材料分布进行优化,该方法继承了隐式几何表示,可以获得光滑的结构边界。由于符号距离特性,在迭代过程中能够很好地保持外涂层的厚度。对于微观尺度,选择密度法对晶格微观结构进行拓扑优化。涂层结构的网格填充物被设计为分层的,将其均匀(或接近均匀)划分为不同的层,每层都由周期性和均匀的双材料微观结构组成,这可以扩大设计空间,产生各种微观结构图案,以更好地抵抗振动响应。对不同尺度的设计变量进行了动力柔度的灵敏度分析,并通过几个算例研究了划分层数、激励频率、涂层厚度、阻尼系数、单元网格、静态约束和网格填充的划分方向对优化的宏观和微观结构的影响。此外,还构建了计算机辅助设计(CAD)模型的贴体网格,有限元分析结果进一步验证了该方法的有效性。
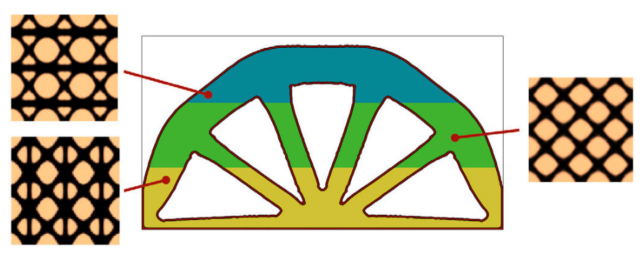
图:填充层状双材料晶格微结构的涂层结构示意图。
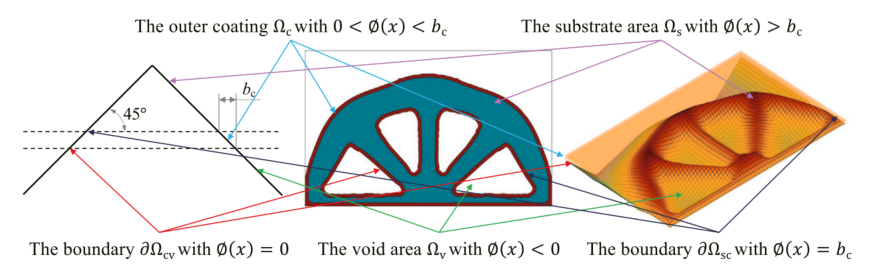
图:具有均匀厚度外层涂层的涂层结构图解。
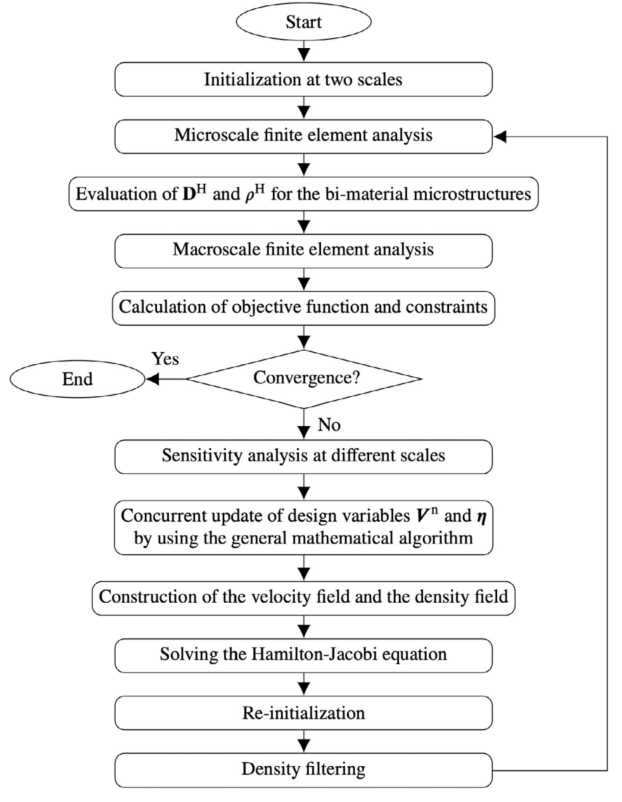
图:优化流程图。
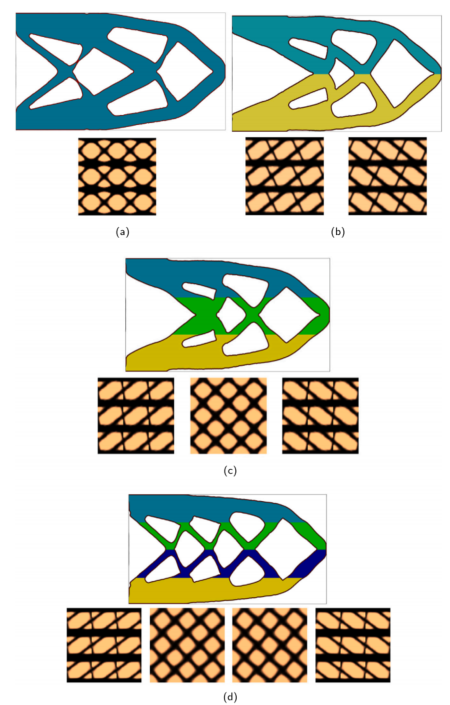

图:优化流程图。
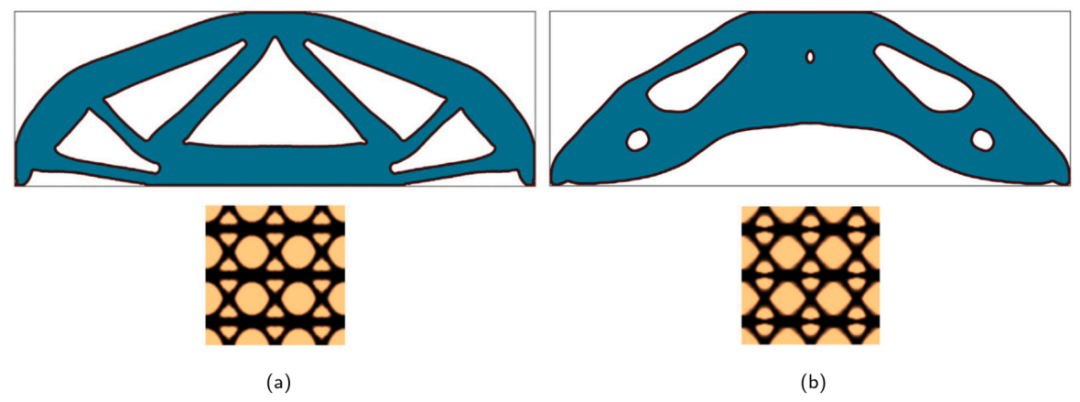
图:不同激发频率 MBB 束的宏观和微观优化结果: (a)5Hz; (b)45Hz。
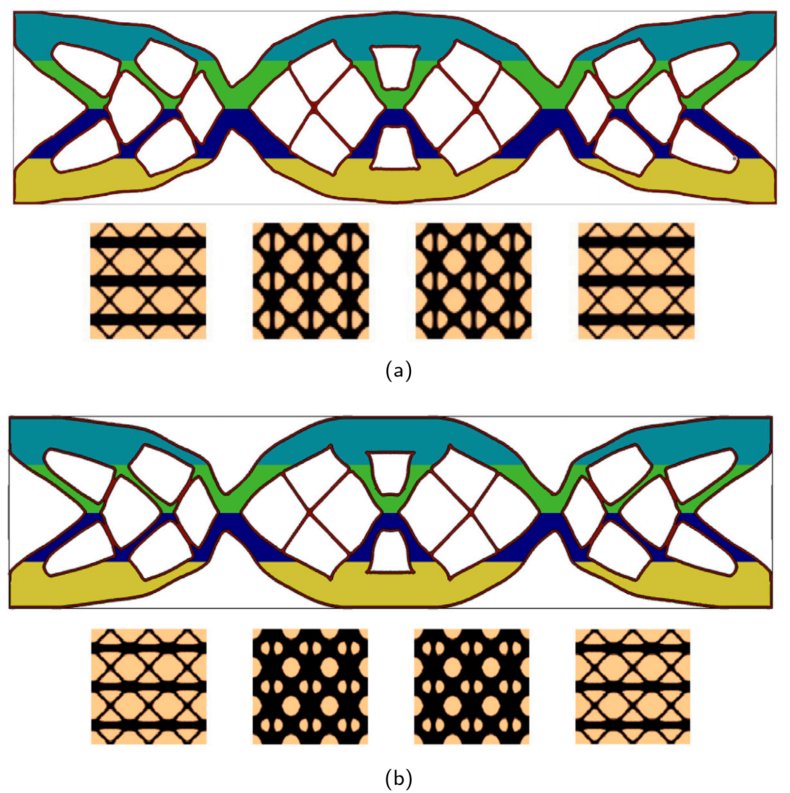
图:填充四层晶格微观结构的夹端梁的宏观和微观优化结果,其中(a)宏观单元网格:400×100,微观单元网格:40×40;(b) 宏观单元网格:800×200,微观单元网格:50×50。
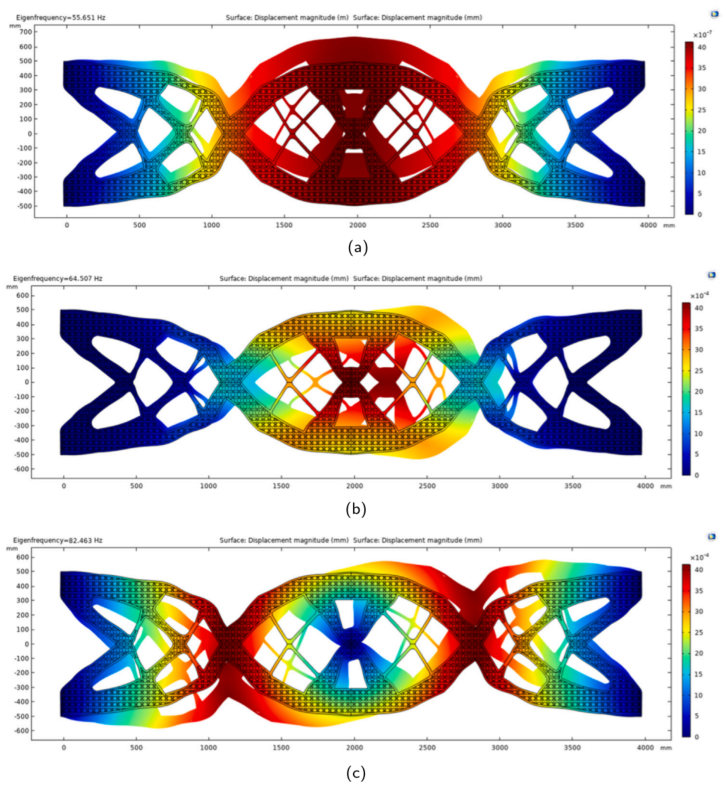
图:优化夹持端梁的本征模形状: (a)第一、(b)第二、(c)第三本征模态。
文三:
表面纤维增强增材制造零件的全尺寸拓扑优化方法
摘要:
考虑到纤维布局和基材分布的灵活性,增材制造为纤维增强复合材料结构提供了新的设计空间。因此,本研究开发了一种专门用于表面纤维增强设计的拓扑优化方法。靶向部分由增强边界轮廓的纤维成分和填充结构内部的各向同性基底材料组成。重点介绍了纤维含量全尺寸建模的思想和解决双模量加固效应的方法。具体而言,在SIMP框架下,通过双层密度平滑和投影的边界层提取来识别纤维含量(包括纤维材料和包裹基质材料),并通过从边界层提取分析骨架来识别增强纤维材料。以这种方式,对恒定厚度的纤维含量进行建模,更重要的是,将其严格纳入拓扑优化问题的公式中。边界层厚度和纤维增强层厚度都可以通过修改投影阈值参数来明确控制。在当前的研究中考虑了顺应性最小化问题。导出目标函数和约束函数的灵敏度,以指导设计更新。提供了几个数值和实验例子来证明所提出方法的有效性和有效性,特别是揭示了引入边界层纤维对导出拓扑结构的影响。

图:边界纤维增强3D 打印工艺规划示意图。
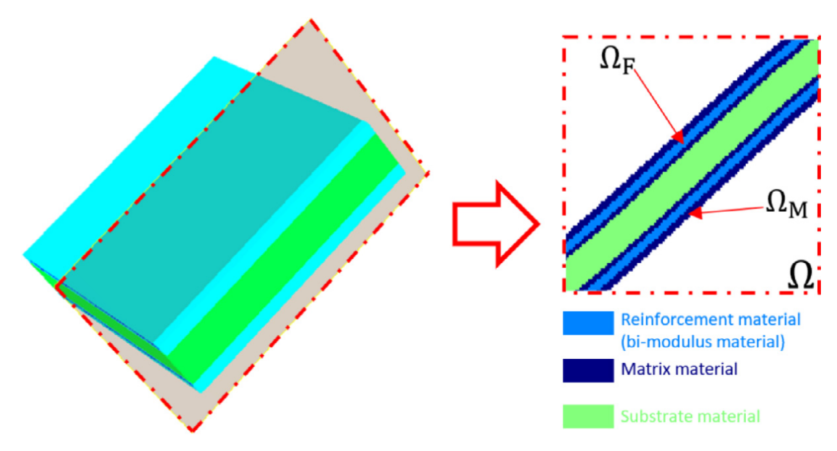
图:全尺寸光纤建模的示意图。
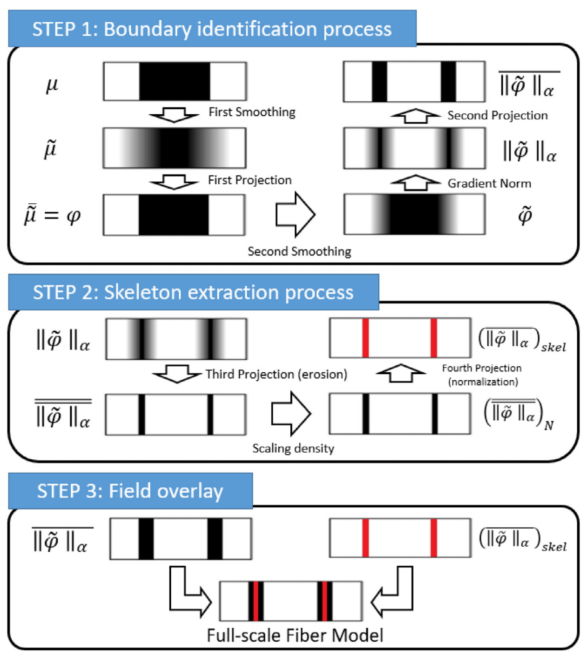
图:边界识别、骨架提取和场叠加程序说明。
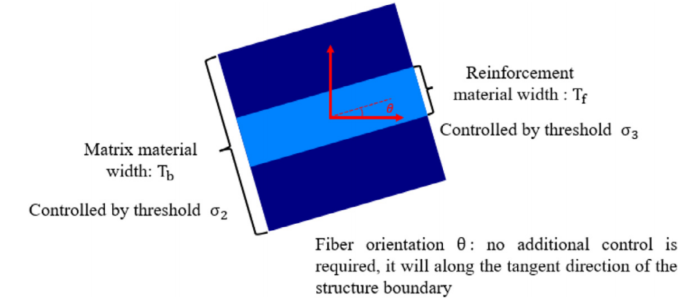

图:全尺寸光纤图案的示意图。
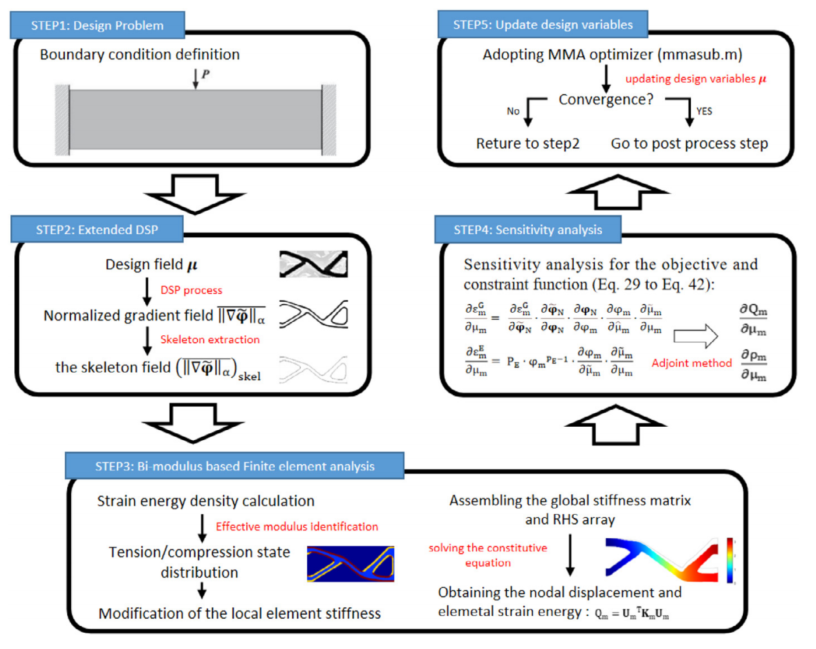
图:所提出方法的流程图。
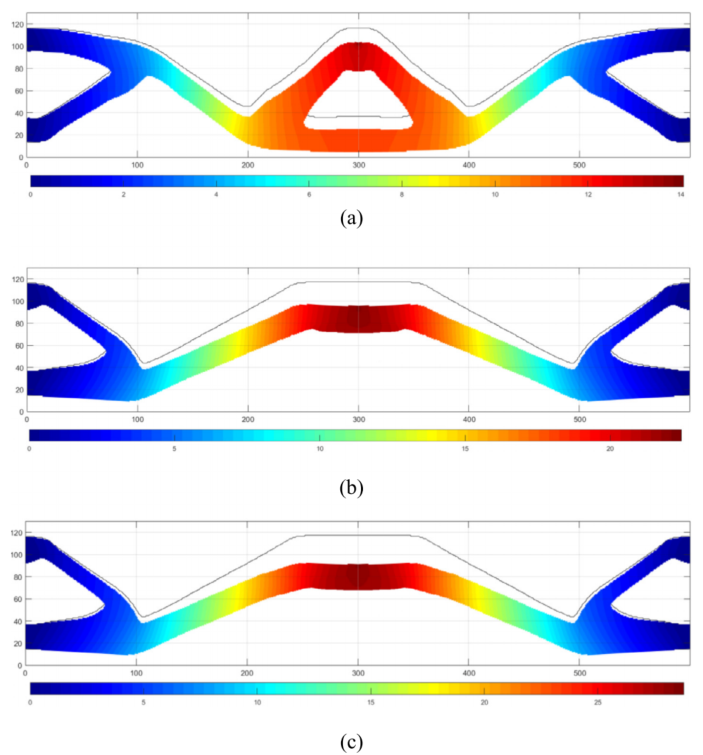
图:(a)双模量边界纤维增强优化结构设计的节点位移分布;对于(b)传统涂层结构的优化设计;以及(c)人工制造的混合设计。
文四:
基于对偶序列二次规划的双圆盘系统刚度和强度拓扑优化
摘要:
针对同时考虑刚度和强度的双盘系统轻量化设计问题,提出了一种基于独立连续映射(ICM)方法的两阶段拓扑优化框架。首先,建立了拓扑优化公式,以保证优化设计满足关键节点的位移和应力约束。其次,引入信息函数来实现元素和组件之间材料特性的转换。选择复合指数滤波器函数来建立元素属性与相应拓扑设计变量之间的关系。第三,通过灵敏度分析和泰勒展开得到近似显式二次规划模型。在求解过程中,利用对偶理论建立了设计变量较少的近似对偶模型。最后,提出并讨论了一系列双盘系统拓扑优化设计问题,以说明该方法的稳健性和可行性。该研究发现了一些新的扭转双盘设计,也为多组分系统的轻量化拓扑优化提供了一些理论参考。
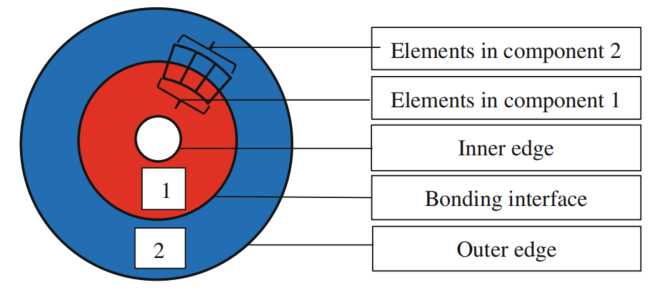
图:双盘系统的设计领域。
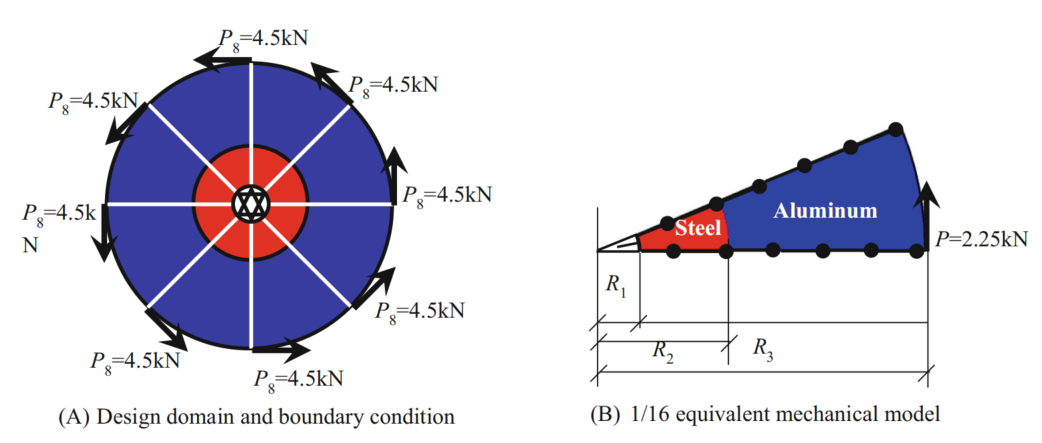
图:具有8个加载点的双盘系统初始设计的力学模型。
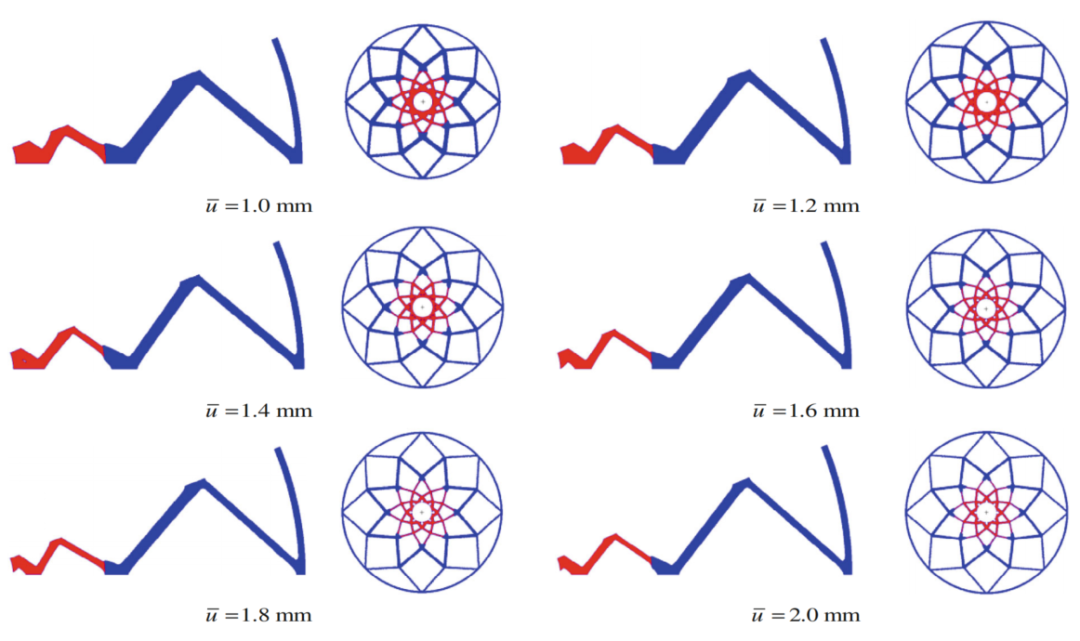
图:具有不同位移约束值的优化结构。
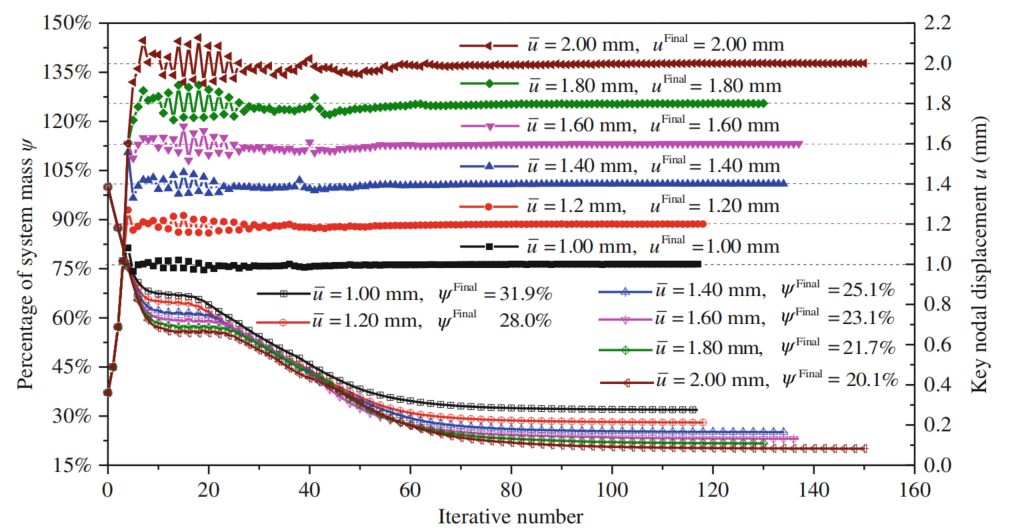
图:不同位移约束值下结构性能的迭代过程。
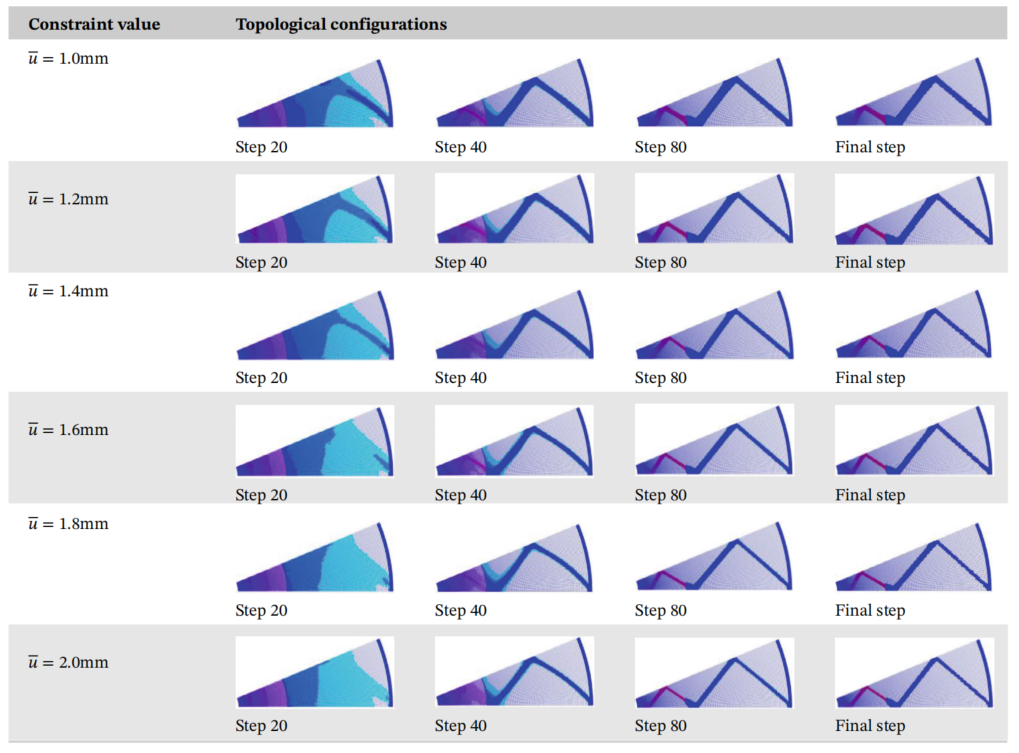
图:不同位移约束下优化过程的拓扑结构。
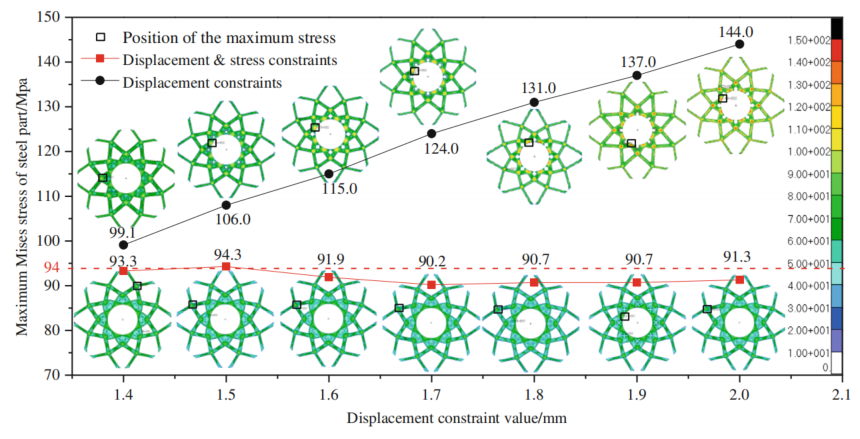
图:不同约束类型钢的最大 Mises 应力。
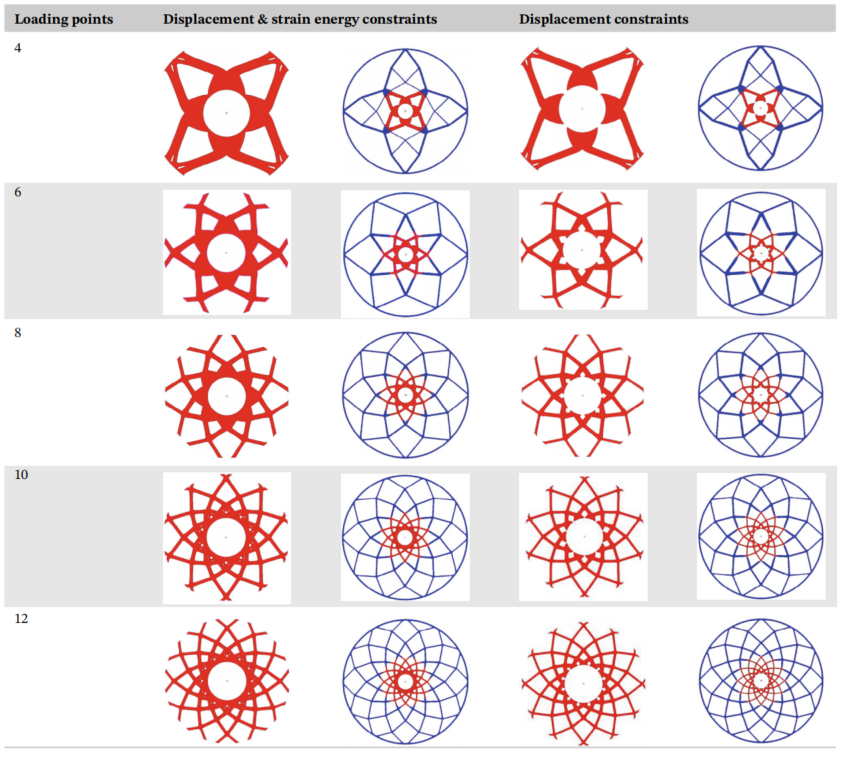
图:基于不同约束类型的光滑优化设计。
文五:
冷却系统设计中热-流-结构问题的三维拓扑优化
摘要:
本文研究了热流体结构问题的拓扑优化方法,以设计具有承载能力的三维散热器。优化公式化为由Navier-Stokes(N-S)方程以及能量平衡和线性弹性方程控制的平均温度最小化问题。为了防止不切实际的低承载设计,流体装置的功率耗散和承载表面上的法向位移被视为约束。多物理拓扑优化问题的并行求解器是内置的开放域操作和操纵(OpenFOAM)软件。灵敏度分析采用连续伴随法,最大限度地利用内置求解器。利用所开发的工具,对三维热流体拓扑优化进行了研究。研究发现,适用于流体设计的达西数可能会给热流体优化带来严重问题。还研究了三维热流体结构问题的结构特征。“2D挤压设计”有助于提高结构刚度,在高温区域具有较大纵横比的通道可以提高冷却性能。
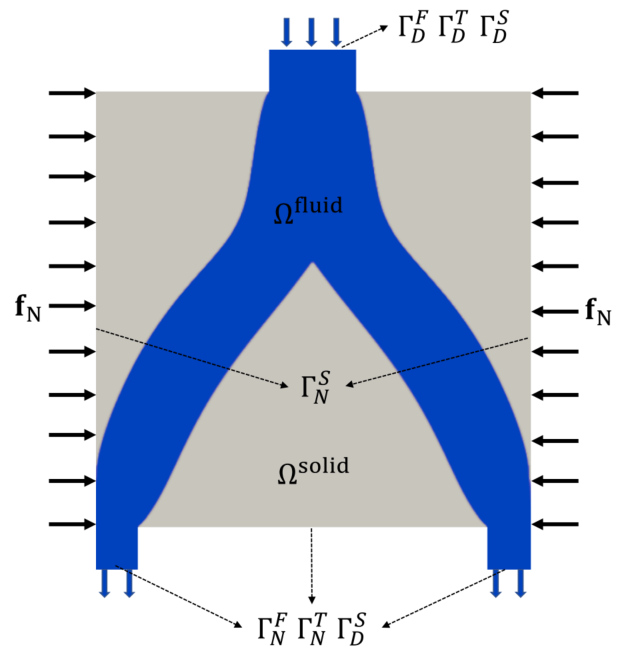
图:分析域的示意图,包括边界的定义。
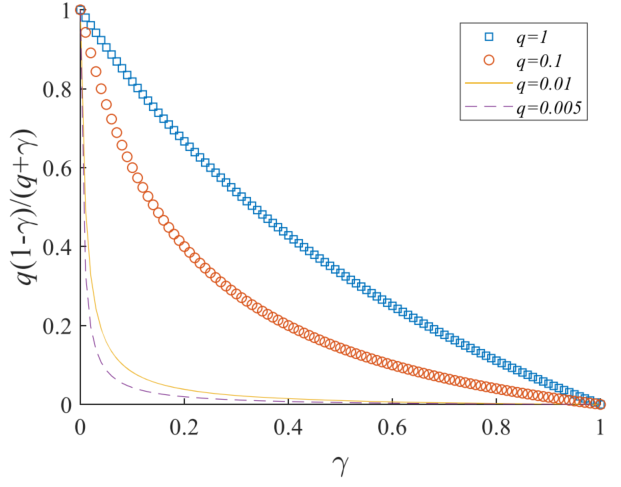
图:曲率参数q的不同值的插值函数。
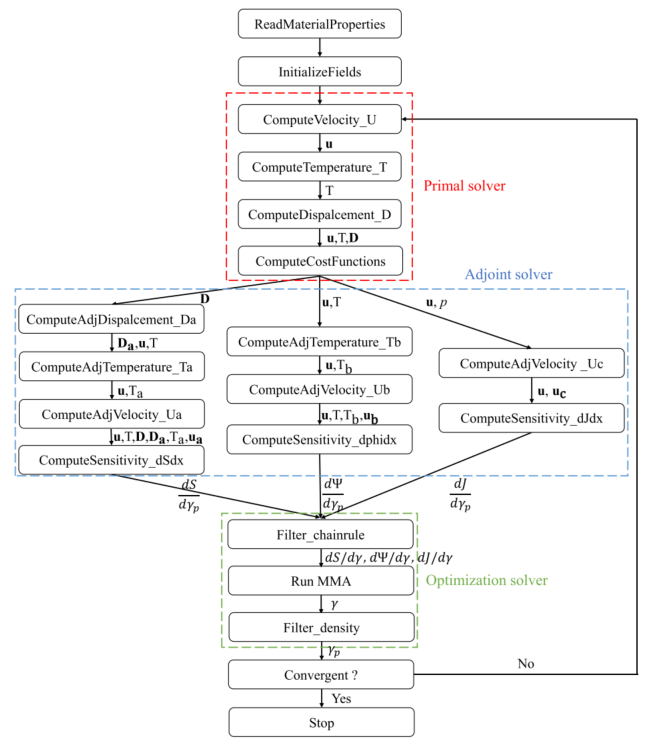
图:优化过程的流程图。
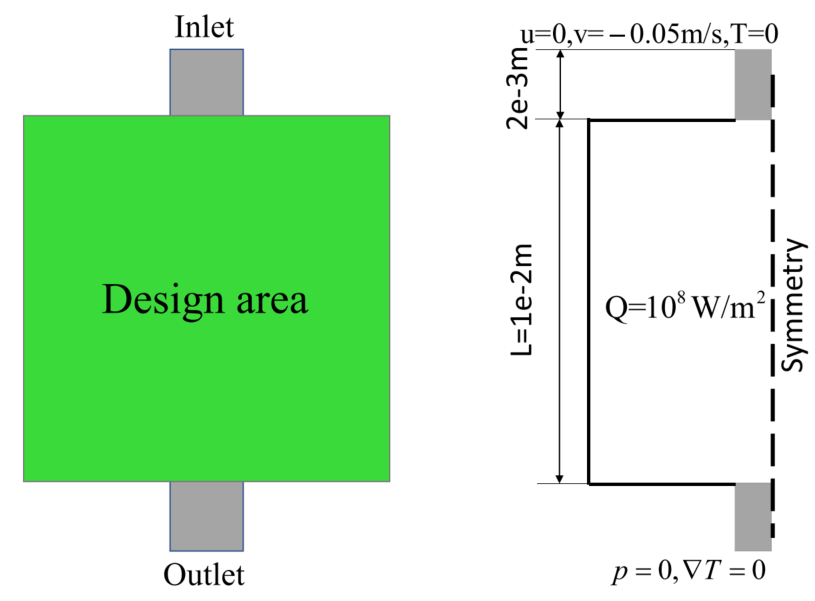
图:二维模型的几何和边界条件。

图:三维直线冷却通道示意图(红色和绿色 区域分别表示流体和固体)。
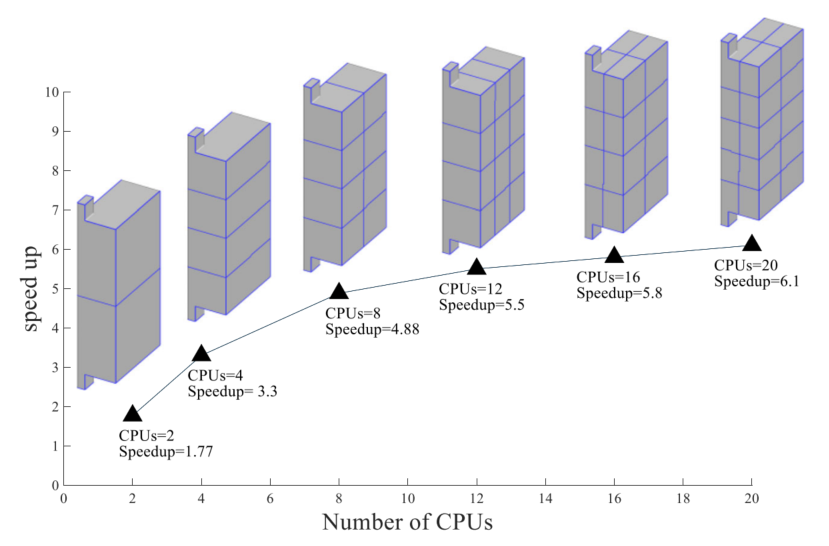

图:提高并行优化求解器的速度。
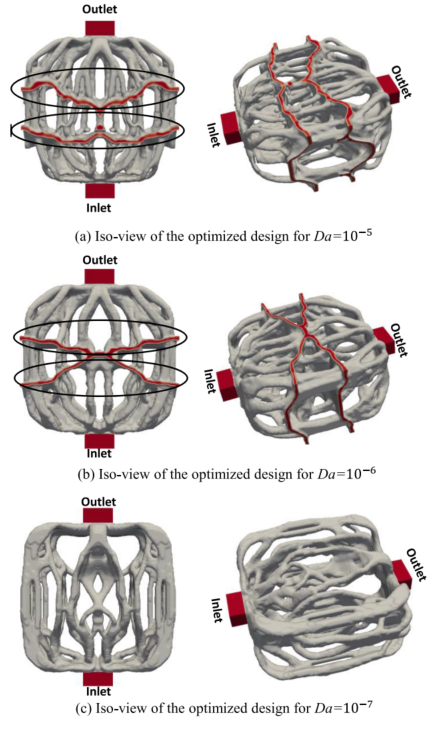
图:三维热流问题的最优解。
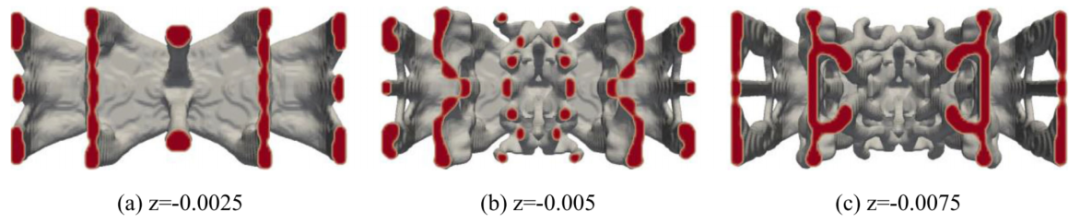
图:情形 B 最优结果的一些截面。





