黏弹性：广义Maxwell模型本构理论推导

本文摘要：（由ai生成）

本文深入探讨了二阶及以上的广义Maxwell黏弹性模型理论及其实现方法。文章介绍了高阶微分形式的广义Maxwell本构，包括一维到三维模型的推广，并提出了简化模型控制方程的方法。文章还将理论应用于UMAT列式，提供了一种更通用、易扩展的黏弹性格式。该科研笔记旨在帮助有需要的读者，同时作者欢迎读者反馈并承诺提供UMAT本构代码。

0. 上回书说到

2024年1月30日，小喵发了一篇文章：

黏弹性：从一维模型到三维UMAT本构实现

里面介绍了基础的黏弹性模型，包括Kelvin和Maxwell形式的标准线性模型（Zener模型），如何从一维推导向三维，以及如何将微分形式的本构关系与Prony级数形式的公式联系起来。

这篇文章在此基础上更进一步，讨论一下二阶及以上的广义Maxwell模型的理论，以及如何实现。

 

备注：这篇文章是小喵出于自身科研需要而总结。我自己也是学习者，一边推导一边写成了这篇推送。限于能力和水平，无法100%保证全部推导都是正确的，只能说我已尽我所能保证推导和讲解过程的可读性和准确性。

这篇文章，本想把UMAT代码都写完后再一起发出来。但鉴于后续时间安排，恐怕就又要延后一星期甚至更久。写到这里Markdown源文件已经有超过18,000个字符，考虑到篇幅因素，还是决定把公式推导部分提前单独发出来。

正文目录：

• 0. 上回书说到

• 1. 高阶微分形式的广义Maxwell本构

• 2. 引入局部应变的简化形式

• 3. 广义Maxwell黏弹性UMAT列式

• 4. 结尾和预告

观前提醒，如果读到某个公式卡壳，千万不要死磕。第1节的公式形式复杂，到第2节会变简单。

1. 高阶微分形式的广义Maxwell本构

让我们回顾一下，从一根Maxwell黏弹性元件开始。

 

弹簧和阻尼器串联，两个元件应力相等，总应变等于二者叠加。因此Maxwell元件的控制方程可以用应变率的形式写为：

那么，对于一根刚度为     的弹簧和一根     的Maxwell元件并联组成的，Maxwell形式标准线性模型（这里把弹簧刚度的下标修改成0，是为了和后面广义Maxwell模型一致），它的弹簧和Maxwell两个元件并联，应变相等，应力为二者叠加。

 

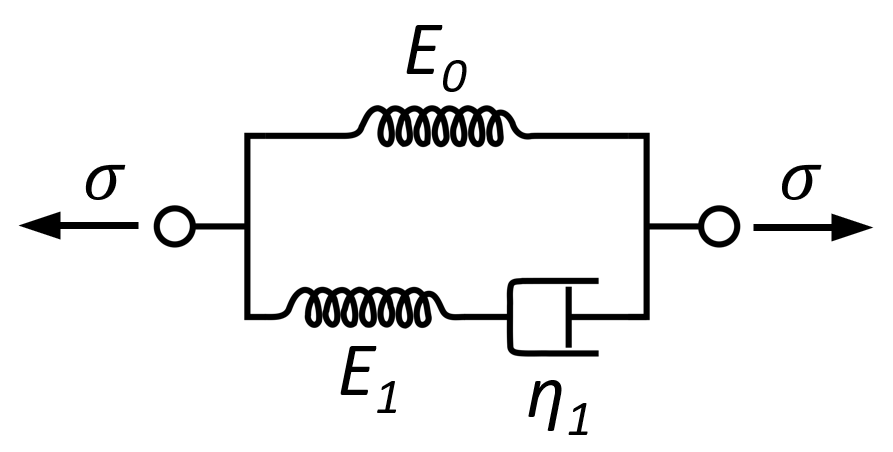
对于弹簧元件，有：

对于Maxwell元件，和前面公式    一样：

这里我们使用一个比较通用的推导方式，方便向高阶推广：从应力的零阶导数项开始，试着让方程中不要出现    这种局部元件应力，只有整体应力    。

为了实现这个目的，我们首先写出：

将公式    做简单的变形，结合公式    ，可以写出：

很显然，公式    还不够干净。它的右侧还多出来一个     项。

为了把它平衡掉，我们回头来看公式     。把公式     左右两边同时对时间求导，形式还是不变的：(求导符号我也懒得改正体了，太麻烦了，毁灭吧……摆烂.jpg)

这样就有了     。我们用它来平衡掉公式     中应力对时间的一阶导数项，就得到：

引入弛豫时间     ，简单整理一下，就大功告成：

式     就是一阶广义Maxwell黏弹性模型的控制微分方程，描述应力和应变（以及它们的时间导数）之间的关系。很简单，很好理解，对不对？甚至对于刚才我们推导的一阶广义Maxwell模型来说，仅靠观察也差不多能得到这个结果，随便怎么推都能推出公式    来。

——————

那现在让我们考虑二阶广义Maxwell模型。模型里的参数分别为     。

对于弹簧元件，显然有（这次我们直接准备到二阶导数）：

对于两个Maxwell元件，和公式    一样。但这次我们也给它多准备一阶的时间导数：

还是和刚才一样，首先写出     ：

果然，这次的公式     里面想要再直接用弹簧元件的一阶导数是不能摆平了。因为这次两个局部应力导数前面的系数不同。

那么为了伺候这两位爷，我们构建出下面的形式：

在    里面，把    那两项刨除掉，剩下的几个导数项，把    里面对时间求过一阶导的公式拿出来，简单变变形：

综上,我们把公式     和    放在一起，合并同类项：（这公式已经有点长了）

诶，现在我们可以发现，在公式    中不平衡的    两个时间导数项，在公式    里面系数变得一致了。这样，只需要在公式    中补充上    的项，即可完全消去局部应力，得到整体应力-应变之间的微分关系。

所以最终，二阶Maxwell黏弹性模型的控制方程，我们这里就可以参考之前黏弹性的推导，引入弛豫时间    ：

最终形成公式    。类比一下，和前面的公式    形式很像，对不对。

到这一步，我们可以大致用文字总结一下。

对于包含1个弹簧和N个Maxwell元件的广义Maxwell黏弹性模型，为了推导出其总应力-总应变之间的关系，需要列出每个局部元件的控制方程，并将每一行方程对时间求导。然后从应力对时间的零阶导数开始，逐层将局部元件的应力加总。这一过程总会残留下应力对时间的更高阶导数项。重复此过程，一直到应力对时间的第N阶导数项才可以被完全配平。

（好像用文字怎么描述都说不太清楚。不过如果你认真跟着前面的推导读下来，相信你一定可以理解这段话。）

推广到N阶，对于包含共计1个弹簧和N个Maxwell元件的广义Maxwell黏弹性模型，其控制方程的一般形式为：

——————————

前方高能。这个形式来自维 基 百 科，可难写了……

——————————

稍微展开一点，另外一种通用形式：

我已经懒得再仔细解释上面那两坨公式了。总之，按照前面的推导逻辑，N阶广义Maxwell模型的控制方程里确实需要包含应力和应变对时间的最高N阶导数。

推导结束，可喜可贺……是吗？

如果有限元软件里的广义Maxwell黏弹性模型要拿上面的控制方程去写代码，那这代码的繁琐程度恐怕就不是一般人类能看懂的了。

2. 引入局部应变的简化形式

还有没有更简洁一点的形式呢？ 就，类似之前我们看到过的Prony级数，对于广义Maxwell模型的松弛模量，多一阶只需要加一项（而不是提升一阶导数）：

——那肯定是可以的。

仔细想一想前面的推导，我们为什么要这么麻烦地去不断提高应力和应变对时间的求导阶次？

答案是为了得到总应力和总应变之间的关系，在方程里抹掉所有局部元件的信息。

那么，如果我们在方程里保留每一个局部的信息，会怎么样呢？

实际上，这就相当于在控制方程里引入更多额外的变量，提高方程组的维度，从而降低方程组的阶数。

来，一起来见证魔法。

仍然以最简单的一阶广义Maxwell模型为例。

 

这一次，我们在列出     的时候，不再追求把两部分应力合并在一起，就这么分开放着。本构关系是应力与应变之间的关系。那么既然要把     和     分开，也就要多定义一个独立的应变。很显然——在这个模型里，我们可以把Maxwell元件中阻尼器的应变单独写出来。

将阻尼参数为     的阻尼器应变定义为

那么   那根弹簧的应变就应该是   

这样，弹簧部分本构仍然是

Maxwell部分的本构：

这次在式    中，我们要用     和     来表示     ，而不要出现高阶导数     。这也不难，只需要把式    对时间的导数降低一阶：

就可以写出一阶广义Maxwell模型的控制方程了：

很显然，模型中的     实际对应Maxwell元件的应力卸载到零时，黏弹性模型的长期模量；而     对应的则是黏弹性模型的瞬时模量。

（投共一念起，刹那天地宽。）引入黏壶应变     后，我们发现式     这样的黏弹性控制方程形式一下子简洁了许多。同理二阶广义Maxwell黏弹性模型的控制方程就可以写为：

直接就可以把N阶控制方程的通用形式都写出来了。

当然，增加了N个变量，还需要相应地补充N条方程，说清楚     和     之间的关系。这并不难。对式     做一个变形：

式     构成了完整的N阶广义Maxwell黏弹性模型的控制方程。

绕了一大圈，原来这么简单就解决了啊。那你早说呀，我前面还吭哧吭哧推那些公式干嘛呢。

3. 广义Maxwell黏弹性UMAT列式

现在，有了前面的公式     ，再来审视一下黏弹性本构模型的UMAT。让我们把它修改成更通用、更方便扩展的广义Maxwell黏弹性格式。

从式     出发，这个本构直接可以推广到三维。三维的广义Maxwell模型本构关系可以用张量记法写为：

其中，上标显然不表示乘方，主要是下标被张量标记占了只能写成上标。     是和第n个Maxwell元件关联的阻尼器内应变，    是对应的弹簧刚度。第一个     是瞬时模量，    和前面的    一样都是四阶弹性张量，具有相同的形式。每一个     都服从以下关于时间的微分方程：

根据公式     ，其实就可以直接写出相应的具体有限元列式。为了使方程形式简洁，使用     两个变量作为弹性常数。将初始（瞬时）Lamé常数记为     ，一阶广义Maxwell元件对应的刚度为     ，相应的弛豫时间为     。则式     可以用张量的形式展开为：

 

这里的符号记法与前文略有出入：前面描述广义Maxwell模型的时候，我们将并联的单个弹簧单元的刚度写成     ，下标为0以和其他Maxwell元件形成区分。但实际上我们知道那根弹簧的刚度    其实是整个模型的长期模量。

在后面的推导中，我们为了和Abaqus文档里的黏弹性公式保持一致，将初始的瞬时模量下标写为0，而将长期模量的下标写为     。例如，瞬时Lamé常数为    ，对应的长期模量数值为     （读者如果要参考本公 众  号文章来组织自己论文中的公式，请自行斟酌标记的前后逻辑一致性）

写成矩阵形式（哎呀这段LaTeX可难写了）：

 

要注意，在Abaqus文档页

Abaqus > Introduction & Spatial Modeling > Conventions > Convention used for stress and strain components

里面，介绍了Abaqus以向量形式存储张量分量的顺序。上面使用的顺序是Abaqus/Standard的存储顺序。Abaqus/Explicit使用了不同的顺序：    这样。

另外，同一页文档还写明，Abaqus始终使用工程剪应变，    ：

所以后面的     剪切分量，我这里也自动乘了2.

同样使用中心差分列式（此处下标表示该变量所处的时刻），

式     可以写为：

化简后得：

式     的形式就可以简单地扩展到2阶乃至更高阶的Maxwell黏弹性模型：

 

这里常数的n写成了下标，局部应变    的n则写成上标，实在是为了尽可能在符号表达上前后逻辑一致，没有正经张量分析里面上下指标平衡求和的说法。但好像……n在这里确实变成了哑指标，也确实有一个最大N阶的求和符号，但那个纯属意外。只有    的下标k是需要按照张量规则（爱因斯坦求和约定）来求和的。

在UMAT实现中，还是要根据上一步的应力     、应变     和应变增量     ，计算出新的应力     和雅可比矩阵 DDSDDE。这个其实也很简单。

以一阶广义Maxwell模型为例。将当前时间增量步结束时的应力记为     ，当前增量步开始时的应力记为     ，应力增量为     ；同理也有     。

把它们代入式     ，由于整个方程都是线性的，所以可以直接得到：

然后把前面的     再用这一套记法重写一遍：

从式     出发，根据偏导的定义，可知：

这样就能写出DDSDDE矩阵的分量了：

把式     ~    和前一篇黏弹性文章中推导出的列式做一个对比。因为变量记法不完全相同，我们把上一篇推送中的列式按照本文的符号记法写出来。长期模量记为     ：