小学数学应用题——水池进排水问题

本文摘要(由AI生成):
文章主要讨论了一个经典的小学数学应用题,即一个水池有一个进水管和一个排水管,只开进水管需要2小时放满,只开排水管需要6小时排空,从空水池开始同时打开进排水管,需要多长时间才能放满。文章指出,这个问题的答案并非简单的小学数学计算,而是需要运用流体力学的伯努利定律和连续方程,以及微积分方法。最终得出,同时打开进排水管需要3.9小时才能放满水池。文章还指出,实际问题总是很复杂的,本文的解答也只是一个理想化结果,实际应用中需要考虑更多因素。
水池进排水问题是经典的小学数学应用题。
导 读:经过了几篇略显烧脑的文章后,来一篇轻松一点的,经典的小学数学应用题。
1、问题分析
题:一个水池有一个进水管和一个排水管。只开进水管,2个小时可以把水池放满,之后关闭进水管,只开排水管,需6个小时可以把水池排空。问:从空水池开始,同时打开进排水管,多长时间可以把水池放满?
解:设水池的体积是“1”,则进水速度是1/2(1小时进1/2池子的水),排水速度是1/6(1小时排1/6池子的水)。
时间=体积/(进水速度-排水速度)=1/(1/2-1/6)=3 (小时)
答:需要3小时可以放满。
然而......
这个解答并不符合实际的情况,因为位于水池底部的排水管的排水速度并不是恒定的,而是和水的深度有关,具体关系式可以用伯努利定律得出。
当排水口的尺寸比水池小得多时,放水过程中水面下降速度很慢,这时可以通过伯努利定律得出排水速度为:

g为重力加速度,h为水面到排水口的深度。
其实这个关系式也可以不用伯努利定律,而是用势能与动能的转化得出:
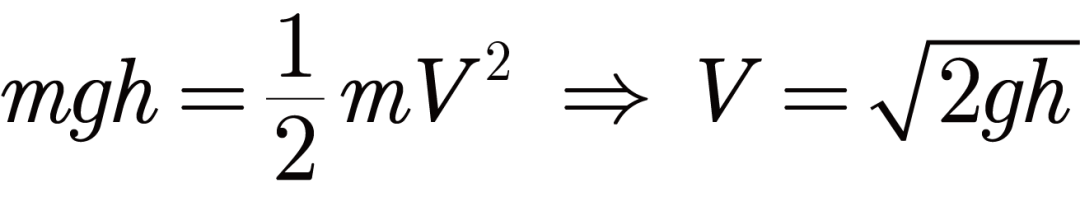
用一个可乐瓶做个实验,就可以观察到排水速度随水深变化的现象。

如果把这个题干中的“排水”明确写成用水泵抽水,就可以当小学数学题了,上面的解答也就合理了。

▲ 如果是用水泵抽水,则排水速度可以恒定。
2、正式解答:
要解答这道“小学”数学题,除了要用到流体力学的伯努利定律和连续方程外,要得到最终解还需要用到微积分方法,所以......
这里给出一种求解的过程,供大家参考。
假设只开进水,放满时间为T1,只开排水,排空的时间为T2,求同时开,放满时间T。
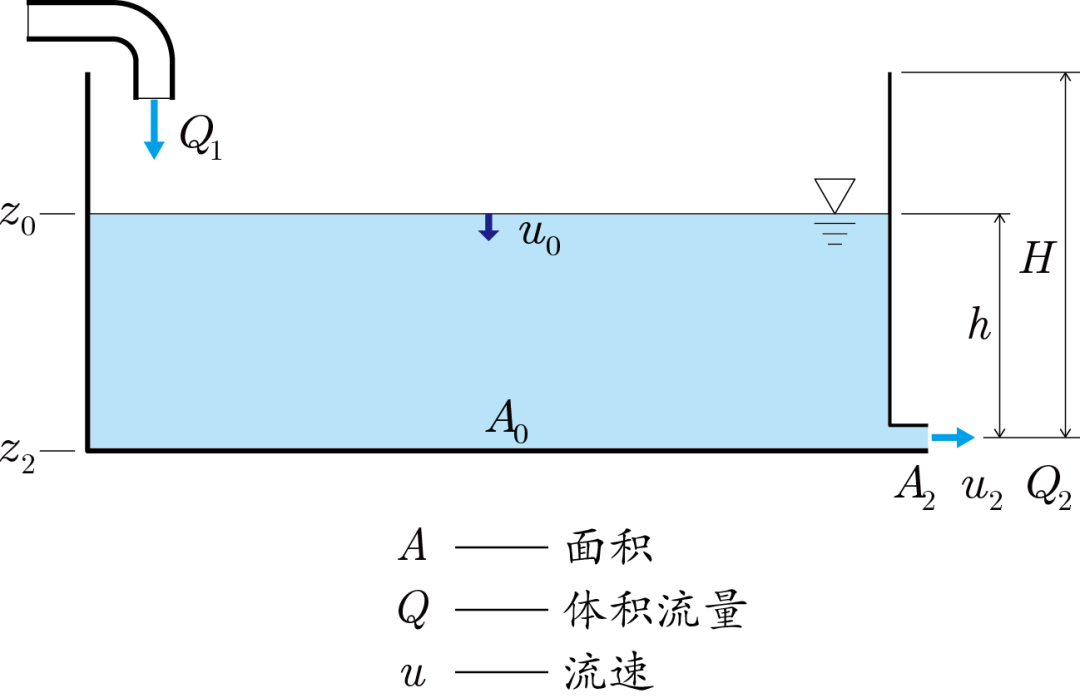
3、先看结果:
这个过程有点复杂,用了我一个下午,最终总结成了两页纸。

先来看结果吧:
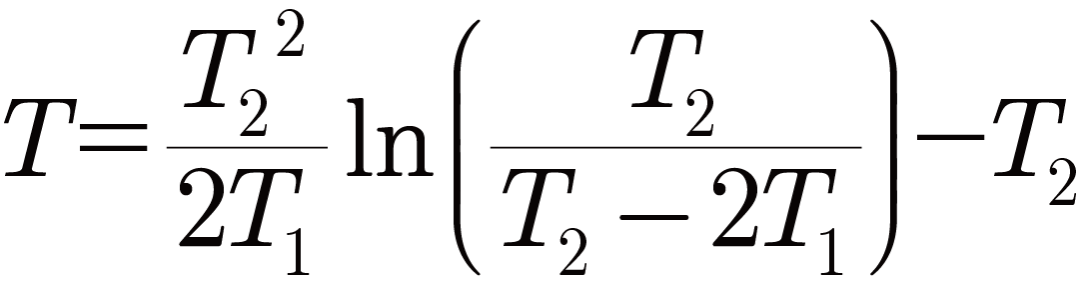
把T1=2,T2=6代入上式,得出:
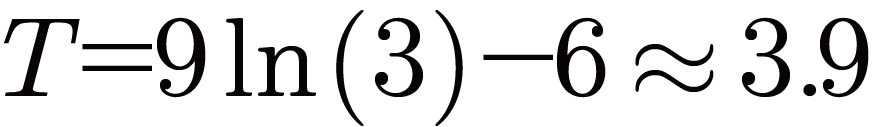
也就是说,这道数学题的答案是3.9小时,而不是小学方法得出的3小时。
4、求解过程
下面给出解题过程,感兴趣的可以看一下。


5、总结
实际问题总是很复杂的,本文的解答也只是一个理想化结果。比如实际的水池放水是不可能完全放空的,总会剩下一些。还有,放水时会出现旋涡,使水面不再是平面,这些都会影响结果。
但是,用简单的笔算,大概也只能做到这样了。完