显式仿真的网格划分策略
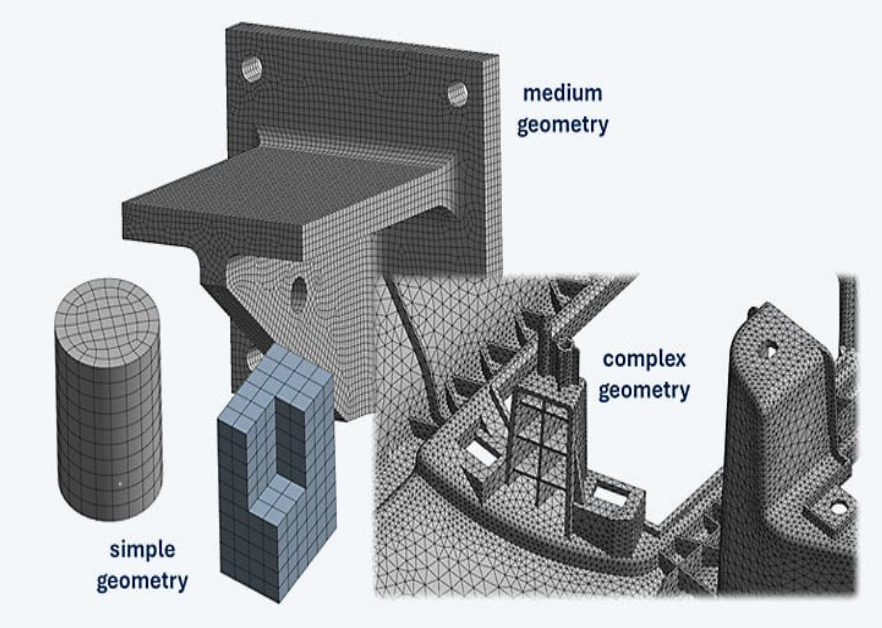
尽管由于历史原因,四面体单元,尤其是二次四面体单元常常不被认可,但它们可以成为薄壁复杂部件的解决方案。尤其对于显式仿真的新手,我们推荐使用二次单元、全局网格划分设置和自动网格特征提取等安全方法。

积分和单元类型的选择
您肯定知道求解运动方程的方法有很多种。然而,每个人都知道“隐式”方法用于线性动力学,而“显式”方法用于非线性冲击和碰撞分析?事实上,隐式方法的时间步长可以选得很大,因此它们的速度在低频范围内表现出来。显式分析本质上需要非常小的时间步长,因此波在一个时间步长内传播的距离不能超过一个单元。然而,由于公式化的原因,没有迭代方程解,因此问题的线性或非线性形式几乎无关紧要。这就是为什么显式求解器在高频范围内表现出优势,而非线性几乎是天赐之物。然而,这两个求解器基本上都可以解决所有应用。
您可能也听到过类似关于所用单元类型的“谬论”。例如,通常的做法是大幅简化模型,以便使用特殊技术将其与六面体单元进行网格划分。为了缩短计算时间,这通常需要耗费大量的工程时间。如果必须使用四面体单元,LS-DYNA 用户会避免使用二次单元,因为仅仅因为这个原因,这会使时间步长再次减半,计算时间也会加倍。
为什么我们一直这样做?因为时代需要!在(显式)仿真的早期,我们使用穿孔卡片在磁片上进行仿真,并将结果存储在磁带上。当时,工程时间比仿真时间便宜,而存储空间是昂贵的。如今,显式仿真可供众多工程师使用。我们的模型,例如复杂的注塑件,只有付出巨大的努力才能简化。这意味着,如今高效的仿真也意味着更少的模型准备工作。这种策略需要强大的网格划分工具,该工具具有许多实用的默认设置和自动化功能,还需要具有二次拟设函数的四面体。在本文中,我想用一个易于理解的示例来演示合理的网格划分策略,并提高对正确单元类型的认识。
我们应该了解的跌落测试和冲击模拟
在跌落试验中,物体从一定高度跌落,以检查冲击效果并确保物体能够承受载荷。跌落试验用于检查产品的安全性和可靠性,并可能用于改进设计或材料。有时,也会将部件夹紧,然后让试样跌落。这种(反向)跌落试验具有很高的可重复性,因此试验结果具有可比性。施加的能量可以通过冲击器的质量和速度精确控制。例如,在汽车领域,可以用这种方式模拟头部撞击。
冲击模拟基于一些简单的假设。待检查的部件或组件通常被牢固夹紧。注意:问问自己这是否允许?冲击器通常被建模为刚体,并赋予初速度。记住,跌落过程不必模拟,可以用初速度代替。初速度可以根据能量平衡简单地计算如下:
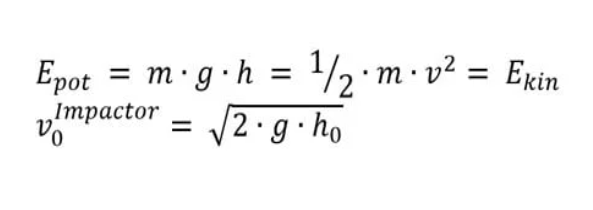
因此,可以记住,跌落高度 h=1m 时,v0=4.429 m/s。最后,您需要确定正确的结束时间。在我们的示例中,20ms 就足够了。然而,这在很大程度上取决于结构的刚度和冲击器的能量。
最后,同样重要的是,简要说明一下网格细度。这通常与结构的纯变形行为和(保持)力有关。在这种情况下,相当粗的网格就足够了,并且必须能够单独表示刚度和振动行为。如果应力或例如塑性应变起着重要作用,则需要进行额外的局部细化。结果变量因应用而异,并且取决于您在模拟中提出的具体问题。固定件是否会“脱落”或销钉是否会从结构上脱落?
Ansys LS-DYNA 中显式仿真的正确网格划分
如果您处理过显式仿真,就会注意到有些事情有所不同。例如,在 Ansys LS-DYNA 中,二次位移 Ansatz 并不一定意味着单元具有中间节点。此外,还有一些单元针对特定载荷场景进行了速度调整。您听说过有限元模型中的质量缩放吗?由于模型中的计算时间步长基于最小单元,因此通过局部增加密度可以最小化声速,从而最大化允许的时间步长。最后,重要的是要理解显式网格划分不仅仅是简单的网格划分,而是一个迭代过程。用户必须在网格划分工作量、质量缩放、所需的结果质量和计算时间之间找到有效的平衡。
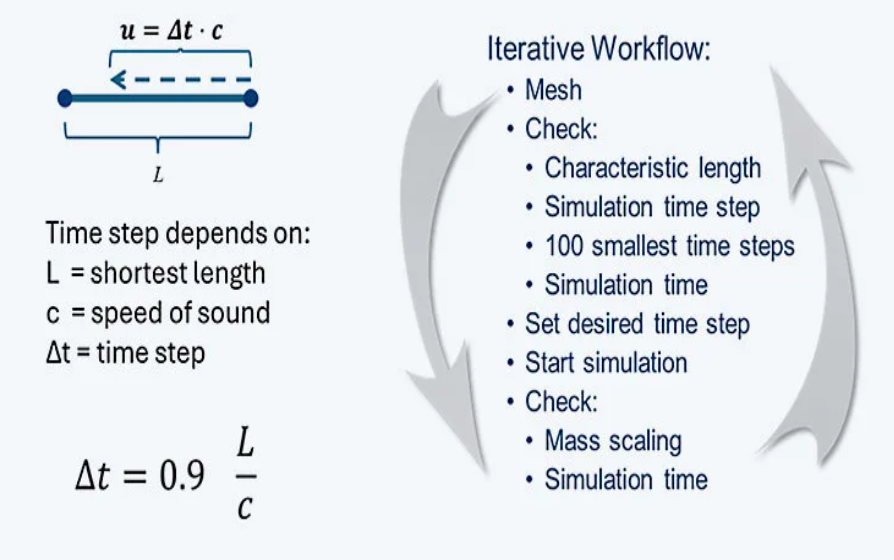
对我来说,以下方法效果很好。我先从粗网格开始,让模型“运行”。我可以设置此模型的结束时间,并检查边界条件。一旦模型稳定,我就可以细化网格,直到位移场和动态行为能够正确显示。最后,我会细化局部点,以便更好地解析局部刚度或局部评估应力和应变。我根据几何形状和数值调整第一个网格,并遵循以下经验值。纵横比不应超过 1-3,最大值为 1-5。对于薄壁部件,通常沿厚度方向使用 1 个单元就足够了;建议使用二次单元(Tet4 或 Tet16)。
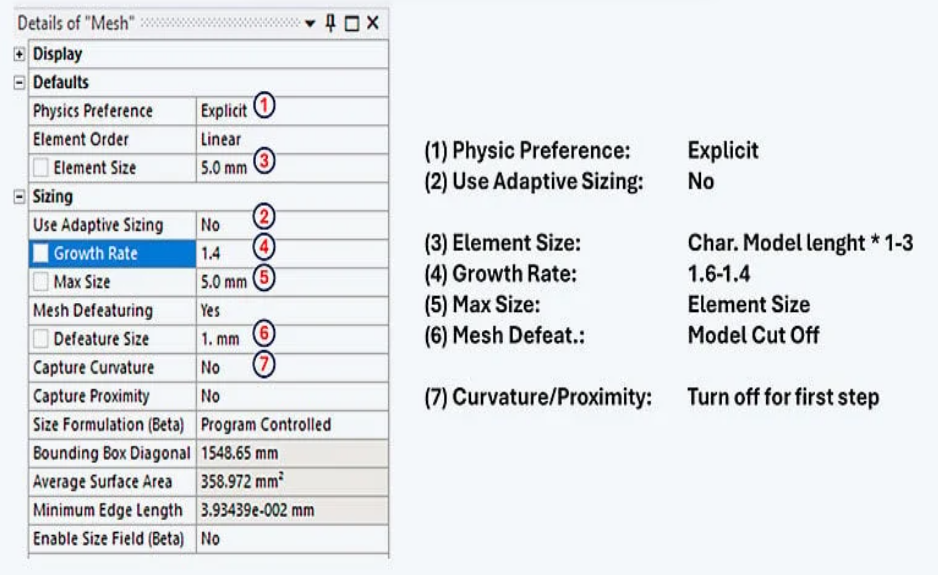
10-15年前,当我开始进行显式模拟时,为了快速生成六面体网格,我也会花费数小时甚至数天的时间简化几何结构、移除半径并切割组件。但如今,我通常会采取一种更加务实的方法。虽然良好的四面体网格比等效的六面体网格计算时间更长,但它通常更容易、更快速地生成,并且在结果质量方面也丝毫不逊色于六面体网格。此外,四面体网格可以应用于最复杂的几何结构,并且全局设置通常足以控制整个网格。此外,我并不喜欢快速但“不精确”地达到目标。我更喜欢使用二次单元让模型运行更长时间,但我可以信赖更好的结果质量。
碰撞、跌落、变形:高度非线性任务的模拟
LS-DYNA 适用于模拟具有大变形、稳定性问题和最复杂接触场景的非线性过程
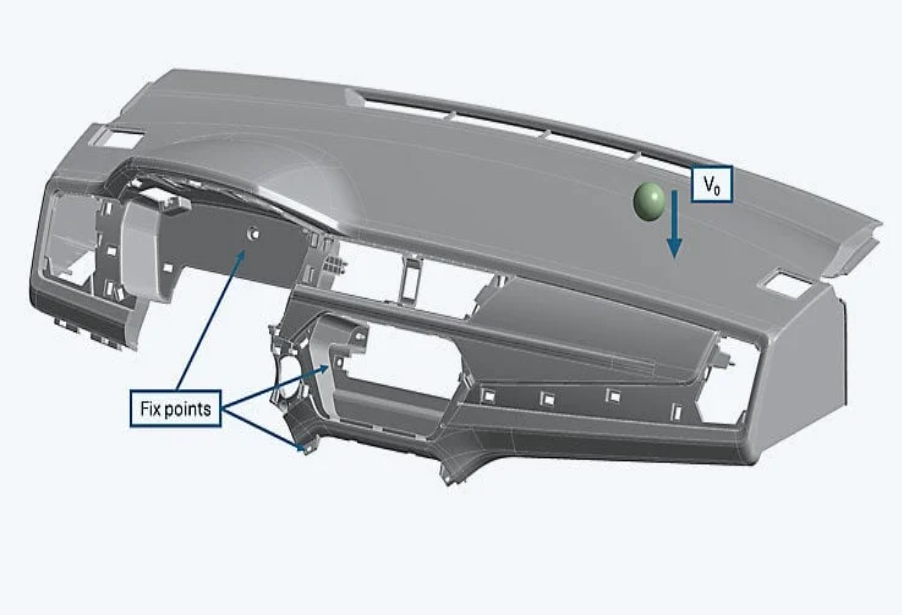
车辆仪表板的撞击模拟
举个例子,我们来看看对车辆仪表板的撞击。重 1kg 的物体从一米高处落到一个恰好“柔软”且柔顺的点上,因此我们生成了一个以弯曲为主的载荷工况。因此,我们使用了撞击器的位移。该结构采用之前显示的默认设置进行网格划分,包含约 420,000 个四面体单元。
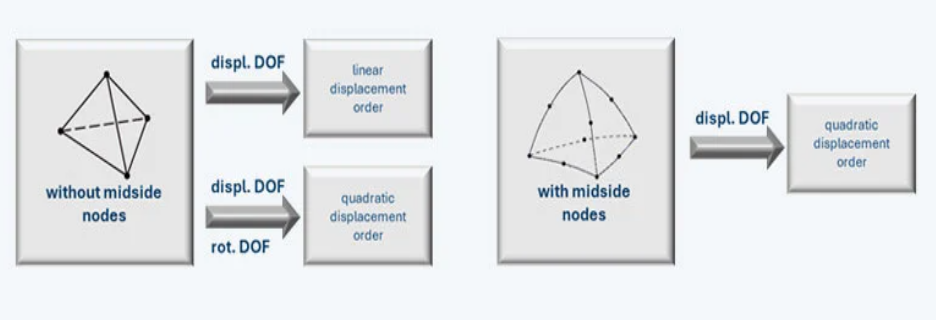
比较了四种元素类型:
Tet10: 线性,默认
快速但非常坚硬的元素,仅适用于泊松比较低的材料。Tet13: 线性,附加压力自由度
适用于泊松比较高的材料(超弹性或塑性)Tet4: 一阶单元,无中间节点,附加旋转自由度
推荐用于薄壁结构Tet16: 二阶单元,具有中间节点
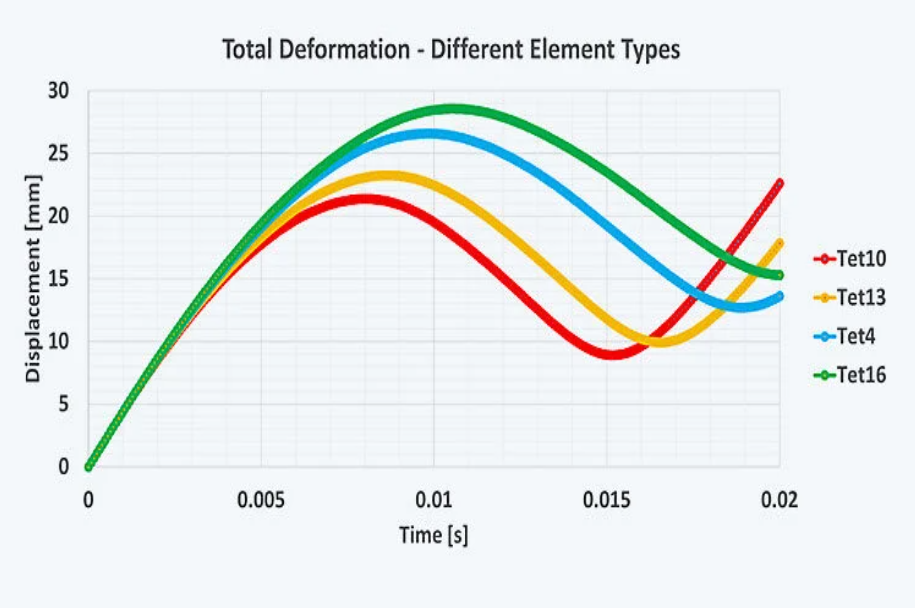
图中可以清晰地看出单元公式的差异。冲击器位移行为的偏差高达 30%,这导致 Tet10 性能较差,而 Tet16 性能更佳。(准)二次 Tet4 的性能也相当不错,但偏差明显。Tet10 和 Tet13 的结果相似,其中 Tet13 的设计适用于泊松数接近 0.5(超弹性或塑性)的情况。因此,静水压力的额外自由度在弯曲主导载荷工况下几乎没有任何优势。在 Tet10、Tet13 和 Tet4 采用相同网格,Tet16 采用相同节点数的情况下,计算时间(相对于 Tet10)存在以下差异:Tet13 为 1.6,Tet4 为 1.75,Tet16 为 9。由于 Tet16 具有更多节点,我们可以将网格划分粗化两倍,最终结果仅为约 5 倍。
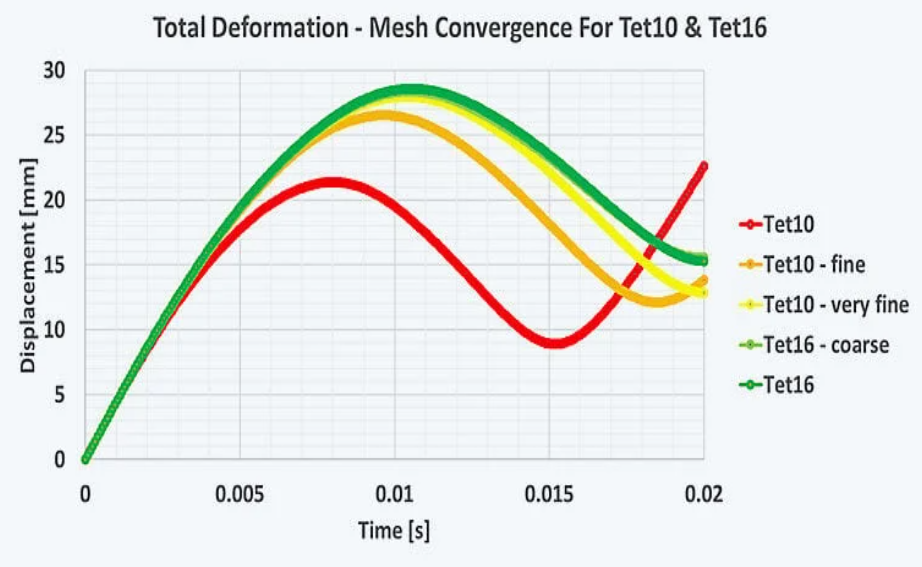
当然,使用 Tet10 也能取得不错的效果。但遗憾的是,网格必须非常精细。在我们之前示例中,如果沿厚度方向设置 3 个单元,最终得到的单元数量将是之前的 30 倍!
结论: 标准四面体单元 Tet10 计算速度最快,但偏差也最大。Tet13 和 Tet4 均具有特殊属性,适用于某些载荷场景,并在计算时间和结果质量之间取得平衡。然而,用户必须了解哪种单元适用于哪种场景。Tet16 的计算时间更长,但结果最佳。别忘了,您也可以使用更粗的网格划分,同时保持相同的结果质量。
总结与建议
您是否处理过复杂的、可能是薄壁的部件?那么以下几点或许对您有所帮助。显式仿真的网格划分通常是一个迭代过程。与其他类型的仿真一样,必须定义合适的网格密度才能以所需的精度获得所需的结果。
此外,为了确保稳定性和效率,必须考虑时间步和质量缩放。四面体网格通常可以通过一些全局设置生成,并且网格生成器可以轻松进行网格去除.
对于薄壁部件,应使用二次单元。由于 LS-DYNA 中默认的线性四面体单元设计注重速度而非精度,因此用户应切换到二次单元。
没有中间节点但具有额外自由度(Tet4)的单元可以在速度和精度之间取得平衡。这些建议旨在提高模拟的效率和精度,并帮助您在不影响模拟稳定性和效率的情况下获得最佳结果。通过使用正确的单元和网格划分方法,您可以确保模拟既快速又准确。





