角谱衍射计算:从理论到MATLAB实现的全解析【附代码】
1 引言:光学仿真的挑战与突破
在数字全息、光学干涉测量和衍射光学元件设计等前沿研究领域,光学衍射过程的准确仿真一直是一个关键的技术挑战。传统的基于标量衍射理论的数值计算方法,如菲涅尔衍射积分和夫琅禾费衍射,往往面临一个根本性限制:抽样间隔必须随传播距离变化。
这一限制严重影响了衍射光学元件设计的效率和精度。本文将深入解析角谱衍射理论的核心原理,详细讲解近场与远场算法的数学基础,文章最后模拟计算圆孔衍射屏在不同衍射距离处的衍射图像。并提供完整的MATLAB实现代码,为光学研究者提供一套完整的技术参考方案。
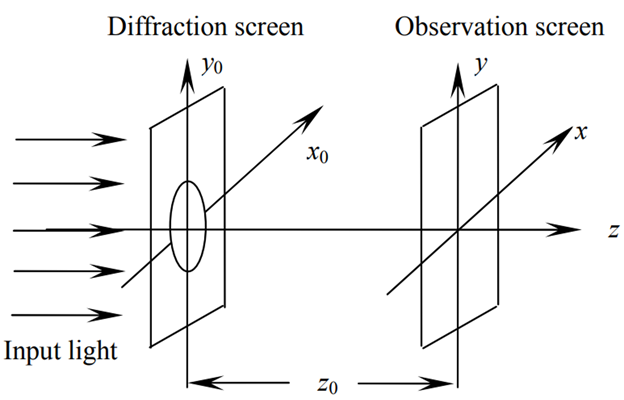
图 1圆孔衍射示意图
2 角谱理论:从物理概念到数学表达
2.1 理论基础:平面波角谱分解
角谱理论的核心物理思想是将任意光场分解为不同传播方向的平面波。这一过程可以理解为光学领域的“傅里叶分析”:
空间域到频域:将输入平面的光场复振幅分布分解为不同空间频率的平面波分量
传播过程:每个平面波分量在自由空间中独立传播,经历不同的相位延迟
频域回空间域:在输出平面重新合成所有平面波分量,得到衍射图样
2.2 数学表达:连续形式的角谱理论
角谱理论的完整数学描述包含三个核心方程:
角谱分解(空间域→频域)
角谱传播(频域传播)
角谱合成(频域→空间域)
2.3 传递函数与点扩散函数的关系
角谱理论有两种等价的数学表达形式:
频域传递函数:
空域点扩散函数:
3 离散化实现:从理论到算法的关键步骤
3.1 离散傅里叶变换的约束
在实际的计算机仿真中,连续的傅里叶变换必须离散化为DFT(离散傅里叶变换):
空域-频域抽样关系:
3.2 特征距离:算法选择的关键判据
特征距离d是角谱算法中最重要的参数:
这个参数决定了近场算法和远场算法的适用边界:
当传播距离 z ≤ d 时,适用近场算法 当传播距离 z ≥ d 时,适用远场算法 当 z = d 时,两种算法等价
4 算法实现:近场与远场的分工协作
4.1 近场算法(基于传递函数)
近场算法直接在频域中操作,通过传递函数实现角谱传播。
算法流程:
对输入光场进行FFT,得到角谱分布 构造角谱传递函数 在频域进行角谱传播 通过IFFT重建输出光场
4.2 远场算法(基于点扩散函数)
远场算法在空域中通过卷积定理实现衍射计算。
算法流程:
构造点扩散函数(空域) 对输入光场和点扩散函数分别进行FFT 在频域进行乘法运算(等价于空域卷积) 通过IFFT得到输出光场
卷积定理的应用:
5 完整MATLAB实现代码
.rtcContent { padding: 30px; } .lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }clear all;close all;clc;%% 参数设置lambda = 632.8e-9; % 波长N = 1064; % 采样点数dx = 10e-6; % 采样间隔D = 5e-3; % 圆孔直径% 计算特征距离dd = N * dx^2 / lambda;fprintf('特征距离 d = %.2f mm\n', d*1000);% 传播距离设置 (0.5d, d, 5d)z_values = [0.5*d, d, 5*d];%% 创建圆孔衍射屏[x, y] = meshgrid((-N/2:N/2-1)*dx);r = sqrt(x.^2 + y.^2);Uin = double(r <= D/2); % 圆孔% 显示输入场figure;imagesc(x(1,:)*1000, y(:,1)*1000, Uin);axis image; colormap gray;xlabel('x (mm)'); ylabel('y (mm)');title('输入场 - 圆孔衍射屏');colorbar;%% 近场算法计算figure('Name', '近场算法结果');for i = 1:3z = z_values(i);Uout_near = ASM_Near(Uin, lambda, z, dx);% 计算强度I_near = abs(Uout_near).^2;% 计算输出平面的坐标x_out = x;y_out = y;% 显示结果subplot(1, 3, i);imagesc(x_out(1,:)*1000, y_out(:,1)*1000, I_near);axis image; colormap jet;xlabel('x (mm)'); ylabel('y (mm)');title(sprintf('z = %.1f mm\n(%.1fd)', z*1000, z/d));colorbar;endsgtitle('近场算法模拟结果');%% 远场算法计算figure('Name', '远场算法结果');for i = 1:3z = z_values(i);Uout_far = ASM_Far(Uin, lambda, z, dx);% 计算强度I_far = abs(Uout_far).^2;% 计算输出平面的坐标x_out = x;y_out = y;% 显示结果subplot(1, 3, i);imagesc(x_out(1,:)*1000, y_out(:,1)*1000, I_far);axis image; colormap jet;xlabel('x (mm)'); ylabel('y (mm)');title(sprintf('z = %.1f mm\n(%.1fd)', z*1000, z/d));colorbar;endsgtitle('远场算法模拟结果');%% 近场算法function Uout = ASM_Near(Uin, lambda, z, dx)% Uin: 输入复振幅场% lambda: 波长% z: 传播距离% dx: 输入平面的采样间隔[Ny, Nx] = size(Uin);k = 2*pi/lambda;% 生成空间频率坐标fx = (-Nx/2 : Nx/2-1) / (Nx * dx);fy = (-Ny/2 : Ny/2-1) / (Ny * dx);[Fx, Fy] = meshgrid(fx, fy);% 角谱传递函数HH = exp(1i*k*z*sqrt(1 - (lambda*Fx).^2 - (lambda*Fy).^2));H(real(sqrt(1 - (lambda*Fx).^2 - (lambda*Fy).^2)) < 0) = 0;H = fftshift(H);du = 1/(Nx * dx); % 频率域采样间隔dv = 1/(Ny * dx);% 角谱衍射U_spectrum = fft2(fftshift(Uin)) * (dx * dx);Uout = fftshift(ifft2(U_spectrum .* H)) * (du * dv * Nx * Ny);Uout = Uout .* exp(1i*k*z);end%% 远场算法function Uout = ASM_Far(Uin, lambda, z, dx)% Uin: 输入复振幅场% lambda: 波长% z: 传播距离% dx: 输入平面的采样间隔[Ny, Nx] = size(Uin);k = 2*pi/lambda;% 生成空域坐标x = (-Nx/2 : Nx/2-1) * dx;y = (-Ny/2 : Ny/2-1) * dx;[X, Y] = meshgrid(x, y);% 点扩散函数h = exp(1i*k*z) / (1i*lambda*z) .* exp(1i*k/(2*z) * (X.^2 + Y.^2));% 卷积U1 = fft2(fftshift(Uin));U2 = fft2(fftshift(h));Uout = fftshift(ifft2(U1 .* U2));Uout = Uout * dx^2;end
6 算法性能分析与验证
6.1 计算精度验证
波长为 632.8 nm,衍射屏由1064pixel×1064pixel构成,抽样间隔为Δx0=Δy0=10 μm,圆孔直径等于3.5mm,d=81mm。通过对比不同传播距离下的仿真结果,我们可以系统验证算法的准确性:
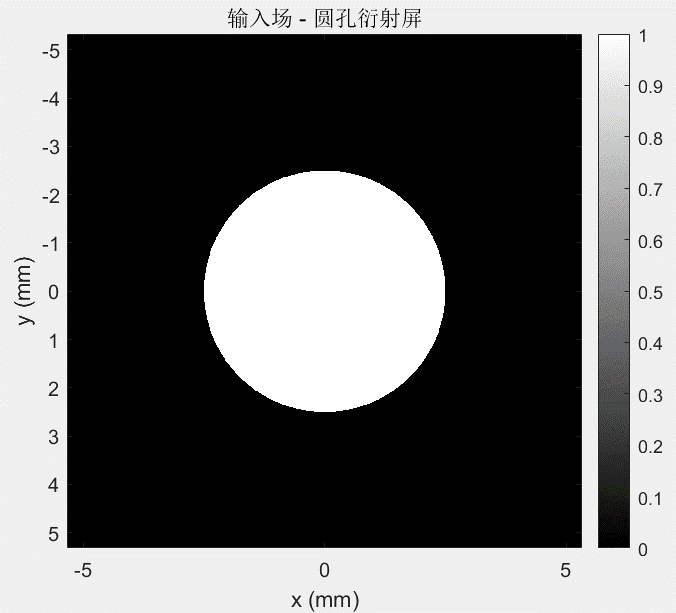
图2 圆孔衍射屏
z = 0.5d(近场区域)
近场算法:衍射图样边缘清晰,分辨率高
远场算法:开始出现轻微的分辨率下降
z = d(特征距离)
两种算法结果高度一致
验证了特征距离理论的正确性
衍射图样开始展现典型的菲涅尔衍射特征
z = 5d(远场区域)
远场算法:保持较高的图像质量
近场算法:分辨率明显下降,出现混叠现象
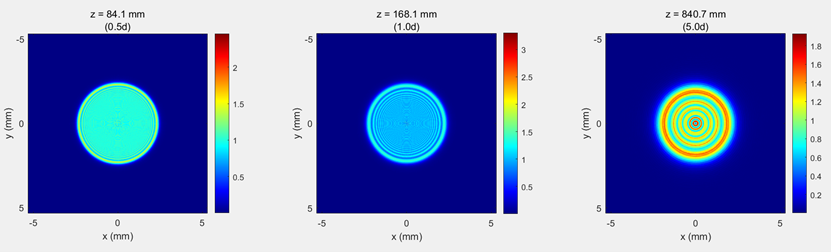
图3近场算法计算结果
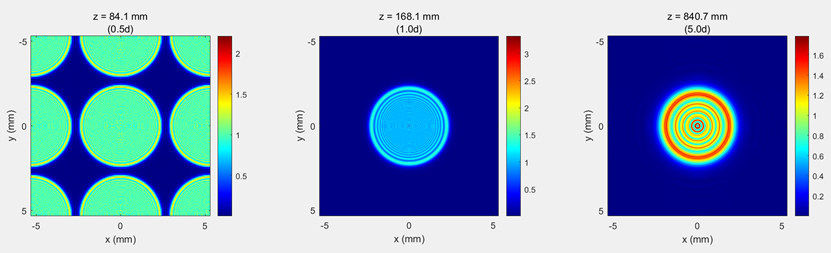
图4远场算法计算结果
6.2 计算效率分析
角谱算法的计算复杂度主要由FFT决定:
单次FFT计算复杂度:O(N²logN)
近场算法:2次FFT(正变换+逆变换)
远场算法:3次FFT(输入场变换+点扩散函数变换+逆变换)





