优化分析为什么不能打开大变形
简单来说,不能打开大变形”的根本原因是:分析的基本假设和方程在几何非线性条件下不再成立。 强行在不支持的分析中打开大变形,会导致结果完全错误、不收敛,甚至让分析无法进行。
下面我们从几个层面进行优化分析,详细解释为什么。
一、核心概念:小变形 vs. 大变形
首先,要理解两者的根本区别:
小变形假设:
平衡方程建立在未变形的初始构型上。
应力-应变关系是线性的(胡克定律)。
所有计算(如单元刚度矩阵)在分析开始前就一次性计算完成,并且在分析过程中保持不变。
这是一种线性分析,计算速度快,资源消耗少。
核心思想: 结构在载荷作用下发生的变形和位移非常小,不足以显著改变结构的刚度、形状或受力方向。
大变形假设:
平衡方程必须跟随结构变形,建立在不断更新的当前构型上。
需要考虑几何非线性效应,如应力刚化(薄膜效应)、旋转软化等。
单元刚度矩阵需要在每个载荷步或迭代步中根据当前的变形状态重新计算。
这是一种非线性分析,计算复杂,耗时且资源密集。
核心思想: 结构发生的变形和位移很大,足以显著改变结构的刚度、几何形状和载荷路径。
分析特点:
平衡方程必须跟随结构变形,建立在不断更新的当前构型上。
需要考虑几何非线性效应,如应力刚化(薄膜效应)、旋转软化等。
单元刚度矩阵需要在每个载荷步或迭代步中根据当前的变形状态重新计算。
这是一种非线性分析,计算复杂,耗时且资源密集。
二、为什么“不能”随意打开大变形?—— 从后果角度分析
当你在一个本应使用小变形假设的模型中打开大变形选项时,会引发一系列问题:
1. 物理上的不合理性(结果错误)
这是最致命的问题。如果实际情况是小变形,你却用大变形理论去计算,会引入本不存在的非线性效应,导致结果失真。
案例: 一个简单的悬臂梁,在端部施加一个微小载荷。小变形分析会给出一个微小的、线性的位移。如果打开大变形,求解器会去考虑梁弯曲后力臂的变化,从而计算出与线性结果不同的位移和应力。然而,在微小载荷下,这种几何变化的影响微乎其微,大变形分析得到的结果虽然是“精确”的非线性解,但它与真实的、被广泛验证的线性解有微小差异,对于追求精确线性解的工程师来说,这反而是“错误”的。
2. 数值计算上的困难(不收敛)
大变形分析是一个非线性过程,求解器通常采用迭代法(如牛顿-拉夫森法)。
收敛性问题: 对于一个小变形问题,其力-位移关系本质是线性的。如果强行用非线性的迭代算法去求解一个线性问题,可能会遇到不必要的收敛困难,甚至迭代发散。这好比用求解二次方程的公式去解一个一元一次方程,不仅多此一举,还可能因为数值精度问题得不到正确答案。
计算成本飙升: 大变形分析需要在每个子步都重新形成刚度矩阵并进行求解,计算量远大于小变形分析。对于一个本可用简单方法快速解决的问题,这是一种巨大的资源浪费。
3. 模型设置的限制(分析失败)
某些分析类型或单元类型天生就与小变形假设绑定,不支持几何非线性。
特征值屈曲分析: 经典的线性屈曲分析基于小变形假设,它通过线性推演来预测屈曲载荷。在此分析中打开大变形是无意义的,因为大变形是屈曲之后的现象。
特定单元: 一些简化单元(如某些类型的弹簧单元、接触单元)可能只在小变形框架下开发,其公式不支持有限转动或大应变。
载荷类型: 跟随力(方向随结构变形而改变的力)只在大变形分析中才有意义。在小变形分析中,所有力的方向都被认为是固定的。如果模型中有本应是跟随力的载荷,却在小变形分析中运行,会导致载荷施加错误。
三、决策流程图:什么时候应该打开大变形?
你可以根据以下流程图来判断你的分析是否需要打开大变形:
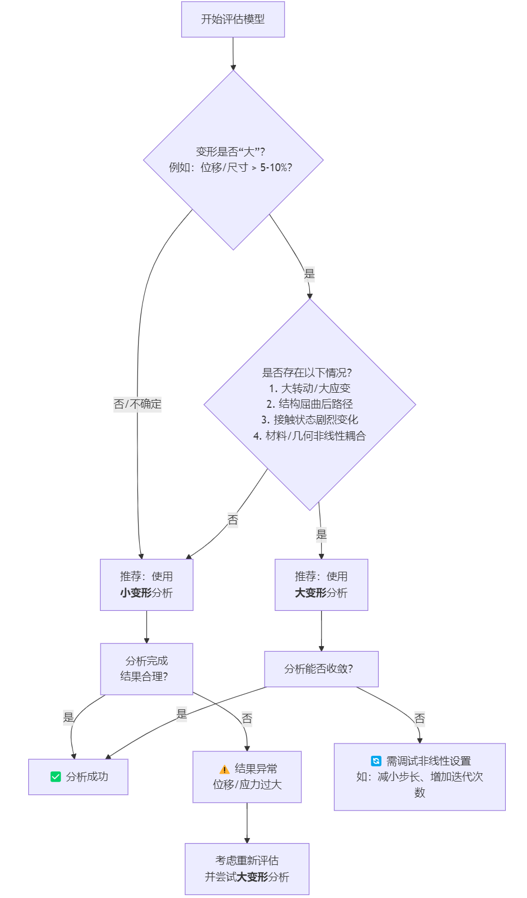
四、典型必须开启大变形的案例
橡胶密封圈的压缩: 应变可能超过50%,几何形状发生巨大改变。
钓鱼竿的弯曲: 虽然材料是线性的,但会发生大位移、大转动,载荷方向和结构刚度显著变化。
薄膜结构的充气过程: 从松弛状态到张紧状态,经历巨大的几何变化和应力刚化。
手机铰链的翻折: 涉及大转动和复杂的接触行为。
结构的后屈曲分析: 研究结构在失稳后能否继续承载。
总结
| 物理假设 | ||
| 计算基础 | ||
| 计算效率 | 高 | 低 |
| 结果精度 | ||
| 关键选择 | 默认、首选 | 需要时启用 |
最终建议:
在进行任何分析时,首先应该默认使用小变形设置。只有当你有明确的理由相信模型会发生大变形,或者小变形分析得到了不合理的大位移/大应变结果时,才应该考虑打开大变形选项,并准备好应对更长的求解时间和可能的收敛性问题。
网络资源,仅限内部分享,禁止商用





