有限元基础知识:模态参与因子与有效质量
之前讲了很多关于模态分析的知识,但是有朋友反馈我缺少了模态有效质量与参与因子这些部分,今天就给大家补上。之前说的模态分析相关的可以回看:
模态有效质量和模态参与因子是结构动力学分析中的两个核心概念,主要的作用在于理解结构的哪些模态对结构响应起关键作用,两者又经常结对使用。总结如下:
| 模态参与因子 (Modal Participation Factor) | 模态有效质量 (Modal Effective Mass) | |
|---|---|---|
| 物理意义 | ||
| 主要用途 |
下边具体说一下他们的计算
模态参与因子的计算与意义
模态参与因子定量描述了在特定方向(如X向平动或绕Z轴转动)的激励下,某一阶模态被激发出来的“意愿”有多强。其计算公式为:
其中, 为第i个振型, 是结构的质量矩阵, 是 方向(如X向)的激励方向向量(表示该方向发生单位刚体 位移时,各自由度产生的位移)。比如说对于一个4个节点的系统,x为激励方向,那么 ,非常的简单清晰。那么可以看到一个矩阵前边乘一个向量,后边乘一个向量得到的结果就是个标量,这个标量:
值的大小:绝对值越大(注意这里是绝对值,因为参与系数可正可负,振型其实是特征向量归一化后的结果,整体乘个 没影响),表示该模态在对应方向的动力响应中贡献越大。 模态有效质量的计算与意义
你可以把它想象成在某个振动方向上,每一阶模态单独“掌管”了多少质量。它的计算公式直接与模态参与因子相关,所以这也是为啥他俩一般结对出现,算完参与因子,顺利成章算算有效质量:
其中 为第 阶模态对应的广义质量,写作 , 由于我们在有限元中一般都是归一化后再做处理,所以一般就是1.0,那这时候模态有效质量就直接等于参与因子的平方。
核心原则:在一个特定方向上,所有模态的有效质量之和等于结构的总质量(平动)或总转动惯量(转动)。这一性质被称为有效质量守恒。
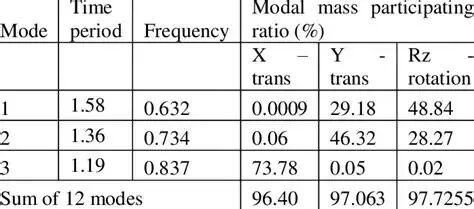
用处:由于这个性质的存在,使得有效质量成为判断模态分析是否提取了足够阶数的黄金准则。例如,在进行响应谱分析或瞬态动力学分析(采用模态叠加法)时,通常会要求所提取模态在主要激励方向上的累计有效质量占比(即前N阶模态有效质量之和与总质量之比)达到80%甚至90%以上,由于总的质量是一定的,所以选取一定阶数的振型,才能保证计算精度。
场景
识别主导模态:通过比较各阶模态的参与因子或有效质量,可以快速识别出在特定载荷工况下对结构响应贡献最大的模态,从而进行针对性的优化或控制。
判断模态提取充分性:利用累计有效质量百分比,科学地确定需要提取多少阶模态才能满足后续动力学分析的精度要求,避免盲目提取过多或过少。实现效率与精度的平衡。
指导结构设计:如果发现某阶不希望被激励起来的模态(其频率与工作频率接近)具有很高的有效质量,就意味着需要改变结构的刚度或质量分布以规避共振风险。





