技术干货 | Ansys HFSS求解阶数与矩阵求解算法介绍
1、前言
我们在使用Ansys HFSS时经常会碰到Setup设置问题,许多使用者对Setup设置项有疑惑,不知道该如何设置。本文对Setup中的求解阶数和矩阵求解算法做个介绍,希望能帮助到大家在今后求解设置时根据仿真场景更准确的选择对应设置。
2、Ansys HFSS Setup求解阶数
Ansys HFSS利用有限元算法剖分网格并计算每个四面体的场,并形成了与每个四面体相关联的基函数。基函数是n阶多项式,它描述了电场如何沿着四面体的边、面或体发生变化。
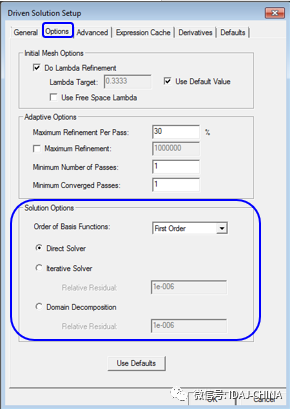
在HFSS Setup中,Solution Options给出了四种求解阶数选择如下:
(1)Zero Order零阶,每个四面体6个未知量
(2)First Order一阶,每个四面体20个未知量
(3)Second Order二阶,每个四面体45个未知量
(4)Mixed Order混合阶,根据模型不同部分对更高精度的要求分配基函数
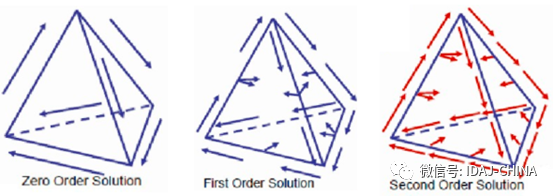
HFSS电磁场有限元求解采用四面体网格剖分,在每个网格上求解Maxwell方程组。求解时间与网格数量、由网格生成的矩阵大小、矩阵的稀疏程度相关。
我们来看一个Patch Antenna例子。
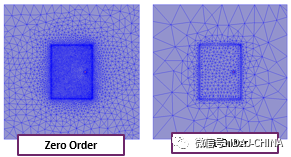
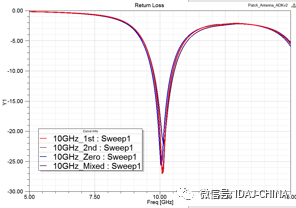
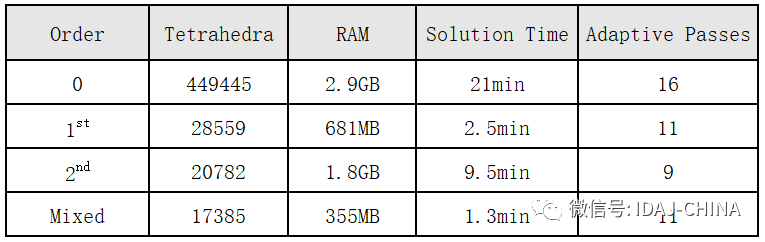
采用不同阶数的基函数求解都得到了几乎相同的结果。通常,高阶基函数需要较少的自适应迭代次数达到收敛。如果网格密度减少,一个问题将需要更少的内存来求解。理想基函数的选择与仿真场景有关。
要根据计算模型的具体情况进行阶数选择,一阶求解(默认)适合于大多数情况;高阶基函数需要更少的四面体来精确描述场,所以对于大而均匀的结构,二阶网格更大,相应的网格数量少、矩阵小,计算效率更高;对于结构复杂而电尺寸较小的结构,低阶求解效率更高。


求解阶数设置的一般性原则如下图示。
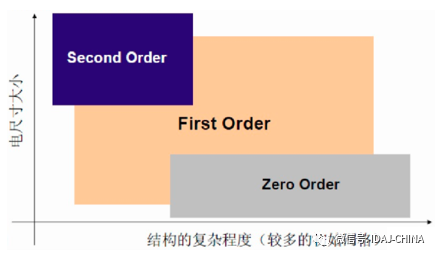
在求解时,可通过Profile观察网格数量、矩阵大小、求解时间、内存消耗等进行比较,积累经验。
3、Ansys HFSS矩阵求解算法
每次HFSS求解场时,它都必须求解一个未知矩阵Ax=b。HFSS提供三个求解器选项来应用于这个矩阵方程求解。
(1)Direct Solver直接法,这是HFSS使用的传统求解器;
(2)Iterative Solver迭代法;
(3)Domain Decomposition区域分解法,它允许单个求解利用跨网络的分布式RAM来并行求解,它可以将网格子域分配到计算机网络中的不同处理器,显著增加仿真能力;
直接法和迭代法对比如下:
Direct Solver
(1)直接求解矩阵,相比迭代法消耗更多内存;
(2)求解稳定,不存在收敛性问题;
(3)适合中小规模矩阵;
Iterative Solver
(1)适合中大规模矩阵求解,内存消耗少;
(2)在内存资源一定的情况下,求解更大规模的问题;
(3)求解不收敛时,自动切换回直接法矩阵求解器;
直接法和迭代法内存消耗比较:
(1)Direct Solver:未知量N的1.2~1.3次方;
(2)Iterative Solver:未知量N的1.0~1.1次方,接近线性;
Iterative Solver的选择原则:
(1)对于物理内存较小的计算机,求解端口数量较少的问题,迭代法速度提高明显;
•端口数少于CPU数量的两倍时:迭代法
•端口数大于CPU数量的两倍时:直接法
(2)迭代法不收敛则自动采用直接法求解;
• 网格数量增加,迭代法的收敛性会改进;
(3)快速扫频(Fast Sweep)与矩阵算法;
•未知量在10万以下:Direct Solver效率高;
•未知量在30万以上:Iterative Solver效率高;





