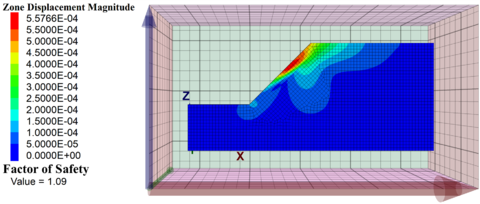
数值分析做好边坡稳定性的关键心得分享

1月前浏览35

数值分析区别于极限平衡法，极限平衡法不考虑边坡模型的应力应变情况，而数值分析结果会呈现不同的应力应变结果，这也是大家一直在论文中提到的“数值优势”，但如何做好边坡稳定性的数值分析呢？我认为有以下几点：

（1）基础数据的准确性是最重要的一环，定性判断永远是做好边坡分析的第一步，地勘钻孔的布设，物理力学参数的选取，这些所占边坡分析报告的篇幅我认为不应该低于20％，应该要详细论述我为什么选择这个断面作为计算模型，相关的物理力学参数为什么这么选取应说出一个完整的体系来，如附近的高边坡坡率如何、现状稳定性怎样、是否有病害、采用了何种支护形式，拟建高边坡钻孔取样试验结果如何，代入到既有高边坡中的稳定性结果怎样，和实际现状是否相符，这都是判断参数合理性的有效手段。

（2）数值分析中位移到底怎么看，数值分析计算边坡稳定系数的主要实现手段是强度折减法，那么强度折减法计算出的稳定系数明明很高，但位移大的出奇，比如一个1:1坡率10m高的边坡，c值30kpa，φ值20°，计算结果为1.652，最大位移接近10m，跟实际是相悖的，那么我们换一个思路，对其单独进行弹塑性分析，计算平衡后即为其现状位移，根据定性判断位移值肯定是少之又少，这样的话我们就要考虑模型位移的真正适用情况，我建议对于稳定系数在1.05以下的边坡，即欠稳定边坡，分析其破坏时的位移是有必要的，但对于稳定性较高的边坡分析其破坏时候的位移没有太大的意义，分析方式有两种一种是直接进行弹塑性分析，另外一种是将抗剪强度指标按稳定系数折减后进行弹塑性分析，前者分析的是现状位移，后者分析的是当边坡处于极限平衡时其位移的情况。

（3）边界尺寸的确定是建立数值模型的重要准备工作，边界尺寸的大小影响模型的应力应变分布，至今学者们没有统一的边界条件选取依据，极限平衡法计算模型相比于数值计算模型边界尺寸的要求并不高，只要滑动面在边界之内就可以得到准确的结果，但由于数值计算模型需要考虑其整体的应力应变分布情况，因此必须要考虑边界效应的影响。我在《公路交通科技》中发表的论文《土质边坡数值模型稳定性的求解精度研究》对边界尺寸进行了详细研究，最终建议坡脚至下边界尺寸U不小于0.75H，右边界至坡顶边界尺寸R不小于2H，左边界至坡脚边界尺寸L应小于1H。

（4）关于网格尺寸，现在用optum比较多，网格都采用的是模型自适应网格，划分极为便捷且准确，一般的软件网格需要自行划分，这就很影响计算精度，目前模型网格尺寸划分主要存在的问题集中于网格尺寸大小的确定，一个普通的边坡模型，网格采用1m×1m网格与0.5m×0.5m网格计算结果可以相差10％以上，但目前通常的做法是根据模型的尺寸选取一个中等网格尺寸进行划分求解，逐渐加密直至计算结果相差不大时，将此状态下的网格大小作为模型的最终网格尺寸，但此方法耗费时间较长，且要经若干次的网格划分才能得到。在论文中我也进行了研究，坡体区域每平米网格数为4个时，每个边坡模型的稳定系数与极限平衡法计算结果是最为接近的，平均误差仅2.31％，计算精度较为理想，平均耗时约10min。当坡体区域每平米网格数为2个时，每个边坡模型的稳定系数与极限平衡法计算结果的平均误差为5.03％，平均耗时4min。其他划分形式下的边坡模型由于网格较为稀疏，虽然耗时均在1min以内，但因计算结果误差较大导致结果精度较低。因此，建议在边坡模型中，划分网格时应逐线划分，坡体区域每平米划分应不小于4个网格，相应不小于5个节点，当精度要求不太高且模型较大时，可将距离坡体区域每平米划2-4个网格，远离坡体的区域应采用尺寸变化梯度过渡增大，该区域网格对于边坡模型的稳定系数影响不大，但由于各区域网格节点需要较完美的衔接，因此变化梯度不应过大，建议一般边界区域的网格个数取边坡坡体区域网格个数的0.5倍。