可调谐超快激光贝塞尔光束加工方法研究(附MATLAB代码)
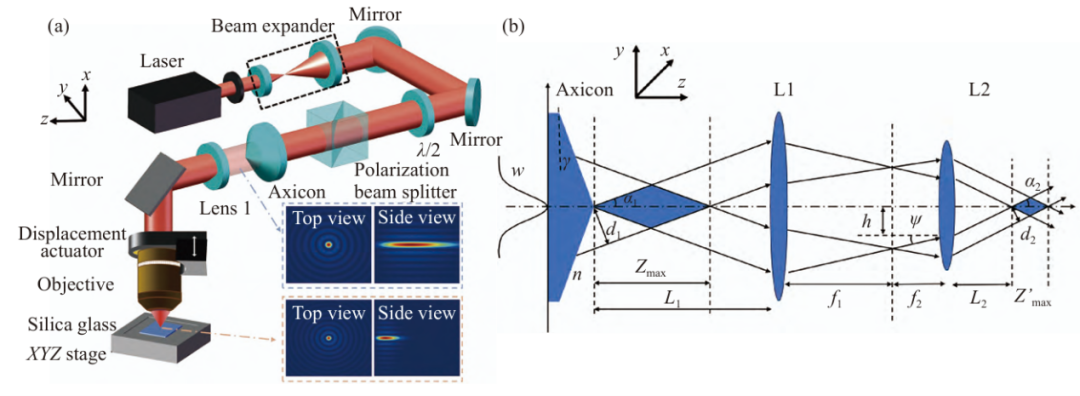
图1(a)可调谐超快激光贝塞尔光束加工系统示意图;(b)可调谐超快激光贝塞尔加工系统的几何光路图
一、 贝塞尔光束与超快激光加工背景
超快激光加工技术以其高精度、非接触、热影响区小等优势,已成为微器件制造的重要手段。然而,传统高斯光束聚焦后的焦深较短,对对焦精度提出极高要求,稍有离焦就可能导致加工失败或精度降低。与之相比,贝塞尔光束不仅具备较长的无衍射传输距离,还能有效拓展加工的动态范围,因此在高深径比微孔制备、激光切割、光波导写入等领域表现出极大优势。
二、贝塞尔光束的产生与调控原理
典型产生方法目前主流的贝塞尔光束生成方式包括环缝法、锥透镜法、计算机全息法、谐振腔法及球差透镜法。其中,锥透镜法因其结构简单、效率较高,被广泛应用于实际系统中。
可调谐系统设计文献提出了一套基于锥透镜与可调谐双远心光学系统的超快激光贝塞尔光束加工系统。系统的创新点在于,通过高分辨率闭环反馈控制的位移音圈致动器,灵活调节双远心系统压缩比,实现贝塞尔光束主瓣半径与无衍射距离的可控切换,从而适配不同样品与加工需求。
三、仿真分析——空间光场传播特性
理论模型以高斯光束入射锥透镜及不同压缩比的双远心系统为模型,对贝塞尔光束的空间分布进行理论推导。理论上,压缩比越大,所生成贝塞尔光束的中心主瓣半径越小,无衍射距离也随之缩短。
数值仿真通过数值模拟,文献系统分析了不同压缩比(如f1=250 mm, f2=36 mm,18 mm,9 mm)条件下,贝塞尔光束的主瓣半径及无衍射传输距离的变化:
·压缩比 f1/f2 =250/36 时,主瓣半径约3.73 μm,无衍射距离5.28 mm;
·压缩比为250/18时,主瓣半径约1.86 μm,无衍射距离1.32 mm;
·压缩比为250/9时,主瓣半径约0.93 μm,无衍射距离0.33 mm。
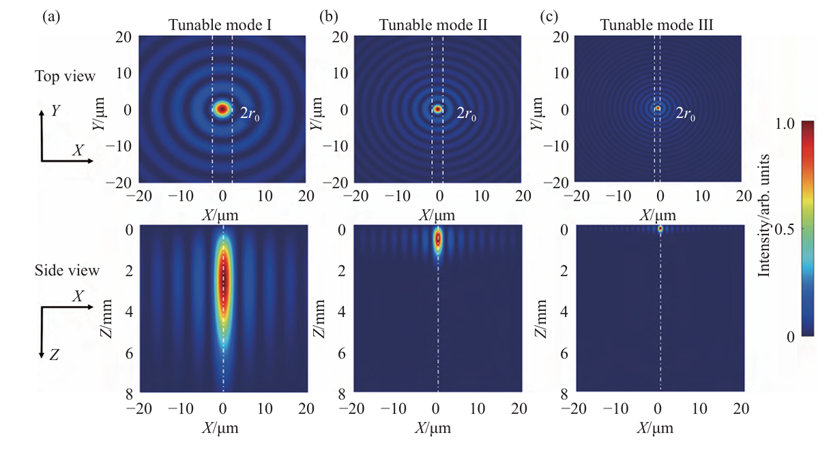
图2 不同调谐模式下产生贝塞尔光束的横截面和侧视图光强分布图。(a)可调谐模式Ⅰ;(b)可调谐模式Ⅱ;(c)可调谐模式Ⅲ
仿真结果揭示了系统调谐能力对光场分布的灵活控制,且为实验设计提供了理论基础。
光场分布可视化通过绘制横截面及轴向传播方向的强度分布图,可直观展示贝塞尔光束典型的“亮暗同心环”结构,主瓣能量集中,侧瓣能量分布均匀,且随传播距离变化空间分布几乎不变,充分体现了其无衍射特性。
四、实验验证
检测系统搭建自主搭建了贝塞尔光束检测实验装置,包括收集物镜、单透镜、光束质量分析仪及高精度位移导轨,能够实现对主瓣半径和无衍射距离的高精度测量。
实验结果对比实验测试在不同可调谐模式下获得的贝塞尔光束主瓣直径与无衍射距离:
·模式Ⅰ:主瓣直径131.15 μm(放大后),无衍射距离1620 mm,逆推到放大前为3.74 μm和5.289 mm;
·模式Ⅱ:主瓣直径65.68 μm(放大后),无衍射距离约330 mm,逆推为1.86 μm和1.32 mm;
·模式Ⅲ:主瓣直径32.84 μm(放大后),无衍射距离70 mm,逆推为0.93 μm和0.33 mm。
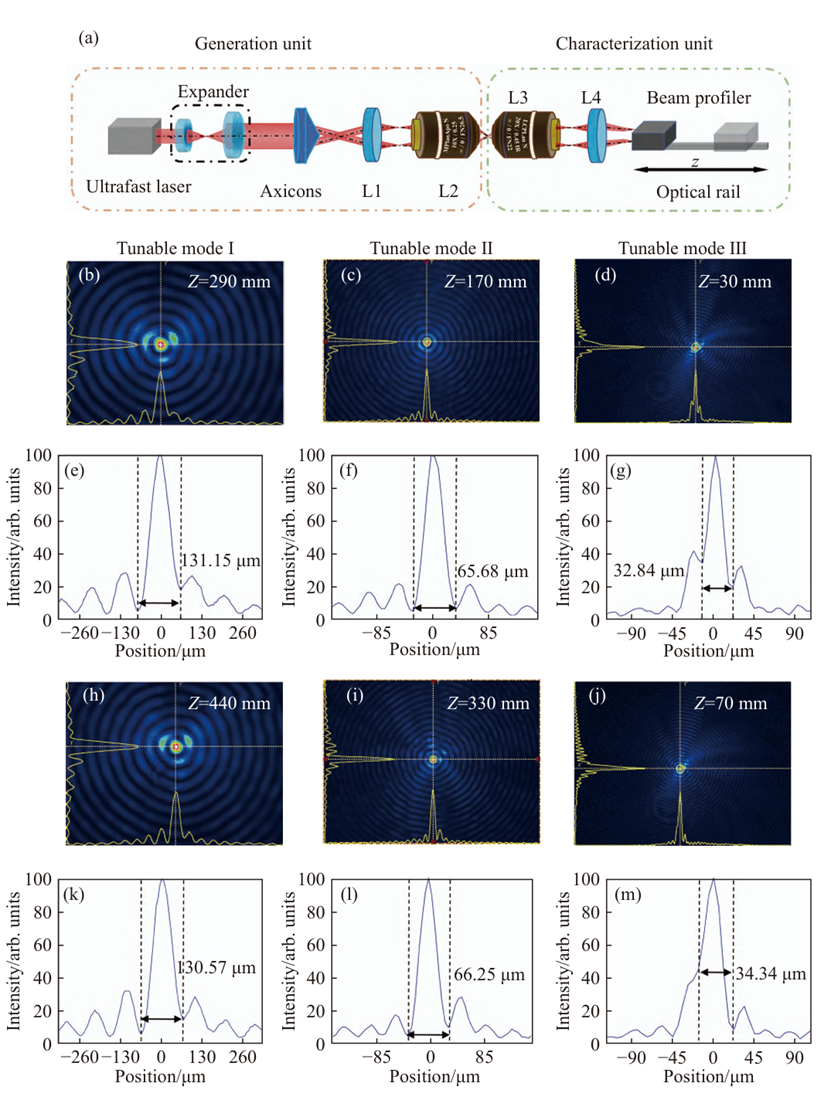
图3 (a)贝塞尔光束检测实验装置;(b)、(e)在可调谐模式Ⅰ条件下传输距离为290 mm时的贝塞尔光束横截面光强分布和截面光强曲线分布图;(h)、(k)传输距离为440 mm;(c)、(f)在可调谐模式Ⅱ条件下传输距离为170 mm时的贝塞尔光束横截面光强分布和截面光强曲线分布图;(i)、(l)传输距离为330 mm;(d)、(g)在可调谐模式Ⅲ条件下传输距离为30 mm时的贝塞尔光束横截面光强分布和截面光强曲线分布图;(j)、( m) 传输距离为70 mm
上述实验结果与理论仿真高度一致,进一步验证了系统设计的准确性和可调性。
五、微器件加工应用
基于所设计的贝塞尔光束系统,研究团队对1 mm厚熔融石英进行了微孔加工实验,结果表明该系统不仅具备高精度、高效率,还可灵活调节加工精度,满足多样化的微器件制造需求。
六、结语与展望
本文基于文献,系统梳理了可调谐超快激光贝塞尔光束加工方法的仿真与实验过程。仿真分析揭示了双远心系统压缩比对贝塞尔光束空间特性的精准调控机理,实验验证则进一步巩固了理论基础。未来,随着系统集成度和自动化水平的提升,贝塞尔光束有望在超快激光高精密微纳加工、光学通信、量子信息等领域展现更广阔的应用前景。
七、文献复现
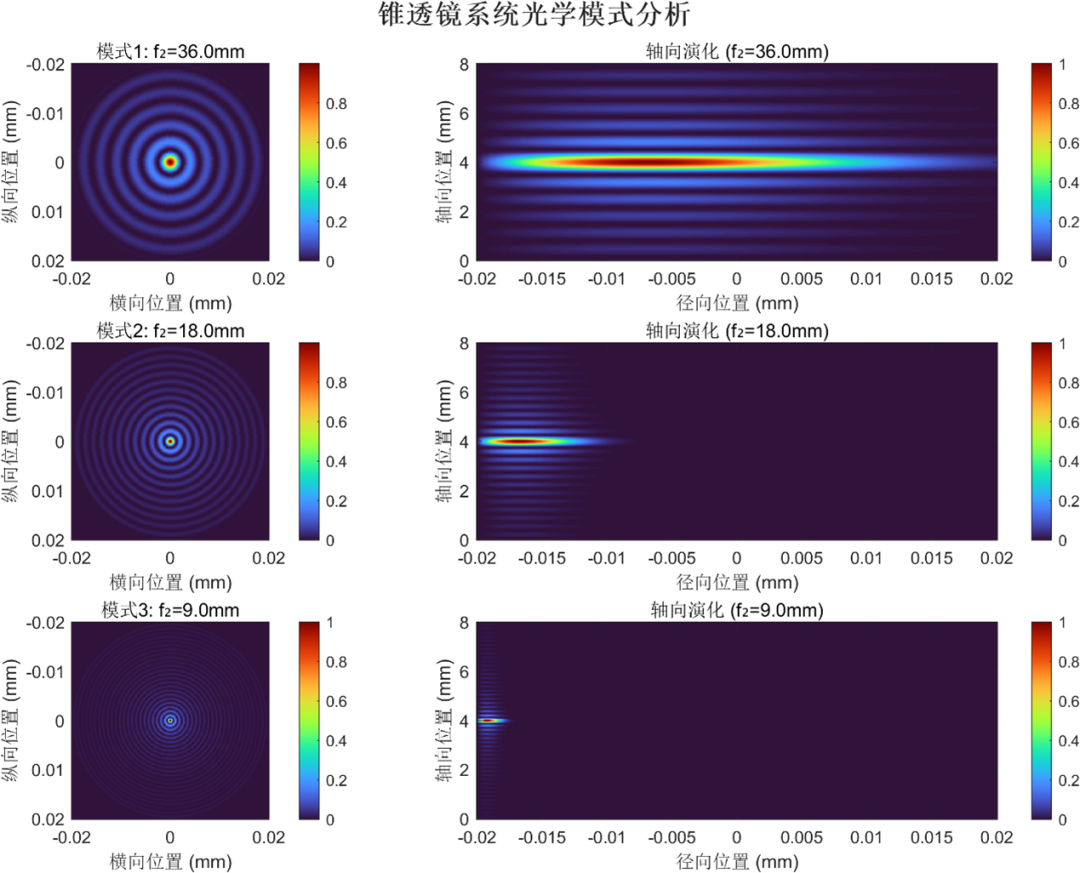
图4 仿真复现:不同调谐模式下产生贝塞尔光束的横截面和侧视图光强分布图
八、MATLAB代码
clear; clc;%% 系统参数gamma_degree = 2; % 锥透镜底角(度)beam_waist = 4e-3; % 入射光束半径(m)f_lens1 = 250e-3; % 透镜L1焦距(m)f_lens2_list = [36e-3, 18e-3, 9e-3]; % 透镜L2焦距列表refractive_index = 1.45; % 折射率(熔融石英)wavelength = 1064e-9; % 波长(m)intensity_peak = 1; % 归一化光强%% 坐标参数设置radial_points = linspace(-0.02e-3, 0.02e-3, 300); % 径向坐标axial_points = linspace(0, 8e-3, 300); % 轴向坐标%% 参数准备params = struct(...'gamma_rad', deg2rad(gamma_degree), ...'beam_waist', beam_waist, ...'f_lens1', f_lens1, ...'refractive_index', refractive_index, ...'wavelength', wavelength, ...'intensity_peak', intensity_peak ...);%% 创建紧凑布局的静态图像fig_static = figure('Position', [100 100 1000 700], 'Color', 'w', 'Name', '静态分析');colormap(turbo);tiledlayout(3, 2, 'TileSpacing', 'tight','Padding', 'compact');% 计算并绘制三种模式for mode_idx = 1:3f_lens2 = f_lens2_list(mode_idx);result = computeBesselBeamProfile(params, f_lens2, radial_points, axial_points);% 二维径向分布nexttile;imagesc(result.radial_points*1e3, result.radial_points*1e3, result.intensity_2D');axis image;xlabel('横向位置 (mm)');ylabel('纵向位置 (mm)');title(sprintf('模式%d: f₂=%.1fmm', mode_idx, result.f_lens2*1e3));colorbar;set(gca, 'FontSize', 10);% 轴向演化分布nexttile;imagesc(result.radial_points*1e3, result.axial_points*1e3, result.intensity_normalized');axis tight;xlabel('径向位置 (mm)');ylabel('轴向位置 (mm)');title(sprintf('轴向演化 (f₂=%.1fmm)', result.f_lens2*1e3));colorbar;set(gca, 'FontSize', 10, 'YDir', 'normal');endsgtitle('锥透镜系统光学模式分析','FontSize', 16, 'FontWeight','bold');%% 保存静态图像exportgraphics(fig_static, 'optical_modes_analysis.png', 'Resolution', 300);savefig(fig_static, 'optical_modes_analysis.fig');disp('静态分析图像已保存为 optical_modes_analysis.png 和 .fig 文件');
九、参考文献
[1]全宏升,马威峰,唐赞,张宗全,金昌骏,邱丽荣,徐可米,赵维谦.可调谐超快激光贝塞尔光束加工方法研究[J].红外与激光工程, 2024(8):56-64.
[2] KUANG Z, PERRIE W, LIU D, et al. Ultrafast laser parallel microprocessing using high uniformity binary Dammann grating generated beam array [J]. Appl Surf Sci, 2013, 273: 101-106.
[3] LIU H, LIN W, HONG M. Hybrid laser precision engineering of transparent hard materials: challenges, solutions and applications [J]. Light: Science & Applications, 2021, 10(1): 162.





