Σ-Δ调制器的原理及在锁相环的应用

锁相环（PLL）是射频系统的核心。其核心目标在于使压控振荡器（VCO）的输出信号与参考信号在频率和相位上精确锁定。

一、频率分辨率与相位噪声的权衡

以整数N分频锁相环为例： 输出频率 F_out = N * F_ref（N 为整数分频比）。其频率分辨率等于参考频率 F_ref。要获得精细的频率步进（高分辨率），必须降低 F_ref。但过低的 F_ref 会导致环路带宽变窄，使得：

抑制VCO相位噪声的能力下降（环路无法有效滤除VCO自身高频噪声）。

锁定速度变慢。

在分辨率和参考频率上的折中引入了小数分频锁相环： 引入分数分频比概念：F_out = (N + F) * F_ref（F 是小数部分，0 ≤ F < 1）。理论上，它能在保持较高 F_ref（利于抑制噪声和快速锁定）的同时，实现任意精细的频率分辨率（F_ref 的分数倍）。

小数分频不可规避的问题小数杂散： 实现分数分频比最常见的方法是让分频器在 N 和 N+1 之间动态切换 。例如，要平均分频比 N10.1，需在11个参考周期内进行10次N分频和1次N+1分频。这种周期性 的分频比切换，会直接调制 VCO的输出相位，在输出频谱上产生以 F * F_ref 及其谐波为中心的严重杂散（分数杂散），其能量远高于宽带相位噪声，破坏频谱纯度和信号完整性。

二、 Σ-Δ调制器

Σ-Δ调制器（SDM）的核心在于将量化噪声能量从低频信号带内推（整形）到高频区域。

基本原理：

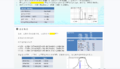
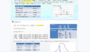
Σ-Δ调制器是一种过采样架构，因此，我们从奈奎斯特采样理论和方案以及过采样讨论。假设采样以标准奈奎斯特方式运行。这种情况下，量化噪声由ADC的LSB大小决定。FS为ADC的采样速率，FS/2为奈奎斯特频率。当它以过采样方式运行，采样速率更快。采样速率提高K倍，量化噪声扩展到K × FS/2的带宽上。

Σ-Δ调制器是一种负反馈系统，根据传递函数可以推导出一下公式。信号传递函数用作一个低通滤波。噪声传递函数是一个高通滤波器函数，提供噪声整形，在DC附近的较低频率，对量化噪声有很强的抑制。

所以Σ-Δ调制器多了一个特性，那就是噪声整形，如图所示。模数转换的量化噪声被调制整形，从低频移动到较高频率，低通数字滤波器可将其从转换结果中消除。Σ-Δ型ADC的噪底由热噪声决定，而不受量化噪声的限制。

三、Σ-Δ调制器与锁相环

Σ-Δ调制器作为分数分频控制器：

输入：目标分数部分 F。

输出：高速的 0/1 比特流（或低位数码流）。

 SDM 动态控制分频器在 N 和 N+1 之间切换。它不是 简单地按 F 的比例周期性切换（这会产生强杂散），而是以一种高频、随机化、受控 的方式切换。这种切换序列的平均值精确等于目标分数 F。

噪声整形作用于相位误差：

分频比的切换(N -> N+1)直接导致相位检测器（PFD/CP）输入端的相位跃变（误差）。

类比量化误差： 这种由分频比切换引入的相位阶跃误差（ΔΦ = 2π * (ΔN)，ΔN 是 0 或 1），其频谱特性与SDM输出的频谱特性一致。

SDM的贡献： SDM 的噪声整形功能（高通特性 NTF(z)）意味着其输出序列的低频分量（能量）被极度抑制 。因此，由其控制的、分频比切换造成的相位误差中的低频分量也同时被强烈抑制 。

PLL环路滤波器的配合：

PLL环路本身是一个低通滤波器（从参考输入到VCO输出）。

SDM整形后的相位误差（表现为高频噪声）被PLL环路低通滤波器自然滤除。

最终效果： 原本集中在低频 F * F_ref 及其谐波处的强分数杂散 ，被SDM整形并推高到远高于PLL环路带宽的频率区域，随后被环路滤波器有效滤除 。在PLL输出频谱上，目标频率 F_out 附近原本的杂散尖峰消失了，取而代之的是抬升的宽带量化（相位）噪声基底 。

代价与优化： 这种方案的代价是输出相位噪声基底在高频区域有所抬升。

与传统的模拟补偿方法相比，Σ-Δ调制器采用数字技术，具有最小的附加相位噪声，并且能够将小数杂散降低到更低的水平。

通过以上方式，Σ-Δ调制器在锁相环中发挥了重要作用，有效降低了杂散信号，提高了信号的质量和系统性能。