Ansys Workbench随机振动分析
很多工程情况下,载荷是不确定、杂乱无章的,无法获得每一时刻的载荷条件,如火箭每次发射会产生不同时间历程的振动载荷,汽车在路上行驶每次的振动载荷也会有所不同。由于振动载荷时间历程的随机不确定性,所以不能选择瞬态分析进行模拟计算。
随机振动分析可以评估结构在随机载荷激励下的振动响应特性,它考虑了结构的固有振动特性和随机激励之间的相互作用,帮助我们理解系统在随机环境下的工作情况。本文以某型号太空望远镜为例,详细讲解Ansys Workbench随机振动分析流程,步骤如下所述。
1 构建几何模型
在Solidworks环境下,构建太空望远镜几何模型,如下图所示。点击菜单栏中的“工具“,选择Ansys Workbench,将几何模型传输至Ansys Workbench的Germetry中。
2 创建分析流程
进入Workbench界面后,设置Units为mm,依次拖拉Modal和Radom Vibration,创建模态叠加法随机响应分析流程,如下图所示。点击File,选择Save,保存分析项目。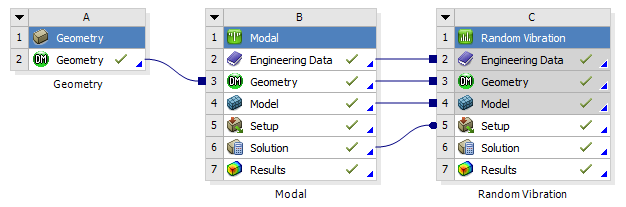
Ansys Workbench随机振动分析项目流程图3 生成几何模型
右击Geomrtry,选择Edit Geometry in DesignModeler....,进入DM界面。菜单栏点击Units,设置单位为Millmeter(mm)。右击Attacxh1,选择Generate生成几何模型。4 添加材料属性
关闭DM界面,返回Workbench流程界面。双击Engineering Data,右击空白处选择Engineering Data Sources,点击General Materials,添加所需材料,如下图所示。
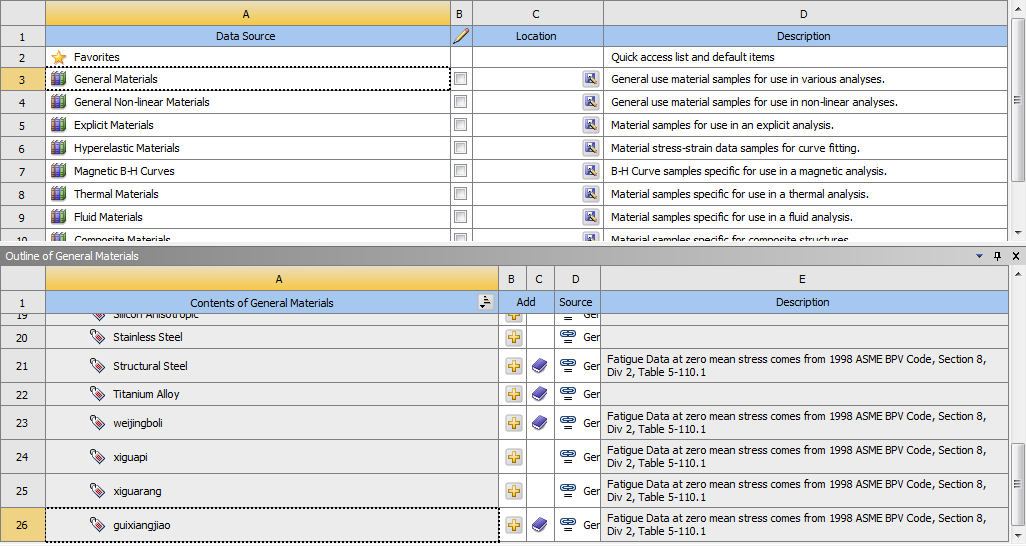
添加材料属性
5 设置单元特性
双击Modal中的Model,进入Mechanical界面。展开Generoty,逐个单击几何模型,并在下方列表的Assignment中选择对应材料,其余保持默认设置,如下图所示。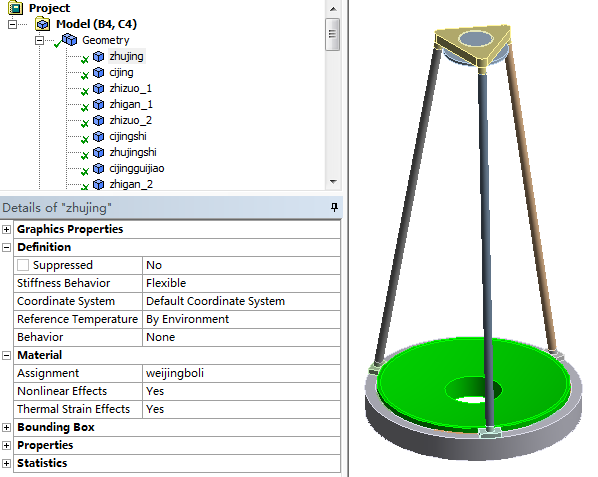
展开Connections,点击Contacts,设置Tolerance Type为Value(Value为0.1),右击Contacts,选择Create Automatic Connections,生成若干绑定接触对,如下图所示。
设置接触关系
6 约束模态分析
采用模态叠加法进行随机振动分析,因此首先进行模态分析,以确定频率范围、模态数量和振型信息。此外,为使约束点输入激励与试验条件保持一致,采用大质量法进行随机振动分析。参加前期文章:Ansys Workbench动力学分析中的大质量法。
点击Geometry,添加Point Masst,选择安装面,点击Apply,输入质量Mass等。右击Point Mass,选择Promote to Remote Point,模型树中出现Remote Points,展开后下方出现Point Mass-Remote Point,如下图所示。
右击Modal,添加远端约束Remote Displacement,下方列表中设置Scoping Method为Remote Point,Remote Points选择上述创建的远程点Point Mass-Remote Point,约束全部自由度为0,如下图所示。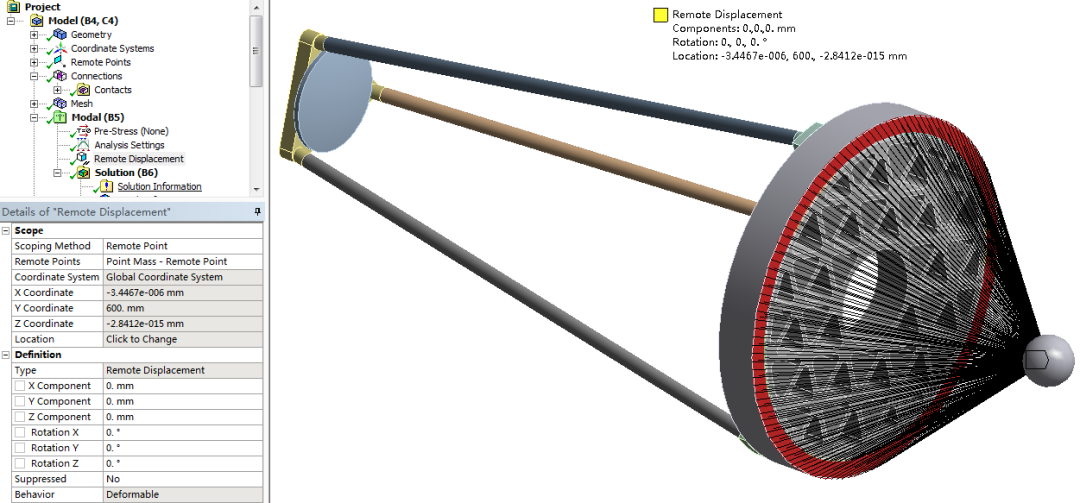
展开Modal,点击Analysis Settings,在Max Modes to Find中修改模态数量(本文取前20阶模态,实际工程按需选择),获取大于随机振动试验条件最大频率1.5倍的固有频率,保证所截取的模态有效质量分数≥90%,其余保持默认设置,如下图所示。
右击模型树Modal中的Solution,选择Solve求解。计算完成后,依次添加各阶总体变形(total),右击Solution,选择Equivalent All Results。单击Total Deformation,查看固有频率和振型。其中,某型号太空望远镜第一阶模态振型如下图所示。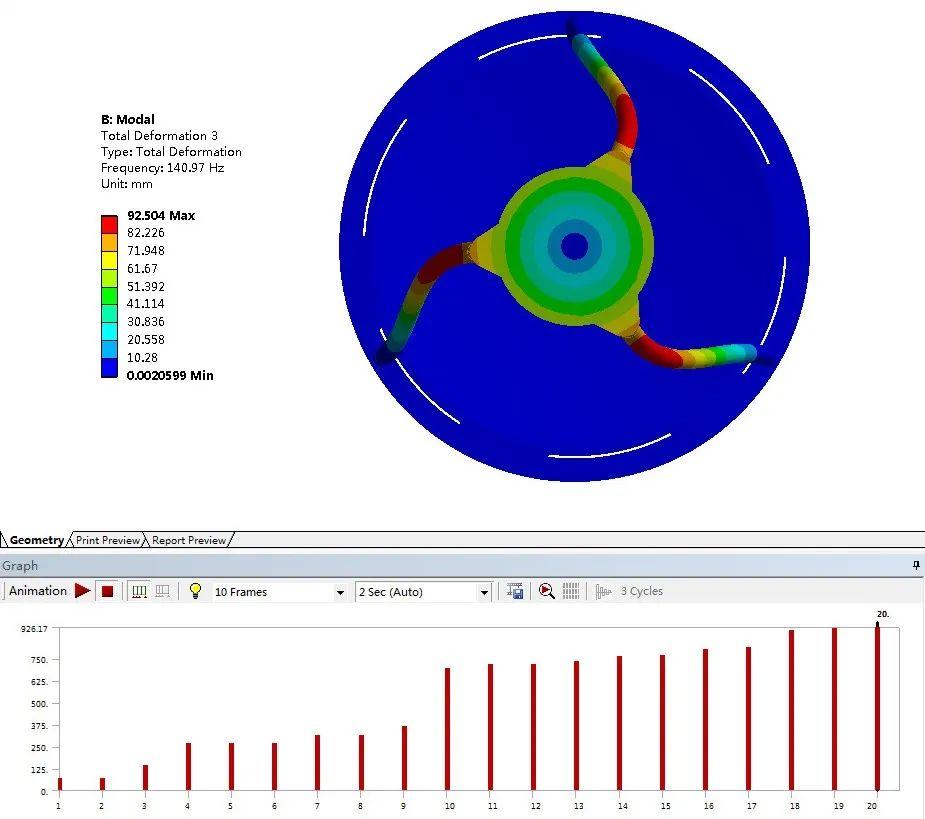
7 随机响应分析
通常用PSD(功率谱密度)激励来模拟结构所处的随机振动环境,Ansys Workbench中的PSD激励有四种:PSD Acceleration(加速度功率谱密度)、PSD Velocity(速度功率谱密度)、PSD G Acceleration(以重力加速度表示的功率谱密度)、PSD Displacement(位移功率谱密度)。PSD激励分类
点击模型树中的Random Vibration ,展开Environment中的RS Base Excitation,添加以重力加速度表示的功率谱密度PSD G Acceleration,设置基础激励Boundary Condition为Remote Displacement,设置Load Data和Direction,如下图所示。设置PSD激励
特别注意:Ansys Workbench会自动判断所输入的PSD数据是否合理,在Graph中显示的PSD曲线,最好是所有段均为绿色。如果曲线中有黄色段,可在相应的地方插入分段,即可变为绿色。
单击Analysis Settings,设置Number Of Modes To Use为All(具体按工程需要酌情考虑选取)、Calculate Velocity为Yes、Calculate Acceleration为Yes、常值阻尼比Constant Damping Ratio为0.03(阻尼系数,一般是试验得到,设为1%-4%)。分析设置
右击Solution,依次添加位移Directional、加速度Directional Acceleration、等效应力Equivalent Stress等,并在下方面板中设置Geometry为All Bodies(或单个结构件),Scale Factor为3 Sigma,Orientation与激励方向保持一致,其余保持默认。
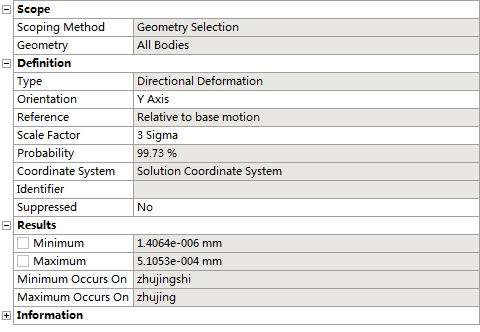
添加分析结果
其中,1 sigma、2 sigma和3 sigma是标准差(Standard Deviation)的倍数,用于描述结果的统计偏差范围的术语,可以帮助工程师评估结构在随机振动环境下的可靠性和安全性。通常情况下,较大的sigma范围表示结果具有更大的离散程度和不确定性。
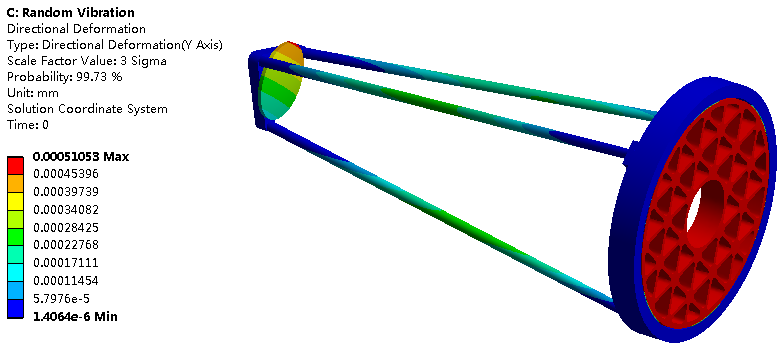
右击Solution,添加Response PSD Tool,图形区选择节点并点击Apply,下方面板中设置Reference为Absolute、Result Type为Acceleration、Result Selection与载荷激励方向一致、Acceleration in G为Yes,其余保持默认设置,如下图所示。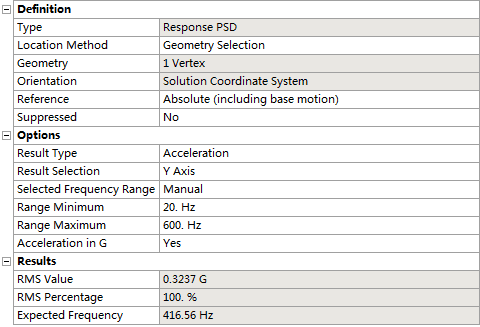
右击Solution,选择Equivalent All Results求解。计算完成后,分别查看望远镜或组部件的位移响应云图、应力响应云图和加速度响应云图。同时,查看不同节点(主镜、次镜、支撑杆等)处的加速度响应功率谱密度随频率变化情况,如下图所示。