建筑和制造中的材料添加和去除
与此相反的是在物理、化学或其他加工过程中去除材料。用于去除材料的技术会产生热量,热量会传递到剩余的材料上。由此产生的热膨胀可能会导致暂时和永久的变形。并且,要去除的材料量应考虑零件的最终收缩和可能的变形。
如何使用 Abaqus 虚拟评估和优化材料添加和去除
状态的改变允许元素在一个步骤内被停用或激活,而场变量可用于改变材料属性以模拟移除或添加的效果。当需要逐渐增加或减少刚度而不是状态的瞬时变化时,场变量可能是有利的。这些程序可以独立或串联应用以达到所需的结果。渐进式元素激活是一种保真度较高的方法,允许完全和部分元素激活。有关此方法的更多信息可以在 Abaqus 文档中找到。
模型设置
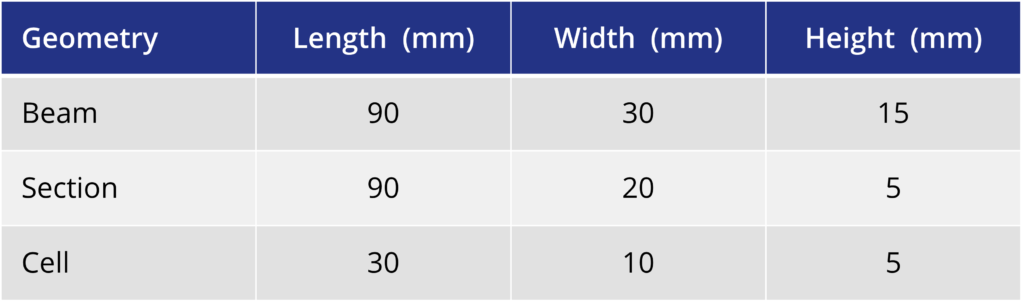

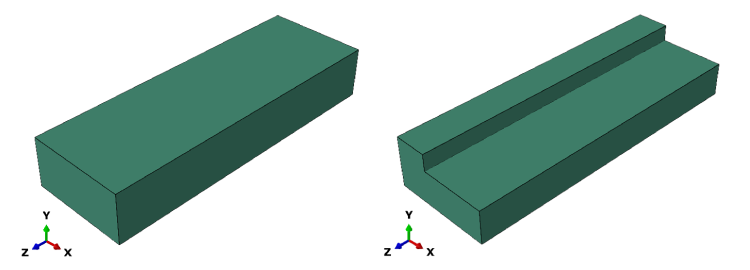
图 1:初始和最终几何形状
无论选择哪种方法,此过程的第一步都是对几何结构进行分区,以确定要移除的单元格。零件几何形状应反映最大尺寸 - 如果材料被去除,这将反映初始几何形状;如果添加材料,这将反映最终的几何形状。通过划分部分,可以将各个组分配给要删除的单元。
对于此示例,零件几何形状被划分为 3 × 3 × 4 单元,如图 2 所示。然后根据零件级别的几何形状将集 合分配给各个单元。当需要重新网格化并且在装配体中以partname-instance.setname 的形式访问这些集时,此方法非常可靠。这里,这些组是根据它们在零件形式X1-Y1-Z1到X3-Y3-Z4中的 x、y、z 位置来命名的 - 后面的零件在图 2 中突出显示。零件名称为Part-1,第一个零件为 Part-1。并且该部分的唯一实例被标记为Part-1-1 。随后,集 合X3-Y3-Z4在装配级别被识别为Part-1-1.X3-Y3-Z4 。
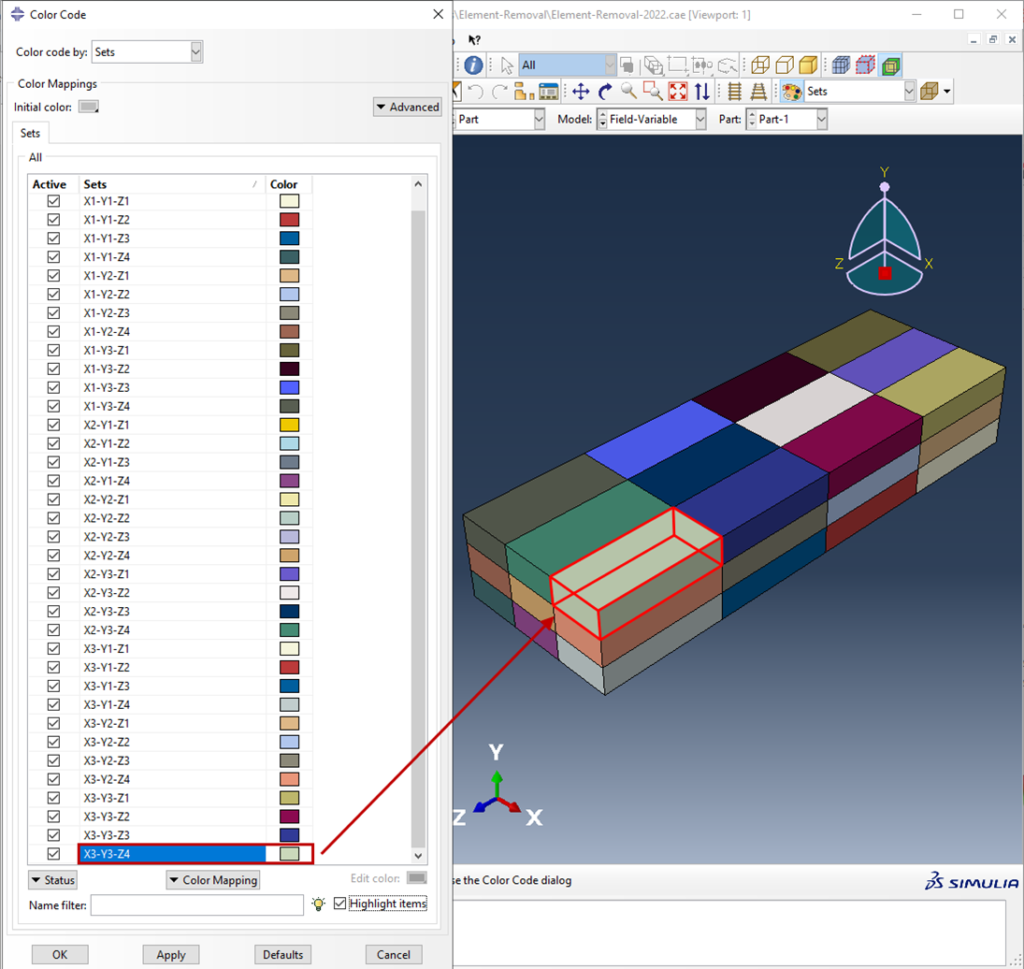
关键字编辑
场变量的空间变化用于引发局部材料降解,以及随后的材料去除或添加的效果。材料属性的编写依赖于指定的字段变量。温度依赖性是该通用框架的一个具体示例。通过在步骤内更改字段变量的值,属性会在模拟内的指定时间发生更改。振幅与所需组的场变量相关联,以管理空间变化,并随后控制哪些单元受到材料属性变化的影响。在此示例中,杨氏模量和泊松比降级到对模型内八个单元的零件刚度影响可以忽略不计的程度。
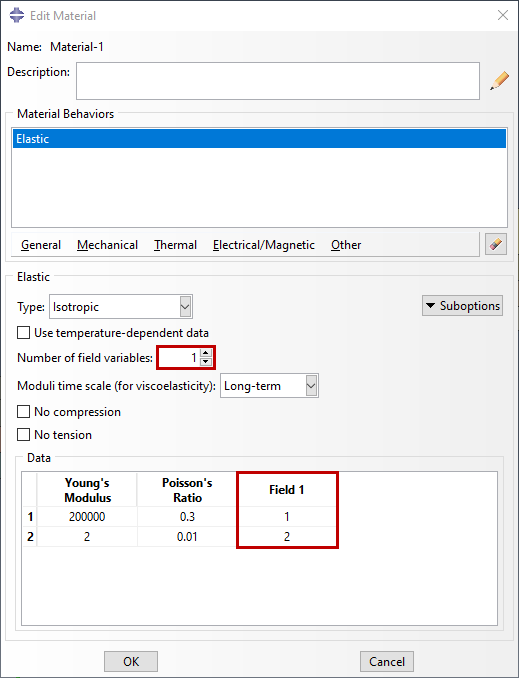
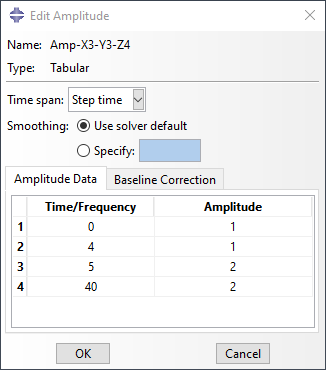
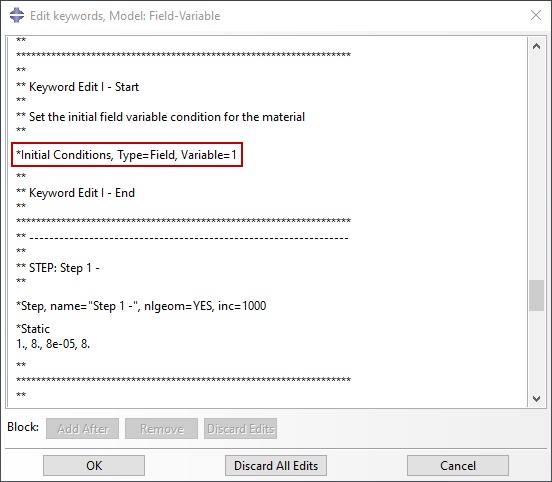
在所需的步骤中,根据基于时间的幅度更改场变量。这里,幅度函数Amp-X3-Y3-Z4与装配级别和场变量 1 上的Part-1-1.X3-Y3-Z4集相链接,如图 6 所示。
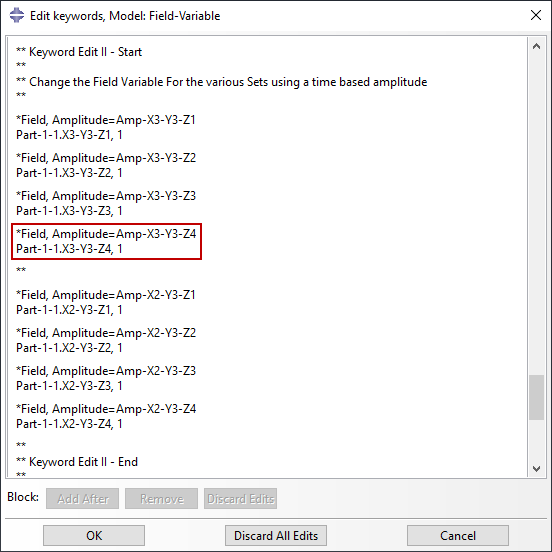
型号变更
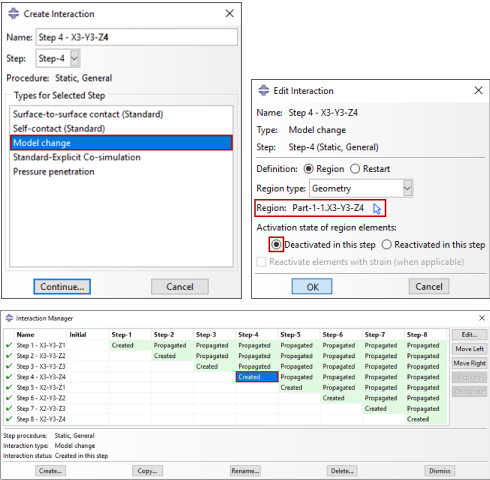
边界条件:静态应力分析中材料的去除。确保模型的其余部分受到充分约束以防止出现无约束刚体模式非常重要。 载荷:在元件被移除或重新激活的区域施加的分布式和集中载荷可能需要修改。 元件:目前不适用于刚性元件、粘性元件、垫圈元件和压电元件。可以删除和重新激活 Abaqus/Standard 中的所有其他元素类型。 接触:如果连接到接触对的元件被移除,则在启动模型更改时应移除或停用接触对。 约束:如果要删除附加到受多点约束或线性约束方程约束的节点的所有元素,则该节点应为多点约束或线性约束方程的从属节点。 警告:在某些情况下,元素删除可能会导致 Abaqus/Standard 在消息文件中报告额外的未连接区域。忽略这些消息是安全的。





