服务:
- 90天知识圈
- 在线开票
- 提供培训通知
- 交流群
本课适合哪些人学习:
1、学习仿真工程师;
2、学习优化方法工程师;
3、拓扑优化学习和应用者;
4、从事传热设计和优化的工程师;
5、电子散热、储能工程师。
你会得到什么:
1、学习拓扑优化计算流程
2、帮助学员掌握传热仿真计算;
3、能帮助用户掌握拓扑优化设计方法,提升优化设计能力;
4、能够解决传热效率提升问题。
课程介绍:
一、流热耦合拓扑优化技术原理
利用变密度方法进行拓扑优化设计的思想是:在一个由伪密度表征的连续体设计域中,每个设计单元的密度值γ 均可以取(0—1)区间中任何数值,以伪密度值为设计变量,在满足约束函数G1 的条件下,不断趋近目标函数值J 的最大值或者最小值,直到满足收敛条件。表达式如下:
其中s 为相应物理量的状态变量,G1 为流体体积分数的约束函数,Vf 为流体体积分数。其中黑色表示为固体域,γ=0,α→∞,f→∞;白色表示为流体域,γ=1,α→0,f→0。f为体积力
二、拓扑优化中传热问题
(1)在动量方程中添加阻力项表示流体流经设计域时受到的阻力;
(2)设计域中的材料密度表示为设计变量γ,当设计变量γ 等于0 时,表示设计单元内充满流体材料,当设计变量γ 等于1 时,表示设计单元内充满固体材料;
(3)流体和固体的材料物性参数均为定值,设计域内的材料属性通过单元材料密度进行插值;
其中,p 为压力,u=[ux,uy]T 为x,y 方向的流速,ρ 为材料的密度,T 为温度,μ 为动力粘度,cp 为定压比热容,k 为热传导系数:
体积力 f=α∙u
其中f 为设计域内的体积力,α 为阻流系数:
其中q 为惩罚因子,αmax 与雷诺数和达西数有关系。
当γ=0 时,设计域内为流体材料,体积力项f=0,对流速不进行惩罚;当γ=1 时,表示设计域内为固体材料,体积力趋近于无穷大,流速被惩罚至零.
能量方程
其中Q 为热源,用牛顿冷却公式的方式表达,这里h 是根据温差控制产生热量的等效传热系数。
为了获得更加清晰的拓扑形态构型图,普朗特数Pr 取6.78。达西数取值越大代表多孔
介质材料的渗透度能力越强,达西数Da取值为10-4。
三、拓扑优化
插值、过滤及投影
在设计域中设计变量与材料属性之间构建函数关系进而控制每个设计单元。
其中下标s 代表固体,下标f 代表流体。液体的流动阻力f 为0,固体的流动阻力αs 由特征长度L 和达西数Da 决定:
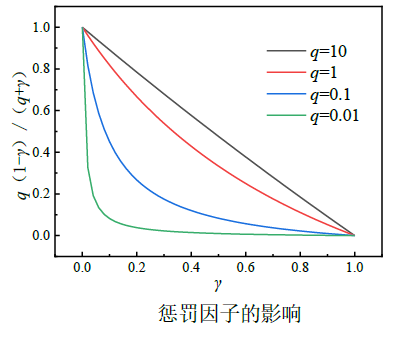
惩罚因子q 对材料插值模型的有影响,设计变量γ 的取值范围为(0-1)之间的任意值,通过惩罚因子的惩罚作用使趋近于中间的密度值进一步向(0-1)两端靠近,这样连续变量的拓扑优化模型可以更好的趋近于原来的(0-1)分布状态,建议q 取值为0.01。
在拓扑优化过程中,为避免产生的网格敏感性问题,需加入密度过滤的方法。另一方面,在流体传热的拓扑优化问题中,密度过滤方法可以有效避免优化问题中的不适定性。采用亥姆赫兹偏微分方程(PDE)形式的密度过滤方法,表达式如下:
γ 表示为未经过滤的设计变量,𝛾̃表示为已过滤后的设计变量,r 为过滤半径。
利用上述密度过滤方法虽然可以提高数值稳定性,但是会导致大量灰度单元的产生,
为了解决此问题,引入双曲正切投影方法,以获得更加清晰的拓扑流道形态.
其中,𝛾̂为投影后的设计变量,γβ 为投影点,投影点取值为0.5。过滤后的结果如图所示。为避免在优化过程中陷入局部最优解问题,采用连续变化方法:β 表示投影斜率,取值大小表示其结果的清晰程度。随着β 值的逐步增大,使得流固边界更加清晰,β 取值为8或其倍数。
四、多目标拓扑优化
双目标函数归一化来寻找流体拓扑优化设计形状
目标函数及约束条件
在流体的优化设计中,增强换热性能与降低流动阻力是相互矛盾的,要解决此问题,利用双目标函数加权方法。采用换热量最大化Jth 与流体总势能Jf 两个目标函数,并对二者进行归一化处理。同时引入目标函数的权重系数ω 构成拓扑优化总目标函数J,表示为:
在设计域内将进出口总压降定义为流体体积内的总势能:
对以上两个目标函数进行归一化
其中,Jth’与Jf’分别为归一化处理后的换热性能和流体总势能的目标函数,Jth,max 与Jth,min代换热性能达到最大化或最小值时所取的值,Jthmax 与Jthmin,代表流体总势能达到最大化与最小化时所取的值。将两个目标函数线性组合构成多目标优化问题,表示方法如下:
液冷板流体拓扑优化
优化几何有两种
同侧进出口
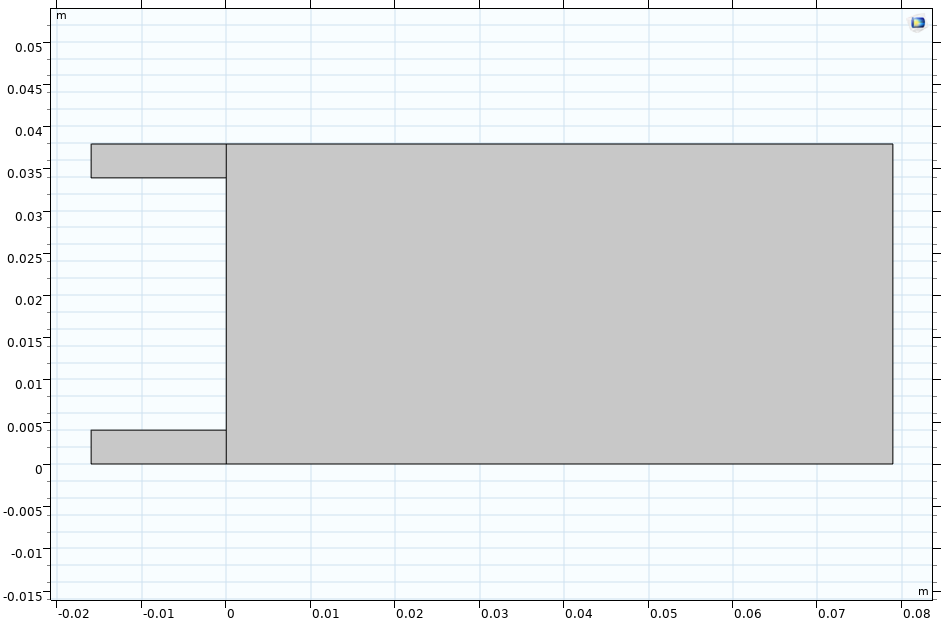
对侧出口
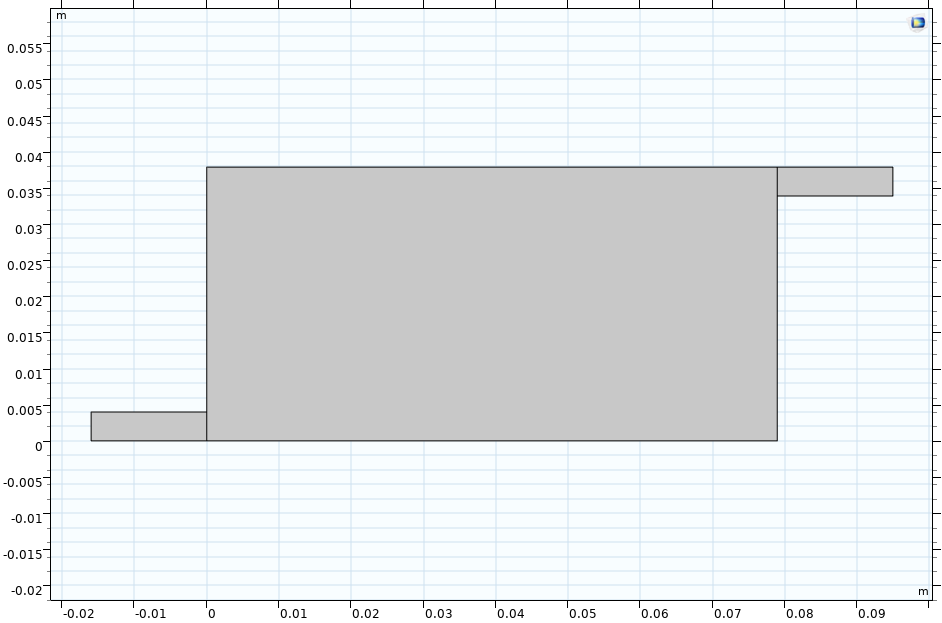
双优化目标:1.最大换热系数 最小流阻
2.最小平均温度 最小流阻
最大换热系数
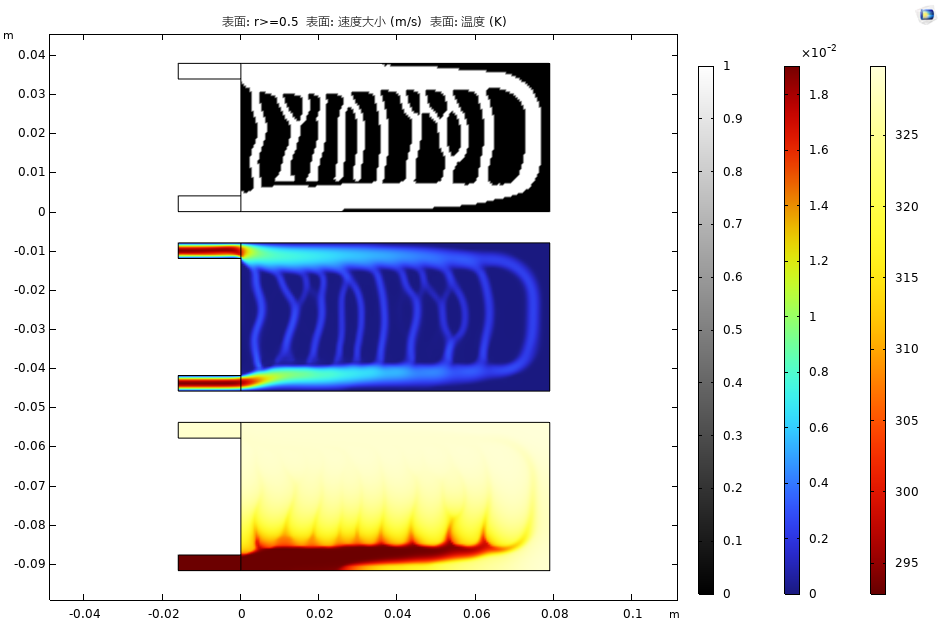
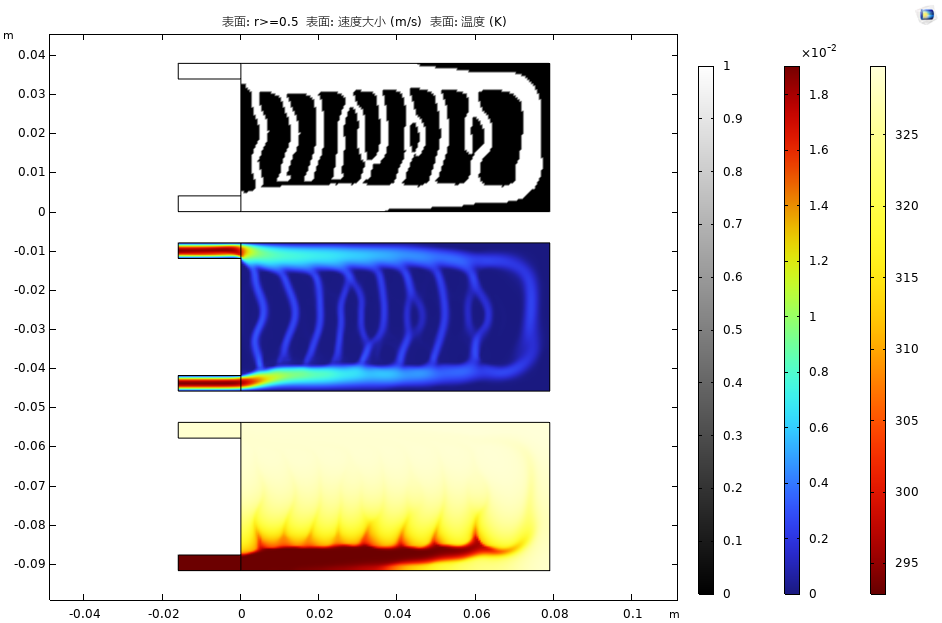
最小平均温度
对侧出口
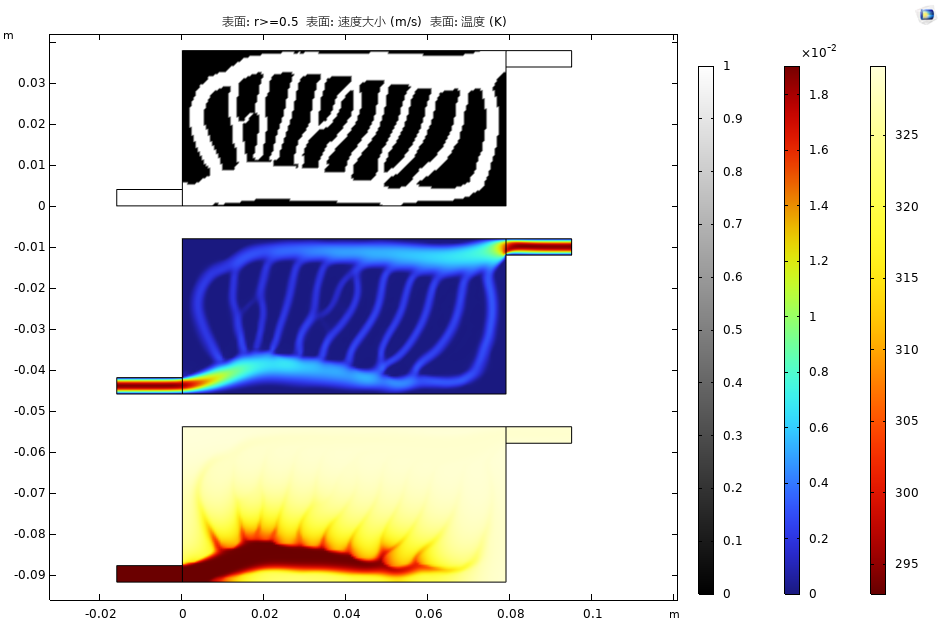
对侧出口提升和优化效果
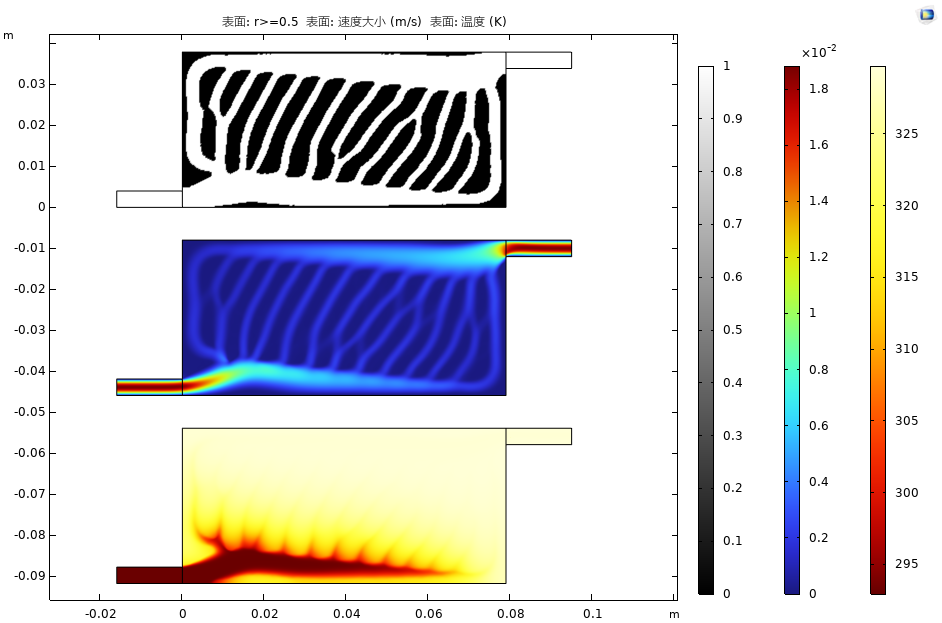
课程相关图片: